NOIP2024模拟2

合集 - 高一上七月(23)

1.高一上七月上旬日记2024-07-012.牛客周赛 Round 492024-07-013.Denso Create Programming Contest 2024（AtCoder Beginner Contest 361）2024-07-074.NOIP2024模拟12024-07-08

5.NOIP2024模拟22024-07-10

6.高一上七月中旬日记2024-07-117.NOIP2024模拟32024-07-118.CSP提高组模拟12024-07-129.暑假集训CSP提高模拟12024-07-1810.暑假集训CSP提高模拟22024-07-1911.暑假集训CSP提高模拟32024-07-2012.暑假集训CSP提高模拟42024-07-2113.高一上七月下旬日记2024-07-2214.暑假集训 加赛12024-07-2215.暑假集训CSP提高模拟52024-07-2316.暑假集训CSP提高模拟62024-07-2417.加赛22024-07-2418.暑假集训CSP提高模拟72024-07-2519.暑假集训CSP提高模拟82024-07-2620.暑假集训CSP提高模拟92024-07-2721.暑假集训CSP提高模拟102024-07-2822.暑假集训CSP提高模拟112024-07-2923.暑假集训CSP提高模拟122024-07-31

收起

NOIP2024模拟2

$T1$ GHzoj 3731. 酸碱度中和 $AC$

• 显然属性值具有单调性，考虑二分答案，设其分出的答案为 $mid$ 。

• 对于第 $i$ 瓶盐水，其覆盖的范围为 $[a_i-mid,a_i+mid]$ 。然后问题就转化成了区间选点问题，排序（因为不会存在除重合区间内只有一个端点相同的区间，胡乱排一下就行）后贪心地选取左端点即可。

  点击查看代码

  ll a[100010],l[100010],r[100010];
  bool check(ll mid,ll n,ll k)
  {
      ll sum=0,pos=0;
      for(ll i=1;i<=n;i++)
      {
          l[i]=a[i]-mid;
          r[i]=a[i]+mid;
      }
      for(ll i=n;i>=1;i--)
      {
          if(l[i]<=pos&&pos<=r[i])
          {
              continue;  
          }
          else
          {
              sum++;
              pos=l[i];
          }
      }
      return sum<=k;
  }
  int main()
  {
      ll n,k,l=0,r=0,mid,ans=0,i;
      cin>>n>>k;
      for(i=1;i<=n;i++)
      {
          cin>>a[i];
      }
      sort(a+1,a+1+n);
      r=a[n];
      while(l<=r)
      {
          mid=(l+r)/2;
          if(check(mid,n,k)==true)
          {
              ans=mid;
              r=mid-1;
          }
          else
          {
              l=mid+1;
          }
      }
      cout<<ans<<endl;
      return 0;
  }
  

$T2$ GHzoj 3732. 聪明的小明

• 部分分

  

  • $5pts$ ：区间重叠部分恰好等于 $k-1$ 说明第 $i(i>k)$ 瓶酒和第 $i-k$ 瓶酒的种类是一样的。种类数为 $A_k^k=k!$ 。

  

• 正解

  • 观察到 $1\le m\le k\le 10$ 和 $1024MB$ 的内存，考虑进行状压。
  • 对于一段区间 $[l,r]$ 在继续转移的过程中只有每种酒最后出现的位置是有用的，即我们可以只保存每种酒最后出现的位置。而其具体每个位置是什么并不重要，故可以用 $0/1$ 表示这个位置不是/是某种酒最后出现的位置。
  • 设 $f_{i,s}$ 表示以 $[i-m+1,i]$ 内每个位置的状态为 $s$ 时的方案数。填表法有点难写，考虑刷表，有 $f_{i+1,s^{\prime }}+=f_{i,s}$ ，其中 $s^{\prime }$ 是 $s$ 下一位能转移的状态。
  • 边界 $f_{m,s}$ 需要特殊处理，具体地，从右往左枚举 $s$ 的每一位，设先前已经枚举了的 $1$ 的个数为 $cnt$ ，若当前位为 $1$ 则对答案产生的贡献为 $k-cnt$ ，否则对答案的贡献为 $cnt$ 。
  • 最终，有 $\sum f_{n,s}$ 即为所求。
  点击查看代码

  const ll p=998244353;
  ll f[100010][(1<<10)+10];
  vector<ll>s;//卡常用
  int main()
  {
  	ll n,k,m,ans=0,cnt,i,j,h;
  	cin>>n>>k>>m;
  	for(i=0;i<=(1<<m)-1;i++)
  	{
  		if(__builtin_popcount(i)==k)
  		{
  			s.push_back(i);
  			cnt=0;
  			f[m][i]=1;
  			for(j=0;j<=m-1;j++)
  			{
  				if((i>>j)&1)
  				{
  					f[m][i]=f[m][i]*(k-cnt)%p;
  					cnt++;
  				}
  				else
  				{
  					f[m][i]=f[m][i]*cnt%p;
  				}
  			}
  		}
  	}
  	for(i=m;i<=n-1;i++)
  	{
  		for(j=0;j<s.size();j++)
  		{
  			if((s[j]>>(m-1))&1)//首位是 0 需要特殊处理
  			{
  				f[i+1][((s[j]^(1<<(m-1)))<<1)|1]=(f[i+1][((s[j]^(1<<(m-1)))<<1)|1]+f[i][s[j]])%p;
  			}
  			else
  			{
  				for(h=0;h<=m-1;h++)
  				{
  					if((s[j]>>h)&1)
  					{
  						f[i+1][((s[j]^(1<<h))<<1)|1]=(f[i+1][((s[j]^(1<<h))<<1)|1]+f[i][s[j]])%p;
  					}
  				}
  			}
  		}
  	}
  	for(j=0;j<s.size();j++)
  	{
  		ans=(ans+f[n][s[j]])%p;
  	}
  	cout<<ans<<endl;
  	return 0;
  }
  

$T3$ GHzoj 3733. 线段树

• 部分分

  

  

• 正解

  • 由题，有 $f_{l,r}$ 的下界至少为 $1$ ，即 $\sum _{i=1}^q{f}_{l_i,r_i}$ 最小为 $q$ 。考虑如何维护其因分割造成的其他贡献。
  • 对于线段树一段区间 $[L,R]$ 若这段区间与询问区间 $[l,r]$ 有交集但不是包含关系，那么当将其分成 $[L,k]$ 和 $[k+1,r]$ 两段区间时询问区间 $[l,r]$ 会递归进入 $[L,R]$ 的子树内继续计算贡献，从而会至少增加 $1$ 的贡献。
  • 设 $d{p}_{l,r}$ 表示对于线段树上的区间 $[l,r]$ 划分后对询问产生的其贡献的最小值，状态转移方程为 $d{p}_{l,r}=\underset{k=l}{\overset{r-1}{min}}\{d{p}_{l,k}+d{p}_{k+1,r}+val(l,r,k)\}$ ，其中 $val(l,r,k)$ 表示有多少个询问的区间和 $[l,r]$ 有交集但不是包含关系，且包含了 $k+1$ 。计算有多少个询问区间内包含 $k+1$ ，有多少个询问区间包含 $[l,r]$ ，二者相减即可。
  • 前者差分或者暴力修改即可维护，后者二维偏序或将式子拆开容斥下即可维护。
  点击查看代码

  ll a[510][510],sum[510][510],w[510],dp[510][510];
  int main()
  {
  	ll n,q,i,j,k,len,l,r;
  	cin>>n>>q;
  	for(i=1;i<=q;i++)
  	{
  		cin>>l>>r;
  		a[l][r]++;
  		for(j=l;j<=r-1;j++)
  		{
  			w[j]++;
  		}
  	}
  	for(l=1;l<=n;l++)
  	{
  		for(r=n;r>=l;r--)
  		{
  			sum[l][r]=sum[l-1][r]+sum[l][r+1]-sum[l-1][r+1]+a[l][r];
  		}
  	}
  	for(len=2;len<=n;len++)
  	{
  		for(l=1,r=l+len-1;r<=n;l++,r++) 
  		{
  			dp[l][r]=0x7f7f7f7f;
  			for(k=l;k<=r-1;k++)
  			{
  				dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]+w[k]-sum[l][r]);
  			}
  		}
  	}
  	cout<<dp[1][n]+q<<endl;
  	return 0;
  }
  

$T4$ GHzoj 3734. 公路

• 弱化版： luogu P9749 [CSP-J 2023] 公路

• 强化版： luogu P1016 [NOIP1999 提高组] 旅行家的预算 | luogu P2209 [USACO13OPEN] Fuel Economy S

• 部分分

  

  

• 正解

  • 假设当前在第 $i$ 个加油站。若在能到达的范围内存在一个最近的加油站 $j$ 使得 $a_j<a_i$ ，则只加足够到第 $j$ 个加油站的油量；否则加满油，到达能到达的范围内价格最便宜的加油站。

    点击查看代码

    ll v[100010],a[100010],sum[100010];
    int main()
    {
    	ll n,c,ans=0,num=0,pos,minn,i,j;
    	cin>>n>>c;
    	for(i=1;i<=n;i++)
    	{
    		cin>>v[i];	
    		sum[i+1]=sum[i]+v[i];
    	}
    	for(i=1;i<=n;i++)
    	{
    		cin>>a[i];
    	}
    	for(i=1;i<=n;i=j)
    	{
    		pos=0;
    		minn=0x7f7f7f7f7f7f7f7f;
    		for(j=i+1;j<=n+1&&sum[j]-sum[i]<=c;j++)
    		{
    			if(minn>a[j])
    			{
    				minn=a[j];
    				pos=j;
    			}
    			if(a[i]>a[j])
    			{
    				ans+=(sum[j]-sum[i]-num)*a[i];//num 表示已经买了多少升油
    				num=0;//因为每升油可以让车前进 1 公里，所以不涉及买整数还是小数升油（虽然题目中已经说了买整数升油）
    				break;
    			}
    		}
    		if(minn>=a[i])
    		{
    			j=pos;
    			ans+=(c-num)*a[i];
    			num=c-(sum[j]-sum[i]);
    		}
    	}
    	cout<<ans<<endl;
    	return 0;
    }
    

• 官方题解

  

  

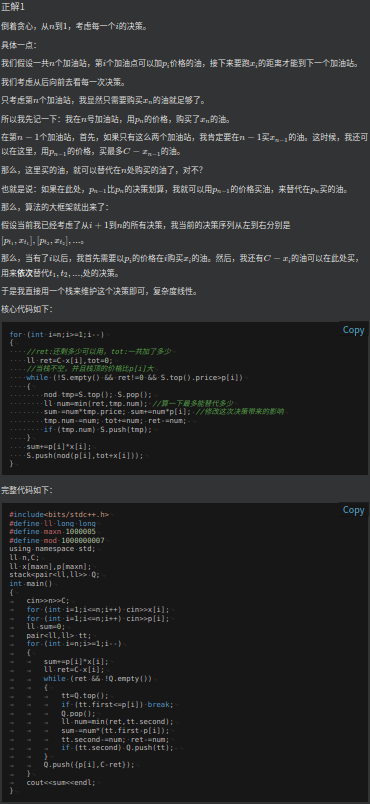
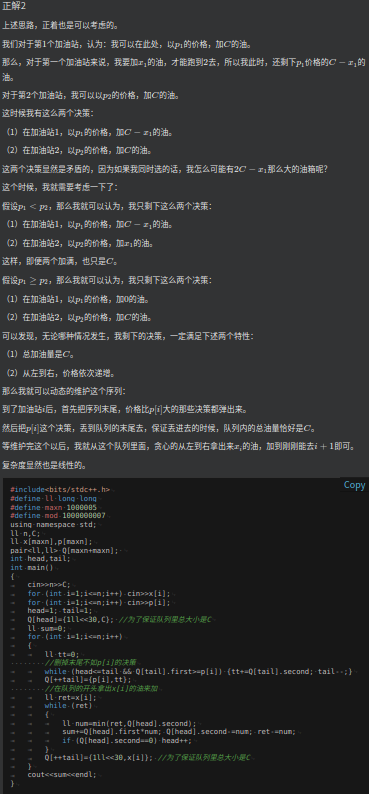
总结

• $T2$ 没有看到题面已经给出的大样例（样例 $3$ ）。
• $T3$ 读假题了，以为要找到一种合法的构造方式。
• $T4$ 把题想复杂了，没想到怎么反悔贪心。记得当时还跟 @hly_shen 论辩贪心策略呢。

后记

• 大样例直接把测试数据薅来了， $T3$ 特判样例即可骗到 $5pts$ ， $T4$ 特判样例即可骗到 $4pts$ 。