NOIP2024模拟1
1.高一上七月上旬日记2.牛客周赛 Round 493.Denso Create Programming Contest 2024(AtCoder Beginner Contest 361)
4.NOIP2024模拟1
5.NOIP2024模拟26.高一上七月中旬日记7.NOIP2024模拟38.CSP提高组模拟19.暑假集训CSP提高模拟110.暑假集训CSP提高模拟211.暑假集训CSP提高模拟312.暑假集训CSP提高模拟413.高一上七月下旬日记14.暑假集训 加赛115.暑假集训CSP提高模拟516.暑假集训CSP提高模拟617.加赛218.暑假集训CSP提高模拟719.暑假集训CSP提高模拟820.暑假集训CSP提高模拟921.暑假集训CSP提高模拟1022.暑假集训CSP提高模拟1123.暑假集训CSP提高模拟12NOIP2024模拟1

-
数据加强版: U203804 test1(只输出最多小组数)
-
设最终答案中有
-
得到不等式组
-
最终,有
点击查看代码
ll f[100010],cnt[5]; queue<ll>q[5]; int main() { ll n,ans=0,pos=0,i,j,k,a,b,c,d; cin>>n; for(i=1;i<=n;i++) { cin>>f[i]; cnt[f[i]%3]++; q[f[i]%3].push(i); } for(b=0;b<=min(cnt[0],min(cnt[1],cnt[2]));b++) { a=(cnt[1]-b)/3; c=(cnt[0]-b)/3; d=(cnt[2]-b)/3; if(a+b+c+d>ans) { ans=a+b+c+d; pos=b; } } cout<<ans<<endl; if(ans!=0) { for(i=1;i<=pos;i++) { for(k=0;k<=2;k++) { cout<<q[k].front()<<" "; q[k].pop(); } cout<<endl; } for(k=0;k<=2;k++) { for(i=1;i<=(cnt[k]-pos)/3;i++) { for(j=1;j<=3;j++) { cout<<q[k].front()<<" "; q[k].pop(); } cout<<endl; } } } return 0; }
-
部分分
-
点击查看代码
char s[100010]; int main() { ll n,k,suma=0,sumb=0,ansa=0,ansb=0,i; cin>>n>>k>>(s+1); for(i=1;i<=n;i++) { if(s[(i-1)%k+1]=='A') { suma++; if(suma>=11&&suma-sumb>=2) { ansa++; suma=sumb=0; } } else { sumb++; if(sumb>=11&&sumb-suma>=2) { ansb++; suma=sumb=0; } } } cout<<ansa<<":"<<ansb<<endl; return 0; }
-
-
正解
- 猜测在一定条件下,
zwh和小红的得分是会有循环节的。而这个条件主要限制来自 - 预先排除无意义追分,比如
ABAB或BABA。 - 若在新的一轮环节开始时,
zwh和小红已经进入追分环节,二人分数同时减少一个定值使其缩小至 - 设
zwh和小红的单局比赛比分为zwh和小红分别胜了zwh和小红的单局比赛比分为zwh和小红分别胜了zwh和小红分别增加的胜的场数为
点击查看代码
ll len[100010],to[100010],va[100010],vb[100010]; char s[100010]; void ask(ll pos,ll newlen,ll newa,ll newb,ll &ansa,ll &ansb,ll n) { if(len[pos]<=n) { ansa+=va[pos]+(n-len[pos])/(newlen-len[pos])*(newa-va[pos]);//计算循环节的贡献 ansb+=vb[pos]+(n-len[pos])/(newlen-len[pos])*(newb-vb[pos]); n=(n-len[pos])%(newlen-len[pos]);//除去多出来的部分 } else { pos=0; } ll st=pos; while(len[to[pos]]-len[st]<=n&&to[pos]!=st) { pos=to[pos]; } ansa+=va[pos]-va[st];//计算多出来的贡献 ansb+=vb[pos]-vb[st]; } int main() { ll n,k,suma,sumb,ansa=0,ansb=0,flag=0,i,j,pos; cin>>n>>k>>(s+1); s[0]=s[k]; memset(to,0x3f,sizeof(to)); for(i=0;i<=k;) { pos=i; suma=sumb=0; for(j=1;;j++)//开始找循环节,记录步数 { if(j>=max(k,22ll)*2+2)//无意义追分 { flag=1; break; } i=(i+1)%k; suma+=(s[i]=='A'); sumb+=(s[i]=='B'); if(suma>=11&&suma-sumb>=2) { to[pos]=i; if(to[i]<k)//第二次遇到,找到循环节了 { ask(i,len[pos]+j,va[pos]+1,vb[pos],ansa,ansb,n); flag=1; } len[i]=len[pos]+j; va[i]=va[pos]+1; vb[i]=vb[pos]; break; } if(sumb>=11&&sumb-suma>=2) { to[pos]=i; if(to[i]<k)//第二次遇到,找到循环节了 { ask(i,len[pos]+j,va[pos],vb[pos]+1,ansa,ansb,n); flag=1; } len[i]=len[pos]+j; va[i]=va[pos]; vb[i]=vb[pos]+1; break; } } if(flag==1) { break; } } cout<<ansa<<":"<<ansb<<endl; return 0; } - 猜测在一定条件下,
-
部分分

-
正解
- 容易有
|...|&...&|...|,其中&...&中可能会夹杂着|。 - 展开后按位前缀和统计
点击查看代码
ll a[200010],sum[200010][70]; char s[200010]; ll ask(ll l,ll k,ll n,ll num) { if(l<=n-k)//[l,n-k] 是 & { for(ll i=0;i<=60;i++) { if(((num>>i)&1)&&sum[n-k][i]-sum[l-1][i]!=n-k-l+1) { num-=(1ll<<i); } } } if(n-k+1<=n)//(n-k,n] 是 | { for(ll i=0;i<=60;i++) { if(sum[n][i]-sum[n-k+1-1][i]!=0) { num|=(1ll<<i); } } } return num; } int main() { ll n,k,ans,num,i,j; cin>>n>>k; for(i=1;i<=n;i++) { cin>>a[i]; for(j=0;j<=60;j++) { sum[i][j]=sum[i-1][j]+((a[i]>>j)&1); } } ans=ask(2,k,n,a[1]); cout<<ans<<endl; num=a[1]; for(i=2;i<=n;i++) { if(k>=1&&ask(i+1,k-1,n,num|a[i])==ans) { num|=a[i]; k--; cout<<"|"; } else { num&=a[i]; cout<<"&"; } } return 0; } - 容易有
-
- 令
-
设
-
边界如果处理得不恰当,则会被
点击查看 hack 数据 1
in: 5 3 8 9 20 18 ans: 4点击查看 hack 数据 2
in: 3 342982640 708917468 453005496 ans: 2
-
-
设
-
最终,有
- 其实
点击查看代码
ll a[510],d[510][510],f[510][510],dp[510]; ll gcd(ll a,ll b) { return b?gcd(b,a%b):a; } int main() { ll n,i,j,k,len,l,r; cin>>n; a[0]=1; for(i=1;i<=n;i++) { cin>>a[i]; } a[n+1]=1; for(i=1;i<=n;i++) { for(j=1;j<=n;j++) { d[i][j]=gcd(a[i],a[j]); } } for(i=1;i<=n+1;i++) { for(j=0;j<=i-1;j++) { f[i][j]=1; } if(d[i][i-1]>1||d[i][i+1]>1) { f[i][i]=1; } } for(len=2;len<=n;len++) { for(l=1,r=l+len-1;r<=n;l++,r++) { for(k=l;k<=r;k++) { f[l][r]=max(f[l][r],f[l][k-1]*f[k+1][r]*(d[k][l-1]>1||d[k][r+1]>1)); } } } dp[0]=dp[1]=0; for(i=2;i<=n+1;i++) { for(j=0;j<=i-1;j++) { dp[i]=max(dp[i],dp[j]+f[j+1][i-1]*((i-1)-(j+1)+1)); } } cout<<dp[n+1]<<endl; return 0; } - 其实
-
-
部分分
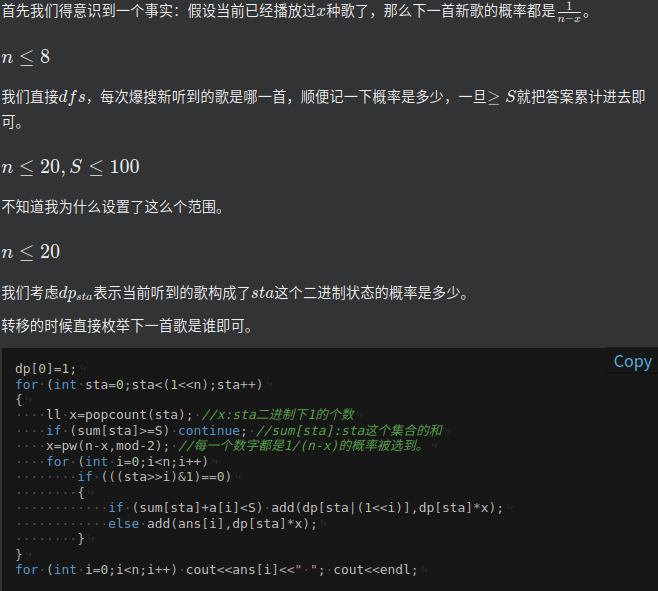
-
正解
- 设
- 对于每个
- 枚举
点击查看代码
const ll p=998244353; ll a[110],inv[110],jc[110],jc_inv[110],f[110][10010]; ll A(ll n,ll m,ll p) { return (n>=m&&n>=0&&m>=0)?jc[n]*jc_inv[n-m]%p:0; } ll A_inv(ll n,ll m,ll p) { return (n>=m&&n>=0&&m>=0)?jc_inv[n]*jc[n-m]%p:0; } int main() { ll n,s,ans=0,i,j,k; cin>>n>>s; for(i=1;i<=n;i++) { cin>>a[i]; } inv[1]=1; jc[0]=jc_inv[0]=jc[1]=jc_inv[1]=1; for(i=2;i<=n;i++) { inv[i]=(p-p/i)*inv[p%i]%p; jc[i]=jc[i-1]*i%p; jc_inv[i]=jc_inv[i-1]*inv[i]%p; } f[0][0]=1; for(i=1;i<=n;i++) { for(j=n-1;j>=0;j--) { for(k=0;k<=s-a[i]-1;k++) { f[j+1][k+a[i]]=(f[j+1][k+a[i]]+f[j][k])%p; } } } for(i=1;i<=n;i++) { ans=0; for(j=0;j<=n-1;j++) { for(k=0;k<=s-a[i]-1;k++) { f[j+1][k+a[i]]=(f[j+1][k+a[i]]-f[j][k]+p)%p; } } for(j=0;j<=n-1;j++) { for(k=s-a[i];k<=s-1;k++) { ans=(ans+(f[j][k]*A(j,j,p)%p)*A_inv(n,j+1,p)%p)%p; } } for(j=n-1;j>=0;j--) { for(k=0;k<=s-a[i]-1;k++) { f[j+1][k+a[i]]=(f[j+1][k+a[i]]+f[j][k])%p; } } cout<<ans<<" "; } return 0; } - 设
-
总结
- 有大样例,赢。
admin外最劣解。一开始少了一种情况下发大样例后调了半天才发现,还特意写了个阉割般的Special Judge来检验答案,力挽狂澜,要不然就没 @STA_Morlin 分高了。1<<i最终的类型是int,但1ll<<i最终的类型是long long调了半天。- 以前在 挂分记(持续更新ing...) luogu月赛 10.2 基础赛 见过这个,但没想起来。
后记
-
信息与公告如下。要是明年

-
题目背景多次出现
-
Special Judge,导致交的早的没有Special Judge,交的晚的才有Special Judge。赛后安排了重测。 -
数据太水了,放掉了不少的假贪心和边界处理不恰当的代码。
-
官方题解中防抄袭代码明显。
本文来自博客园,作者:hzoi_Shadow,原文链接:https://www.cnblogs.com/The-Shadow-Dragon/p/18290590,未经允许严禁转载。
版权声明:本作品采用 「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0) 进行许可。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】