九下五月中旬日记
5.11
闲话
- 详见 2024 HE中考 游记 5.11 。
- \(13:10\) 左右突然腿抽筋了,叫了出来,不知道当时有没有被宿管听见。
- 从宿舍到机房的路上在晒草,占了整个小操场和多半部分的路。
- 下午大课间问了下 @_君の名は 他们接下来要学啥。
- 高一的体活貌似可以拿到 【数据删除】 ,上届初三的体活貌似也可以动老师电脑,怎么这届初三没有这等福气。
- 体活因为 \(miaomiao\) 不在,所以不知道现班主任有没有来找我们。然后找 \(field\) 批 ABC 的假(整个晚上),但是 \(field\) 不认识现班主任,现班主任也不认识 \(field\) ,关键最后还真批下来了。
- 吃完晚饭回来, @_君の名は 来找我们唠嗑。
- 晚上貌似是文综周测,班里信奥占了两列,最后两个是生奥的,一个请假回家了,也就是说两列只有一个人在班里,体验到了孤独的感觉。
做题纪要
luogu P2486 [SDOI2011] 染色
-
线段树维护左右端点颜色即可。
-
查询时在跳重链的过程中减去路径交汇处的贡献,故在同一条重链上时就不需要再进行统计。
点击查看代码
struct node { int nxt,to; }e[200010]; int head[200010],c[200010],cc[200010],siz[200010],fa[200010],dep[200010],son[200010],top[200010],dfn[200010],cnt=0,tot=0; struct SegmentTree { int l,r,lazy,lc,rc,ans; }tree[800010]; int lson(int x) { return x*2; } int rson(int x) { return x*2+1; } void pushup(int rt) { tree[rt].ans=tree[lson(rt)].ans+tree[rson(rt)].ans-(tree[lson(rt)].rc==tree[rson(rt)].lc); tree[rt].lc=tree[lson(rt)].lc; tree[rt].rc=tree[rson(rt)].rc; } void build(int rt,int l,int r) { tree[rt].l=l; tree[rt].r=r; if(l==r) { tree[rt].lc=tree[rt].rc=cc[l]; tree[rt].ans=1; tree[rt].lazy=0; return; } int mid=(l+r)/2; build(lson(rt),l,mid); build(rson(rt),mid+1,r); pushup(rt); } void pushdown(int rt) { if(tree[rt].lazy!=0) { tree[lson(rt)].lc=tree[lson(rt)].rc=tree[rt].lazy; tree[rson(rt)].lc=tree[rson(rt)].rc=tree[rt].lazy; tree[lson(rt)].ans=1; tree[rson(rt)].ans=1; tree[lson(rt)].lazy=tree[rt].lazy; tree[rson(rt)].lazy=tree[rt].lazy; tree[rt].lazy=0; } } void update(int rt,int x,int y,int val) { if(x<=tree[rt].l&&tree[rt].r<=y) { tree[rt].lc=tree[rt].rc=val; tree[rt].ans=1; tree[rt].lazy=val; return; } pushdown(rt); int mid=(tree[rt].l+tree[rt].r)/2; if(x<=mid) { update(lson(rt),x,y,val); } if(y>mid) { update(rson(rt),x,y,val); } pushup(rt); } SegmentTree query(int rt,int x,int y) { if(x<=tree[rt].l&&tree[rt].r<=y) { return tree[rt]; } pushdown(rt); int mid=(tree[rt].l+tree[rt].r)/2; SegmentTree ans,num; ans.ans=ans.lc=ans.rc=0; if(x<=mid) { num=query(lson(rt),x,y); ans.ans+=num.ans; ans.lc=num.lc; ans.rc=num.rc; } if(y>mid) { num=query(rson(rt),x,y); if(ans.lc==0) { ans.ans+=num.ans; ans.lc=num.lc; ans.rc=num.rc; } else { ans.ans+=num.ans-(ans.rc==num.lc); ans.rc=num.rc; } } return ans; } void add(int u,int v) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt; } void dfs1(int x,int father) { siz[x]=1; fa[x]=father; dep[x]=dep[father]+1; for(int i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=father) { dfs1(e[i].to,x); siz[x]+=siz[e[i].to]; son[x]=(siz[e[i].to]>siz[son[x]])?e[i].to:son[x]; } } } void dfs2(int x,int father,int id) { top[x]=id; tot++; dfn[x]=tot; cc[tot]=c[x]; if(son[x]!=0) { dfs2(son[x],x,id); for(int i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=father&&e[i].to!=son[x]) { dfs2(e[i].to,x,e[i].to); } } } } void update1(int u,int v,int val) { while(top[u]!=top[v]) { if(dep[top[u]]>dep[top[v]]) { update(1,dfn[top[u]],dfn[u],val); u=fa[top[u]]; } else { update(1,dfn[top[v]],dfn[v],val); v=fa[top[v]]; } } if(dep[u]<dep[v]) { update(1,dfn[u],dfn[v],val); } else { update(1,dfn[v],dfn[u],val); } } int query1(int u,int v) { int ans=0; while(top[u]!=top[v]) { if(dep[top[u]]>dep[top[v]]) { ans+=query(1,dfn[top[u]],dfn[u]).ans-(query(1,dfn[top[u]],dfn[top[u]]).lc==query(1,dfn[fa[top[u]]],dfn[fa[top[u]]]).lc); u=fa[top[u]]; } else { ans+=query(1,dfn[top[v]],dfn[v]).ans-(query(1,dfn[top[v]],dfn[top[v]]).lc==query(1,dfn[fa[top[v]]],dfn[fa[top[v]]]).lc); v=fa[top[v]]; } } if(dep[u]<dep[v]) { ans+=query(1,dfn[u],dfn[v]).ans; } else { ans+=query(1,dfn[v],dfn[u]).ans; } return ans; } int main() { int n,m,u,v,w,i; char pd; cin>>n>>m; for(i=1;i<=n;i++) { cin>>c[i]; } for(i=1;i<=n-1;i++) { cin>>u>>v; add(u,v); add(v,u); } dfs1(1,0); dfs2(1,0,1); build(1,1,n); for(i=1;i<=m;i++) { cin>>pd>>u>>v; if(pd=='C') { cin>>w; update1(u,v,w); } else { cout<<query1(u,v)<<endl; } } return 0; }
luogu P2605 [ZJOI2010] 基站选址
-
考虑在末尾插入一个村庄 \(n+1\) ,满足 \(\begin{cases} d_{n+1}=\infty \\ c_{n+1}=0 \\ s_{n+1}=0 \\ w_{n+1}=0 \end{cases}\) 。且强制在 \(n+1\) 建立通讯基站,这样的话需要多一个通讯基站。
-
设 \(f_{i,j}\) 表示前 \(i\) 个村庄建了 \(j\) 个通讯基站,且第 \(i\) 个村庄建立通讯基站的最小总费用,状态转移方程为 \(\begin{cases} f_{i,j}=c_{i}+\sum\limits_{l=1}^{i-1}[d_{l}+s_{l}<d_{i}] \times w_{l} & j=1 \\ f_{i,j}=c_{i}+\min\limits_{h=j-1}^{i-1} \{ f_{h,j-1}+\sum\limits_{l=h+1}^{i-1}[d_{h}<d_{l}-s_{l}] \times [d_{l}+s_{l}<d_{i}] \times w_{l} \} & 2 \le j \le \min(i,k) \end{cases}\) 。
-
考虑二分出第 \(i\) 个村庄所能覆盖的最长区间 \([L_{i},R_{i}]\) 和第 \(i\) 个村庄作为哪些村庄所能覆盖的最长区间的右端点,状态转移方程改写为 \(\begin{cases} f_{i,j}=c_{i}+\sum\limits_{l=1}^{i-1}[d_{l}+s_{l}<d_{i}] \times w_{l} & j=1 \\ f_{i,j}=c_{i}+\min\limits_{h=j-1}^{i-1} \{ f_{h,j-1}+\sum\limits_{l=R_{h}+1}^{L_{i}-1}w_{l} \} & 2 \le j \le \min(i,k) \end{cases}\) 。
-
考虑对 \(f_{h,j-1}+\sum\limits_{l=R_{h}+1}^{L_{i}-1}w_{l}\) 建立线段树。从 \(f_{x,j-1}\) 扩展到 \(f_{x,j}\) 的过程中,先更新 \(f_{x,j}\) ,再更新 \(\sum\limits_{l=R_{h}+1}^{L_{i}-1}w_{l}\) 。
-
最终,有 \(\min\limits_{i=1}^{k+1} \{ f_{n,i} \}\) 即为所求。
点击查看代码
int f[110][20010],d[20010],c[20010],s[20010],w[20010],sum[20010],L[20010],R[20010]; vector<int>pos[20010]; struct SegmentTree { int l,r,minn,lazy; }tree[80010]; int lson(int x) { return x*2; } int rson(int x) { return x*2+1; } void pushup(int rt) { tree[rt].minn=min(tree[lson(rt)].minn,tree[rson(rt)].minn); } void build(int rt,int l,int r,int f[]) { tree[rt].l=l; tree[rt].r=r; tree[rt].lazy=0; if(l==r) { tree[rt].minn=f[l]; return; } int mid=(l+r)/2; build(lson(rt),l,mid,f); build(rson(rt),mid+1,r,f); pushup(rt); } void pushdown(int rt) { if(tree[rt].lazy!=0) { tree[lson(rt)].minn+=tree[rt].lazy; tree[rson(rt)].minn+=tree[rt].lazy; tree[lson(rt)].lazy+=tree[rt].lazy; tree[rson(rt)].lazy+=tree[rt].lazy; tree[rt].lazy=0; } } void update(int rt,int x,int y,int val) { if(x<=tree[rt].l&&tree[rt].r<=y) { tree[rt].minn+=val; tree[rt].lazy+=val; return; } pushdown(rt); int mid=(tree[rt].l+tree[rt].r)/2; if(x<=mid) { update(lson(rt),x,y,val); } if(y>mid) { update(rson(rt),x,y,val); } pushup(rt); } int query(int rt,int x,int y) { if(x<=tree[rt].l&&tree[rt].r<=y) { return tree[rt].minn; } pushdown(rt); int mid=(tree[rt].l+tree[rt].r)/2,ans=0x7f7f7f7f; if(x<=mid) { ans=min(ans,query(lson(rt),x,y)); } if(y>mid) { ans=min(ans,query(rson(rt),x,y)); } return ans; } int main() { int n,k,ans=0x7f7f7f7f,i,j,h; cin>>n>>k; for(i=2;i<=n;i++) { cin>>d[i]; } for(i=1;i<=n;i++) { cin>>c[i]; } for(i=1;i<=n;i++) { cin>>s[i]; } for(i=1;i<=n;i++) { cin>>w[i]; sum[i]=sum[i-1]+w[i]; } n++; d[n]=0x7f7f7f7f; c[n]=s[n]=w[n]=0; sum[n]=sum[n-1]+w[n]; k++; for(i=1;i<=n;i++) { L[i]=lower_bound(d+1,d+1+n,d[i]-s[i])-d; R[i]=upper_bound(d+1,d+1+n,d[i]+s[i])-d-1; pos[R[i]].push_back(i); } for(i=1;i<=1;i++) { for(j=1;j<=n;j++) { f[1][j]=c[j]; for(h=1;h<=j-1;h++) { f[1][j]+=(s[h]+d[h]<d[j])*w[h]; } } ans=min(ans,f[i][n]); } for(i=2;i<=k;i++) { build(1,1,n,f[i-1]); for(j=1;j<=n;j++) { f[i][j]=c[j]+((j-1>=i-1)?query(1,i-1,j-1):0); for(h=0;h<pos[j].size();h++) { if(L[pos[j][h]]-1>=1)//更新影响 { update(1,1,L[pos[j][h]]-1,w[pos[j][h]]); } } } ans=min(ans,f[i][n]); } cout<<ans<<endl; return 0; }
[ABC353A] Buildings
-
模拟即可。
点击查看代码
int h[120]; int main() { int n,ans=-1,i; cin>>n; for(i=1;i<=n;i++) { cin>>h[i]; if(i>=2&&h[i]>h[1]) { ans=i; break; } } cout<<ans<<endl; return 0; }
[ABC353E] Yet Another Sigma Problem
-
将所有字符串拼起来,并得到相应的 \(a_{i}\) ,在 1.字符串专题 B CF1073G Yet Another LCP Problem 中已经介绍了如何求 \(\sum\limits_{i=1}^{k}\sum\limits_{j=i+1}^{k}LCP(s_{a_{i} \sim n},s_{a_{j} \sim n})\) ,这里不再赘述。
点击查看代码
ll s[600010],sa[600010],rk[1600010],oldrk[1600010],id[600010],cnt[600010],key[600010],height[600010],a[600010],b[600010],c[600010],fminn[600010][20],f[600010],g[600010]; char t[600010]; bool cmp(ll a,ll b) { return rk[a]<rk[b]; } ll val(char x) { return (ll)x; } void counting_sort(ll n,ll m) { memset(cnt,0,sizeof(cnt)); for(ll i=1;i<=n;i++) { cnt[key[i]]++; } for(ll i=1;i<=m;i++) { cnt[i]+=cnt[i-1]; } for(ll i=n;i>=1;i--) { sa[cnt[key[i]]]=id[i]; cnt[key[i]]--; } } void init_sa(ll s[],ll len) { ll m=600010,tot=0,num=0,i,j,w; for(i=1;i<=len;i++) { rk[i]=s[i]; id[i]=i; key[i]=rk[id[i]]; } counting_sort(len,m); for(w=1;tot!=len;w<<=1,m=tot) { num=0; for(i=len;i>=len-w+1;i--) { num++; id[num]=i; } for(i=1;i<=len;i++) { if(sa[i]>w) { num++; id[num]=sa[i]-w; } } for(i=1;i<=len;i++) { key[i]=rk[id[i]]; } counting_sort(len,m); for(i=1;i<=len;i++) { oldrk[i]=rk[i]; } tot=0; for(i=1;i<=len;i++) { tot+=(oldrk[sa[i]]!=oldrk[sa[i-1]]||oldrk[sa[i]+w]!=oldrk[sa[i-1]+w]); rk[sa[i]]=tot; } } for(i=1,j=0;i<=len;i++) { j-=(j>=1); while(s[i+j]==s[sa[rk[i]-1]+j]) { j++; } height[rk[i]]=j; } } void init(ll n,ll a[]) { memset(fminn,0x3f,sizeof(fminn)); for(ll i=1;i<=n;i++) { fminn[i][0]=a[i]; } for(ll j=1;j<=log2(n);j++) { for(ll i=1;i<=n-(1<<j)+1;i++) { fminn[i][j]=min(fminn[i][j-1],fminn[i+(1<<(j-1))][j-1]); } } } ll query(ll l,ll r) { ll t=log2(r-l+1); return min(fminn[l][t],fminn[r-(1<<t)+1][t]); } ll ask(ll n,ll a[]) { ll sum=0,i; stack<ll>st; sort(a+1,a+1+n,cmp); for(i=1;i<=n;i++) { g[i]=((a[i]==a[i-1])?n-a[i]+1:query(rk[a[i-1]]+1,rk[a[i]])); } for(i=1;i<=n;i++) { while(st.empty()==0&&g[st.top()]>=g[i]) { st.pop(); } if(st.empty()==0) { f[i]=f[st.top()]+g[i]*(i-st.top()); } else { f[i]=f[0]+g[i]*(i-0); } st.push(i); sum+=f[i]; } return sum; } int main() { ll n,len=0,lent,mm=0,i,j; cin>>n; for(i=1;i<=n;i++) { scanf("%s",t+1); lent=strlen(t+1); a[i]=len+1; for(j=1;j<=lent;j++) { len++; s[len]=val(t[j]); } len++; mm++; s[len]='z'+mm; } init_sa(s,len); init(len,height); cout<<ask(n,a)<<endl; return 0; }
[ABC353B] AtCoder Amusement Park
-
顺序结构。
点击查看代码
int a[110]; int main() { int n,k,ans=0,sum=0,i; cin>>n>>k; for(i=1;i<=n;i++) { cin>>a[i]; if(sum==0) { sum=a[i]; ans++; } else { if(k-sum<a[i]) { sum=a[i]; ans++; } else { sum+=a[i]; } } } cout<<ans<<endl; return 0; }
[ABC353C] Sigma Problem
-
发现对 \(1 \times 10^{8}\) 取模在 \(\sum\) 里面很难处理,考虑将其分组,分成 \(<5 \times 10^{7}\) 和 \(\ge 5 \times 10^{7}\) 两组。
- 不分组也行,只是比较难处理。
-
观察到 \(a_{i} \le 1 \times 10^{8}\) ,故在第二组内可以把对 \(1 \times 10^{8}\) 取模写成减 \(1 \times 10^{8}\) ,又因为是两个数相加,故可以各减去 \(5 \times 10^{7}\) 。
点击查看代码
const ll p=100000000; ll a[300010],b[300010],c[300010],sum[300010]; int main() { ll n,n1=0,n2=0,ans=0,pos,i; cin>>n; for(i=1;i<=n;i++) { cin>>a[i]; if(a[i]<50000000) { n1++; b[n1]=a[i]; sum[n1]=sum[n1-1]+b[n1]; } else { n2++; c[n2]=a[i]; } } sort(b+1,b+1+n1); sort(c+1,c+1+n2); for(i=1;i<=n1;i++) { ans+=b[i]*(n1-1); } for(i=1;i<=n2;i++) { ans+=(c[i]-50000000)*(n2-1); pos=lower_bound(b+1,b+1+n1,p-c[i])-b; if(pos>n1) { ans+=c[i]*n1+sum[n1]; } else { ans+=c[i]*n1+sum[n1]-p*(n1-pos+1); } } cout<<ans<<endl; return 0; }
5.12
闲话
- 英语周测,现英语老师收二卷只拿到了一部分,“这数量也不够了,一摸也就才三十多张”,正准备发飙了,突然看见前面桌子上还有一沓,拿起来走了。
- 数学周测
- \(22\) 题没告诉我甲、乙两个茶叶厂各有多少个茶叶,我怎么知道怎么算。
- \(25(3)\) 让求满足 \(y=4x+16\) 和 \(y=\frac{1}{4}(x-t)^{2}+4t-4(t>0,t \ne 2)\) 的交点的纵坐标 \(\le t^{2}\) 的 \(t\) 的最大值。口胡了一个数形结合做法,取了 \(\begin{cases} y_{1}=4x+16 \\ y_{2}=\frac{1}{4}(x-t)^{2}+4t-4 \\ y_{3}=t^{2} \end{cases}\) 过同一点的做法,以为自己做错了,但发下答案后自己写对了。
- \(25(3)\) 只有 \(2pts\) ,计算量却很大。
- \(26(3)\) 只有 \(4pts\) ,计算量却很大。
- 理综周测
- 上周现化学老师记错卷头了,有道题被提前透题了,虽说其也很水。
- 语文周测
- 因拍摄角度问题,无法分析出是什么字体,仅能通过选项判断正误。
- 综合性学习之一是课本剧,让我们模拟导演,以前同宿舍的一个人瑞平“让我当导演啊,我可得好好导一发啊”。
- 实际上是九下的一个课后活动,讲评时强调“课本在手”。
- 作文主题是双向奔赴。讲评时强调“不能写自己与自己、自己与梦想”,“必须写人与人”,“最好不要写爱情”。
- 晚上发现现班主任又双叒叕出差了,所以没开班会,一整节课十分漫长。
做题纪要
5.13
闲话
- 物理课上现物理老师提醒我们要收收心,现在各科作业和积累本都懒得写,“回了原班可就是物是人非了,万一谁都考不过了”,还 \(D\) 了下 @HANGRY_sol 。同时得知了不到早上 \(8:00\) ,学校不给空调供电。
- 下午到机房后发现隔壁 \(2\) 机房有每日一歌,但 \(4\) 机房没有。
- \(ftp\) 机房给设成了禁止连接,前几天还是一直连不上呢。
- \(huge\) 去盯高一的去了, \(feifei\) 来盯我们。
- 下午大课间的时候 \(huge\) 对 \(feifei\) 说让我们出去活动 \(15min\) ,但初三下午大课间只有 \(10min\) , \(feifei\) 对我们仍坐在机房里面感到很困惑,问我们留在机房干啥。
- 代班主任对我们各项的到位极不满意,称让我们好好备考。
做题纪要
CF13E Holes
-
预处理出 \(last_{i}\) 表示 \(i\) 跳出 \(i\) 所在块前所处的最后一个位置 ,状态转移方程为 \(last_{i}=\begin{cases} i & i+a_{i} \ge R_{pos_{i}} \\ last_{i+a_{i}} & i+a_{i}<R_{pos_{i}} \end{cases}\) 。
点击查看代码
int a[100010],L[100010],R[100010],pos[100010],sum[100010],to[100010],last[100010],klen,ksum; void init(int n) { klen=sqrt(n); ksum=n/klen; for(int i=1;i<=ksum;i++) { L[i]=R[i-1]+1; R[i]=R[i-1]+klen; } if(R[ksum]<n) { ksum++; L[ksum]=R[ksum-1]+1; R[ksum]=n; } for(int i=1;i<=ksum;i++) { for(int j=L[i];j<=R[i];j++) { pos[j]=i; } } for(int i=ksum;i>=1;i--) { for(int j=R[i];j>=L[i];j--) { to[j]=(j+a[j]>R[i])?j+a[j]:to[j+a[j]]; sum[j]=(j+a[j]>R[i])?1:sum[j+a[j]]+1; last[j]=(j+a[j]>R[i])?j:last[j+a[j]]; } } } void update(int l,int val) { a[l]=val; for(int i=R[pos[l]];i>=L[pos[l]];i--) { to[i]=(i+a[i]>R[pos[l]])?i+a[i]:to[i+a[i]]; sum[i]=(i+a[i]>R[pos[l]])?1:sum[i+a[i]]+1; last[i]=(i+a[i]>R[pos[l]])?i:last[i+a[i]]; } } pair<int,int> query(int l,int r) { pair<int,int>ans=make_pair(0,0); for(int i=l;i<=r;i=to[i]) { ans.first=last[i]; ans.second+=sum[i]; } return ans; } int main() { int n,m,pd,l,val,i; pair<int,int>ans; scanf("%d%d",&n,&m); for(i=1;i<=n;i++) { scanf("%d",&a[i]); } init(n); for(i=1;i<=m;i++) { scanf("%d%d",&pd,&l); if(pd==1) { ans=query(l,n); printf("%d %d\n",ans.first,ans.second); } else { scanf("%d",&val); update(l,val); } } return 0; }
luogu P1525 [NOIP2010 提高组] 关押罪犯
-
考虑二分答案,将任意两个仇恨程度大于所二分的的答案之间连边,得到一张无向图。然后问题就转化成了判断这张无向图是否是二分图。
- 二分图判定板子。
- 如果一张图能把所有的点分成两个集合,保证两个集合内部没有任何边,图中的边只存在于两个集合之间,这张图就称作二分图。
- 二分图判定定理:一张无向图是二分图,当且仅当图中不存在奇环。
- 证明:每一条边都是从一个集合走向另一个集合,只有走偶数次才可能回到同一个集合。
- 用染色法进行二分图的判定。
- 用黑白两种颜色标记图中的节点,当一个节点被标记后,将它的所有相邻节点标记为于它相反的颜色。若标记的过程中产生冲突,则说明图中存在奇环。
点击查看代码
struct node { int nxt,to,w; }e[200010]; int head[200010],vis[200010],cnt=0; void add(int u,int v,int w) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; e[cnt].w=w; head[u]=cnt; } bool dfs(int x,int col,int mid) { vis[x]=col; for(int i=head[x];i!=0;i=e[i].nxt) { if(e[i].w>mid) { if(vis[e[i].to]==0) { if(dfs(e[i].to,3-col,mid)==false) { return false; } } if(vis[e[i].to]==col) { return false; } } } return true; } bool check(int mid,int n) { memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) { if(vis[i]==0&&dfs(i,1,mid)==false) { return false; } } return true; } int main() { int n,m,u,v,w,l=0,r=0,ans=0,mid,i; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v>>w; r=max(r,w); add(u,v,w); add(v,u,w); } while(l<=r) { mid=(l+r)/2; if(check(mid,n)==true) { ans=mid; r=mid-1; } else { l=mid+1; } } cout<<ans<<endl; return 0; } - 二分图判定板子。
[ABC353D] Another Sigma Problem
-
由 \(f(x,y)=x \times 10^{\left\lfloor \log_{10}y \right\rfloor+1}+y\) ,前缀和维护即可。
点击查看代码
const ll p=998244353; ll a[200010],sum[200010]; ll qpow(ll a,ll b,ll p) { ll ans=1; while(b>0) { if(b&1) { ans=ans*a%p; } b>>=1; a=a*a%p; } return ans; } int main() { ll n,ans=0,i; cin>>n; for(i=1;i<=n;i++) { cin>>a[i]; sum[i]=(sum[i-1]+a[i])%p; ans=((ans+qpow(10,log10(a[i])+1,p)*sum[i-1]%p+a[i]*(i-1)%p)%p)%p; } cout<<ans<<endl; return 0; }
luogu P3386 【模板】二分图最大匹配
-
二分图最大匹配板子。
- 定义
- 任意两条边都没有公共端点的边的集合 \(S\) 被称为图的一组匹配。
- 对于任意一组匹配 \(S\) ,属于 \(S\) 的边被称作匹配边,其他边被称作非匹配边;匹配边的端点被称作匹配点,其他点被称作非匹配点。
- 交错路:起点是非匹配点,且由匹配边与非匹配边交错组成。
- 增广路:起点和终点都是非匹配点的交错路。
- 增广路性质
- 长度 \(len\) 是奇数。
- 路径上第 \(1,3,5,\dots,len\) 条边是非匹配边,第 \(2,4,6,\dots,len-1\) 条边是匹配边。
- 增广路性质
- 增光路上非匹配边数量比匹配边数量多一,将匹配状态取反后,匹配大小会增加一且依然是交错路,称此过程为增广。
- 在二分图中,包含边数最多的一组匹配被称为二分图的最大匹配。
- 增广路定理
- 二分图的一组匹配 \(S\) 是最大匹配当且仅当图中不存在 \(S\) 的增广路。
- 匈牙利算法(增广路算法)
- 找到一条增广路后把路径上所有边的匹配状态取反,得到更大的匹配,直至图中不存在增广路。
- 现在问题转化成了如何找到一条增广路。
- 尝试给每一个左部节点 \(x\) 找到一个右部节点 \(y\) 与之匹配,必须满足以下两个条件之一:
- \(y\) 是非匹配点。
- 此时可以得到一条长度为 \(1\) 的增广路 \(path= \{ (x,y) \}\) 。
- \(y\) 已经与左部节点 \(x'\) 匹配,但从 \(x'\) 出发能找到另一个右部节点 \(y'\) 与之匹配。
- 此时可以得到的增广路 \(path= \{ (x,y),(x',y') \}\) 。
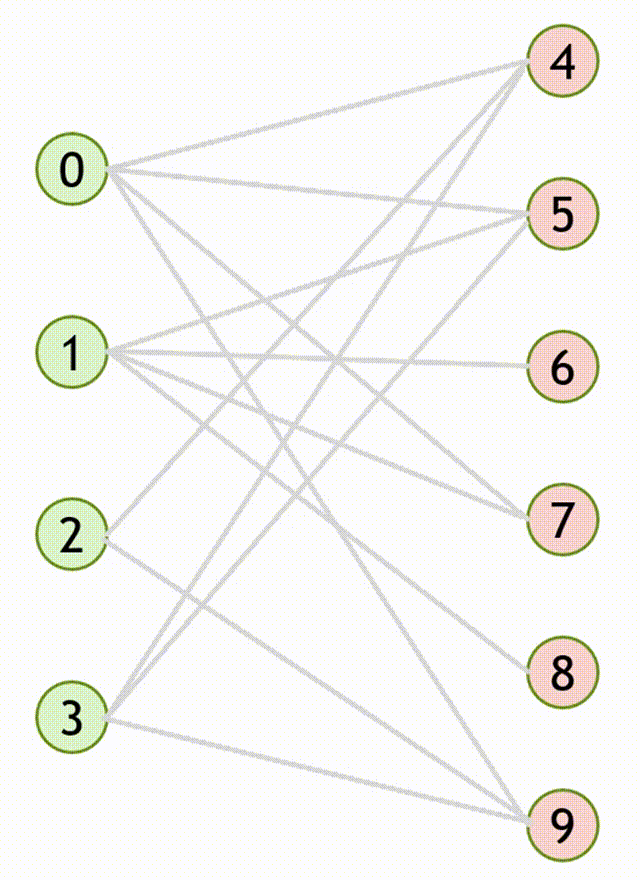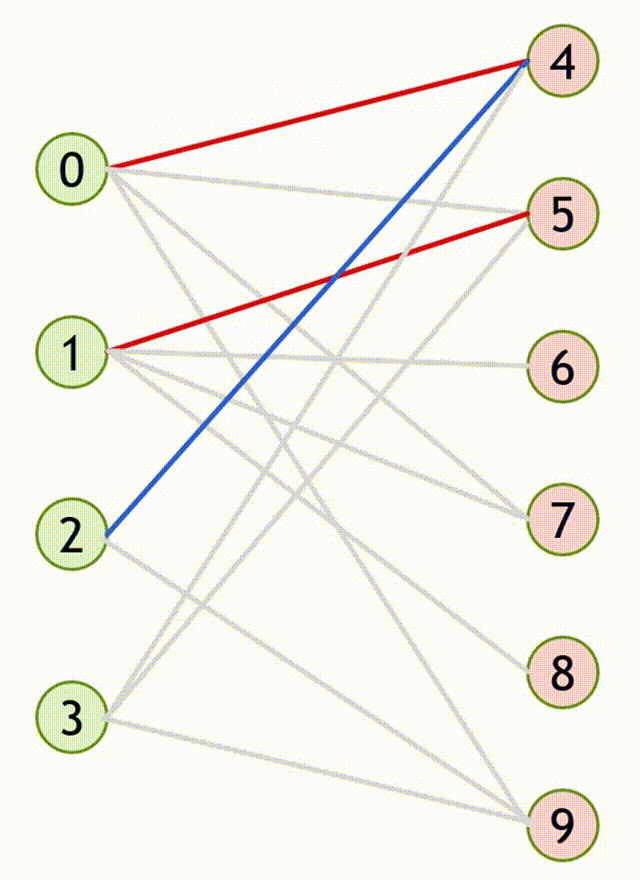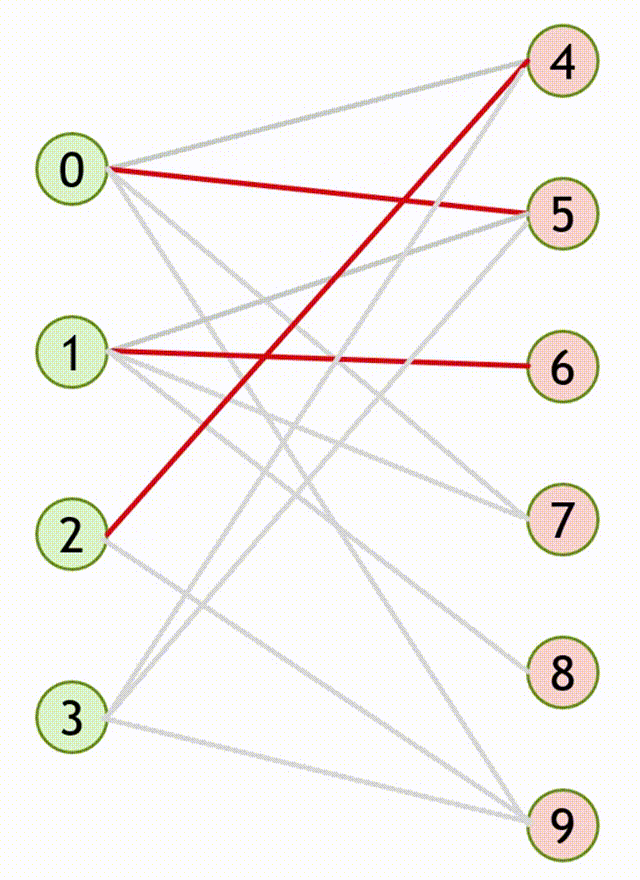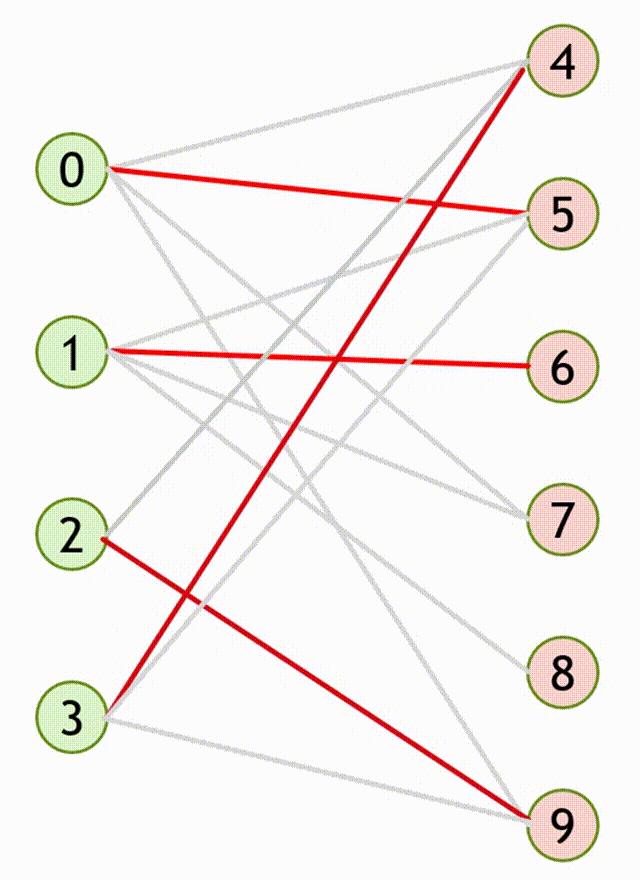
- 此时可以得到的增广路 \(path= \{ (x,y),(x',y') \}\) 。
- \(y\) 是非匹配点。
- 正确性基于贪心策略,其一个重要特点是:当一个节点成为匹配点后,至多因为找到增广路而更换匹配对象,但绝不会再变回非匹配点。
- 找到一条增广路后把路径上所有边的匹配状态取反,得到更大的匹配,直至图中不存在增广路。
- 时间复杂度为 \(O(nm)\) 。
点击查看代码
struct node { int nxt,to; }e[100010]; int head[100010],match[100010],vis[100010],cnt=0; void add(int u,int v) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt; } int dfs(int x,int flag) { for(int i=head[x];i!=0;i=e[i].nxt) { if(vis[e[i].to]!=flag)//减少因清空 vis 数组而带来的常数影响 { vis[e[i].to]=flag; if(match[e[i].to]==0||dfs(match[e[i].to],flag)==0) { match[e[i].to]=x; return 1; } } } return 1; } int main() { int nl,nr,m,u,v,ans=0,i; cin>>nl>>nr>>m; for(i=1;i<=m;i++) { cin>>u>>v; add(u,v); } for(i=1;i<=nl;i++) { ans+=dfs(i,i); } cout<<ans<<endl; return 0; } - 定义
牛客 NC52275 图的遍历
-
只要图中存在奇环,“走两步”就能遍历完整个图;否则需要加上一条边,使其存在奇环。
点击查看代码
struct node { int nxt,to; }e[200010]; int head[200010],vis[200010],cnt=0; void add(int u,int v) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt; } void dfs(int x,int col,int &sum) { vis[x]=col; for(int i=head[x];i!=0;i=e[i].nxt) { if(vis[e[i].to]==0) { dfs(e[i].to,3-col,sum); } if(vis[e[i].to]==col) { sum=0; } } } int main() { int n,m,u,v,ans=-1,sum=1,i; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; add(u,v); add(v,u); } for(i=1;i<=n;i++) { if(vis[i]==0) { dfs(i,1,sum); ans++; } } cout<<ans+sum<<endl; return 0; }
5.14
闲话
- 上午化学实验被现化学老师 \(D\) 了约 \(15min\) ,称我们安全意识和规则意识太淡薄,乱做实验,讲了下昨天一个同学被酒精灯烧着衣服了,一个同学被酒精灯烧着头发了。
- 中午原班主任来查寝,问我下次打算考多少名,还能再退步吗,我说估计不能再退了。
- 貌似又因为机房太吵,吵到了 \(huge\) ,又双叒叕被 \(D\) 了。
- 晚新闻的时候班里同学提醒“陶老头(代班主任)回家做饭去了,他说同学们上次考得太差了,这次要好好备考”。
做题纪要
luogu P5076 【深基16.例7】普通二叉树(简化版)
-
set维护即可。set迭代器不能相减,故遍历即可。
点击查看代码
set<int>s; set<int>::iterator it1,it2; int main() { ll m,pd,x,sum=0,i; cin>>m; s.insert(-2147483647); s.insert(2147483647); for(i=1;i<=m;i++) { cin>>pd>>x; if(pd==1) { sum=0; it1=s.lower_bound(x); for(it2=s.begin();it2!=it1;it2++) { sum++; } cout<<sum<<endl; } if(pd==2) { sum=0; for(it1=s.begin();sum!=x;it1++) { sum++; } cout<<*it1<<endl; } if(pd==3) { cout<<*(--s.lower_bound(x))<<endl; } if(pd==4) { cout<<*s.upper_bound(x)<<endl; } if(pd==5) { s.insert(x); } } return 0; }
luogu P3369 【模板】普通平衡树
- 多倍经验: luogu P6136 【模板】普通平衡树(数据加强版)
- 普通平衡树板子。
- 由于二叉搜索树有可能退化成链表,使得插入、删除、修改、查找等操作的时间复杂度退化成 \(O(n)\) 。
- 故引入平衡树的概念,通过一定操作维持树的高度(平衡性)来降低操作的复杂度。
- 常见的平衡性的定义是指以 \(root\) 为根节点的树,每一个节点的左子树和右子树的高度差最多为 \(1\) 。
- \(Treap\)
- \(Treap\) 是一种弱平衡的二叉搜索树。它同时满足二叉搜索树和堆的性质。
- 二叉搜索树性质: \(val_{lson(x)}<val_{x}<val_{rson(x)}\) 或 \(val_{lson(x)}>val_{x}>val_{rson(x)}\)
- 堆性质: \(priority_{son(x)}<priority_{x}\) 或 \(priority_{son(x)}>priority_{x}\)
- 对于 \(val\) 值,我们维护搜索树的性质,常在插入时维护;对于 \(priority\) 值,我们维护堆的性质,常见处理方法是旋转和分裂、合并,其中 \(priority\) 的值是随机给定的。
- 关于为什么建议 \(priority\) 的值是随机给定的建议看 OI Wiki 。
- 平衡的调整过程(保证中序遍历序列不变)
- 有旋 \(Treap\)
-
旋转
romate- 左旋/左单旋转/ \(RR\) 平衡旋转
left romate或zig- 对于节点 \(A\) 进行左旋时,先将 \(A\) 的右儿子 \(B\) 向左上旋转,代替 \(A\) 成为根节点;将 \(A\) 节点向左下旋转成为 \(B\) 的左子树的根节点,使得 \(B\) 原来的左子树变成 \(A\) 的右子树。
- 右旋/右单旋转/ \(LL\) 平衡旋转
right romate或zag- 对于节点 \(A\) 进行右旋时,先将 \(A\) 的左儿子 \(B\) 向右上旋转,代替 \(A\) 成为根节点;将 \(A\) 节点向右下旋转成为 \(B\) 的右子树的根节点,使得 \(B\) 原来的右子树变成 \(A\) 的左子树。
- 两种旋转方式归纳后得到在不影响性质的前提下,把和旋转方向 相反 的子树变成根节点;在旋转过后,和旋转方向 相同 的子节点是原来的根节点。
- 形如
,图来自 平衡的调整过程 。
- 左旋/左单旋转/ \(RR\) 平衡旋转
-
插入
insert- 类似线段树二分,注意的是在插的过程中通过旋转来维护堆的性质。
-
删除
del- 类似线段树二分,注意当要删除的节点有左子树和右子树的时候要维护堆的性质。
-
查询排名
query_rk- 当前根节点 \(x\) 为空时,说明要查询的点在平衡树中不存在,返回 \(1\) 。
-
第 \(k\) 小
kth_min- 类似线段树二分。
-
查前驱
query_pre- 类似线段树二分。
-
查后继
query_nxt- 类似线段树二分。
点击查看代码
const int INF=0x7f7f7f7f; int rt_sum=0; struct Treap { int son[2],val,rnd,cnt,siz; }tree[100010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) #define dson(rt,d) (tree[rt].son[d]) #define ason(rt,d) (tree[rt].son[d^1]) void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].val=val; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void rotate(int &rt,int d) { int lsrt=ason(rt,d); ason(rt,d)=dson(lsrt,d); dson(lsrt,d)=rt; pushup(rt); rt=lsrt; pushup(rt); } void insert(int &rt,int val) { if(rt==0)//没有则直接新建 { rt=build(val); } else { if(tree[rt].val==val) { tree[rt].cnt++; tree[rt].siz++; } else { int d=(val>tree[rt].val); insert(dson(rt,d),val);//维护搜索树性质 if(tree[rt].rnd<tree[dson(rt,d)].rnd)//维护堆性质 { rotate(rt,d^1);//相反方向 } pushup(rt); } } } void del(int &rt,int val) { if(rt==0)//没有则不管 { return; } else { if(tree[rt].val==val) { if(lson(rt)==0) { if(rson(rt)==0)//没有左右子树则不管 { tree[rt].cnt--; tree[rt].siz--; rt=(tree[rt].cnt==0)?0:rt;//删除节点 } else//有右无左 { rotate(rt,0); del(dson(rt,0),val);//旋转完成后原来的根节点是旋转方向的子节点,需要删除 } } else { if(rson(rt)==0)//有左无右 { rotate(rt,1); del(dson(rt,1),val);//旋转完成后原来的根节点是旋转方向的子节点,需要删除 } else { int d=(tree[lson(rt)].rnd<tree[rson(rt)].rnd); rotate(rt,d^1); del(dson(rt,d^1),val);//旋转完成后原来的根节点是旋转方向的子节点,需要删除 } } } else { int d=(val>tree[rt].val); del(dson(rt,d),val); } pushup(rt); } } int query_rk(int rt,int val) { if(rt==0) { return 1; } if(tree[rt].val<val) { return tree[lson(rt)].siz+tree[rt].cnt+query_rk(rson(rt),val); } else { if(tree[rt].val==val) { return tree[lson(rt)].siz+1; } else { return query_rk(lson(rt),val); } } } int kth_min(int rt,int k) { if(rt==0) { return 0; } if(k<=tree[lson(rt)].siz) { return kth_min(lson(rt),k); } if(tree[lson(rt)].siz+tree[rt].cnt<k) { return kth_min(rson(rt),k-tree[lson(rt)].siz-tree[rt].cnt); } else { return tree[rt].val; } } int query_pre(int rt,int val) { if(rt==0) { return -INF; } if(tree[rt].val<val) { return max(tree[rt].val,query_pre(rson(rt),val)); } else { return query_pre(lson(rt),val); } } int query_nxt(int rt,int val) { if(rt==0) { return INF; } if(tree[rt].val>val) { return min(tree[rt].val,query_nxt(lson(rt),val)); } else { return query_nxt(rson(rt),val); } } int main() { int m,pd,x,rt=0,i;//rt初始化为空节点 srand(time(0)); cin>>m; for(i=1;i<=m;i++) { cin>>pd>>x; if(pd==1) { insert(rt,x); } if(pd==2) { del(rt,x); } if(pd==3) { cout<<query_rk(rt,x)<<endl; } if(pd==4) { cout<<kth_min(rt,x)<<endl; } if(pd==5) { cout<<query_pre(rt,x)<<endl; } if(pd==6) { cout<<query_nxt(rt,x)<<endl; } } return 0; }
-
- 无旋 \(Treap\) / \(FHQ-Treap\)
-
无旋 \(Treap\) 中权值 \(val\) 相等的节点不再统一合并到一起。
-
分裂
split- 按权值分裂
- 将一棵平衡树拆成两棵,使得左边的树上节点的值都 \(\le val\) ,右边的树上节点的值都 \(>val\) ,其中 \(val\) 是给定的。
- 注意递归边界。
- 按子树大小/排名分裂
- 按权值分裂
-
合并
merge- 类似线段树合并。合并时由于两棵子树内部是有序的,故只需要考虑谁在上谁在下即可。
- 合并时只能是两个相邻的子树合并,不能跳着合并。
- 类似线段树合并。合并时由于两棵子树内部是有序的,故只需要考虑谁在上谁在下即可。
-
插入
insert- 将整棵子树分裂成 \(\le val\) 和 \(>val\) 两部分,新建一棵只有 \(val\) 一个节点的树,然后顺次合并。
-
删除
del- 将整棵子树分裂成 \(<val,=val,>val\) 三部分,删除 \(=val\) 的子树的根节点,然后顺次合并。
-
查询排名
query_rk- 将整棵子树分裂成 \(<val\) 和 \(\ge val\) 两部分,前者大小加 \(1\) 即为所求。
-
第 \(k\) 小
kth_min- 同有旋 \(Treap\) 。
-
查前驱
query_pre- 将整棵子树分裂成 \(<val\) 和 \(\ge val\) 两部分,前者最大的一个数即为所求。
-
查后继
query_nxt- 将整棵子树分裂成 \(\le val\) 和 \(>val\) 两部分,后者最小的一个数即为所求。
点击查看代码
struct BST { const int INF=0x7f7f7f7f; int rt_sum,root; struct FHQ_Treap { int son[2],val,rnd,cnt,siz; }tree[300010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) BST() { rt_sum=root=0; srand(time(0)); } int siz() { return tree[root].siz; } void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].val=val; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void split(int rt,int val,int &ls,int &rs) { if(rt==0) { ls=rs=0; return; } if(tree[rt].val<=val) { ls=rt;//左儿子全部满足 split(rson(ls),val,rson(ls),rs);//递归分裂右儿子 } else { rs=rt;//右儿子全部满足 split(lson(rs),val,ls,lson(rs));//递归分裂左儿子 } pushup(rt); } int merge(int rt1,int rt2) { if(rt1==0||rt2==0) { return rt1+rt2; } if(tree[rt1].rnd<tree[rt2].rnd) { rson(rt1)=merge(rson(rt1),rt2);//将 rt2 与 rt1 的右子树合并 pushup(rt1); return rt1; } else { lson(rt2)=merge(rt1,lson(rt2));//将 rt1 与 rt2 的左子树合并 pushup(rt2); return rt2; } } void insert(int val) { int ls,rs; split(root,val,ls,rs); root=merge(merge(ls,build(val)),rs); } void del(int val) { int ls,rs,rt; split(root,val,ls,rs); split(ls,val-1,ls,rt); root=merge(merge(ls,merge(lson(rt),rson(rt))),rs); } int query_rk(int val) { int ls,rs,ans; split(root,val-1,ls,rs); ans=tree[ls].siz+1; root=merge(ls,rs); return ans; } int kth_min(int rt,int k) { if(rt==0) { return 0; } if(k<=tree[lson(rt)].siz) { return kth_min(lson(rt),k); } else { if(tree[lson(rt)].siz+tree[rt].cnt<k) { return kth_min(rson(rt),k-tree[lson(rt)].siz-tree[rt].cnt); } else { return tree[rt].val; } } } int query_pre(int val) { int ls,rs,ans; split(root,val-1,ls,rs); ans=(ls==0)?-INF:kth_min(ls,tree[ls].siz);//边界处理 root=merge(ls,rs); return ans; } int query_nxt(int val) { int ls,rs,ans; split(root,val,ls,rs); ans=(rs==0)?INF:kth_min(rs,1);//边界处理 root=merge(ls,rs); return ans; } }T; int main() { int m,pd,x,i; cin>>m; for(i=1;i<=m;i++) { cin>>pd>>x; if(pd==1) { T.insert(x); } if(pd==2) { T.del(x); } if(pd==3) { cout<<T.query_rk(x)<<endl; } if(pd==4) { cout<<T.kth_min(T.root,x)<<endl; } if(pd==5) { cout<<T.query_pre(x)<<endl; } if(pd==6) { cout<<T.query_nxt(x)<<endl; } } return 0; }
-
- 有旋 \(Treap\)
- \(Treap\) 是一种弱平衡的二叉搜索树。它同时满足二叉搜索树和堆的性质。
- \(Splay\) 树/伸展树
-
\(Splay\) 树是一种平衡二叉搜索树,它通过 \(Splay\) /伸展操作不断将某个节点旋转至根节点,使得整棵树仍然满足二叉搜索树的性质。
- 单次时间复杂度均摊为 \(O(\log{n})\) ,详细分析过程看 OI Wiki 吧。
-
旋转
romate- 旋转过程和有旋 \(Treap\) 基本一致,但需要在旋转的过程中额外更改父亲。
- 此时去纠结旋转方向有些多余了,本质上是将某个节点上移一个位置。
- 形如
,图来自 平衡的调整过程 。
-
伸展
splaysplay(x,to)表示把 \(x\) 转到 \(to\) 的子节点上。特别地,有当 \(to=0\) 时,旋转到根节点。- 每访问一个节点 \(x\) 后都要将其强制旋转到根节点。
- 设当前节点为 \(x\) ,父亲为 \(y\) ,祖父为 \(z\) ,然后大力分讨。
-
查找
find- 由二叉搜索树性质,向左/右查找即可,查找后将其位置伸展到根节点。
-
插入
insert- 类似查找的过程,若能找到则直接修改,否则记录其父亲,新建节点。
-
查询排名
query_rk- 伸展后左子树大小加 \(1\) 即为所求。
- 为方便代码书写,事先将 \(-\infty,\infty\) 插入 \(Splay\) 树中,请时刻注意哨兵因此带来的影响。
-
第 \(k\) 小
kth_min- 同有旋 \(Treap\) 。
-
查前驱
query_pre- 伸展后,若根节点已经符合条件则直接返回,否则在左子树上一直向右走。
- 为方便代码书写,事先将 \(-\infty\) 插入 \(Splay\) 树中,请时刻注意哨兵因此带来的影响。
-
查后继
query_nxt- 伸展后,若根节点已经符合条件则直接返回,否则在左子树上一直向左走。
- 为方便代码书写,事先将 \(\infty\) 插入 \(Splay\) 树中,请时刻注意哨兵因此带来的影响。
-
删除
del- 先将 \(x\) 的前驱旋转到根,再把 \(x\) 的后继旋转到 \(x\) 的前驱的右儿子处,此时 \(x\) 就是 \(x\) 的后继的左儿子,删除影响即可。
点击查看代码
struct BST { const int INF=0x7f7f7f7f; int rt_sum,root; struct Splay { int son[2],fa,val,cnt,siz; }tree[300010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) #define dson(rt,d) (tree[rt].son[d]) #define ason(rt,d) (tree[rt].son[d^1]) BST() { rt_sum=root=0; insert(INF);//加入哨兵 insert(-INF); } int fdson(int rt) { return ((rt==lson(tree[rt].fa))?0:1); } void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val,int fa) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].fa=fa; tree[rt_sum].val=val; tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void rotate(int x) { int y=tree[x].fa,z=tree[y].fa,d=fdson(x); dson(z,fdson(y))=x;//z 原来 y 的位置变成 x tree[x].fa=z;//x 的父亲变成 z dson(y,d)=ason(x,d);//y 原来 x 的位置变成 x 的与 x 原来在 y 的相对的那个儿子 tree[ason(x,d)].fa=y;//更新父亲 ason(x,d)=y;//x 的与 x 原来在 y 的相对的那个儿子变成 y tree[y].fa=x;//更新父亲 pushup(y); pushup(x); } void splay(int x,int to) { while(tree[x].fa!=to) { int y=tree[x].fa,z=tree[y].fa; if(z!=to) { rotate((fdson(x)==fdson(y))?y:x); } rotate(x); } root=(to==0)?x:root; } void find(int val) { int rt=root; if(rt!=0)//保证树非空 { while(dson(rt,val>tree[rt].val)!=0&&tree[rt].val!=val) { rt=dson(rt,val>tree[rt].val); } splay(rt,0);//旋转到根节点 } } void insert(int val) { int rt=root,fa=0; while(rt!=0&&tree[rt].val!=val) { fa=rt;//记录父亲 rt=dson(rt,val>tree[rt].val); } if(rt==0) { rt=build(val,fa); if(fa!=0) { dson(fa,val>tree[fa].val)=rt; } } else { tree[rt].cnt++; } splay(rt,0); } int query_rk_INF(int val) { find(val); return tree[lson(root)].siz+1; } int query_rk(int val) { return query_rk_INF(val)-1;//减去哨兵影响 } int kth_min_INF(int rt,int k) { if(rt==0) { return 0; } if(k<=tree[lson(rt)].siz) { return kth_min_INF(lson(rt),k); } else { if(tree[lson(rt)].siz+tree[rt].cnt<k) { return kth_min_INF(rson(rt),k-tree[lson(rt)].siz-tree[rt].cnt); } else { return tree[rt].val; } } } int kth_min(int rt,int k) { return kth_min_INF(rt,k+1);//注意有哨兵 } int query_pre_idx(int val) { find(val);//找到并伸展到根节点 int rt=root;//val 的父亲(如果存在)就是根节点 if(tree[rt].val>=val)//若不存在 val 这个点,则找的是与 val 相近的点 { rt=lson(rt); while(rson(rt)!=0) { rt=rson(rt); } } return rt; } int query_pre(int val) { return tree[query_pre_idx(val)].val; } int query_nxt_idx(int val) { find(val); int rt=root; if(tree[rt].val<=val) { rt=rson(rt); while(lson(rt)!=0) { rt=lson(rt); } } return rt; } int query_nxt(int val) { return tree[query_nxt_idx(val)].val; } void del(int val) { int pre=query_pre_idx(val),nxt=query_nxt_idx(val); splay(pre,0); splay(nxt,pre); if(tree[lson(nxt)].cnt<=1) { lson(nxt)=0; } else { tree[lson(nxt)].cnt--; splay(lson(nxt),0); } } }T; int main() { int m,pd,x,i; cin>>m; for(i=1;i<=m;i++) { cin>>pd>>x; if(pd==1) { T.insert(x); } if(pd==2) { T.del(x); } if(pd==3) { T.insert(x);//为防止 find 出错事先将 x 插进去 cout<<T.query_rk(x)<<endl; T.del(x);//删除 x } if(pd==4) { cout<<T.kth_min(T.root,x)<<endl; } if(pd==5) { cout<<T.query_pre(x)<<endl; } if(pd==6) { cout<<T.query_nxt(x)<<endl; } } return 0; }
-
5.15
闲话
- 物理实验时 @wkh2008 的“以蜡制蜡”工艺得到很大进展。
- 中午和 @远远大可爱 闲聊了下,他说他们当时给奥赛生的政策是降分,不像我们是直接直升(但不保证学费)。
- \(field\) 带队去打 \(APIO\) 了,和 \(miaomiao\) 直接会和。 \(huge\) 休假了,机房里只剩下了 \(feifei\) 。
- 晚二本来是数学自习(因为实验课占了上午的数学课,改到了晚上),但现数学老师昨天下午第 \(6\) 节已经上了,所以晚二改奥赛自习了,到机房后找 \(feifei\) 沟通了下让晚三也改奥赛自习了。
- 详见 2024 HE中考 游记 5.15 。
做题纪要
luogu P2234 [HNOI2002] 营业额统计
-
找到 \(<a_{i}\) 和 \(\ge a_{i}\) 的取 \(\min\) 即可。
点击查看代码
const int INF=0x7f7f7f7f; int rt_sum=0; struct Treap { int son[2],val,rnd,cnt,siz; }tree[400000]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) #define dson(rt,d) (tree[rt].son[d]) #define ason(rt,d) (tree[rt].son[d^1]) void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].val=val; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void rotate(int &rt,int d) { int lsrt=ason(rt,d); ason(rt,d)=dson(lsrt,d); dson(lsrt,d)=rt; pushup(rt); rt=lsrt; pushup(rt); } void insert(int &rt,int val) { if(rt==0) { rt=build(val); } else { if(tree[rt].val==val) { tree[rt].cnt++; tree[rt].siz++; } else { int d=(val>tree[rt].val); insert(dson(rt,d),val); if(tree[rt].rnd<tree[dson(rt,d)].rnd) { rotate(rt,d^1); } pushup(rt); } } } int query_pre(int rt,int val) { if(rt==0) { return -INF; } if(tree[rt].val<val) { return max(tree[rt].val,query_pre(rson(rt),val)); } else { return query_pre(lson(rt),val); } } int query_lower(int rt,int val) { if(rt==0) { return INF; } if(tree[rt].val>=val) { return min(tree[rt].val,query_lower(lson(rt),val)); } else { return query_lower(rson(rt),val); } } int main() { int n,x,ans=0,rt=0,i; srand(time(0)); cin>>n; for(i=1;i<=n;i++) { cin>>x; ans+=((i==1)?x:min(x-query_pre(rt,x),query_lower(rt,x)-x)); insert(rt,x); } cout<<ans<<endl; return 0; }
luogu P2286 [HNOI2004] 宠物收养场
-
两个平衡树不太写,考虑直接封装。
点击查看代码
const ll p=1000000; struct BST { const ll INF=0x7f7f7f7f; ll rt_sum,root; struct Treap { ll son[2],val,rnd,cnt,siz; }tree[100010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) #define dson(rt,d) (tree[rt].son[d]) #define ason(rt,d) (tree[rt].son[d^1]) BST() { rt_sum=root=0; srand(time(0));//虽说第一次调用会被第二次覆盖,但无伤大雅 } void pushup(ll rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } ll build(ll val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].val=val; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void rotate(ll &rt,ll d) { ll lsrt=ason(rt,d); ason(rt,d)=dson(lsrt,d); dson(lsrt,d)=rt; pushup(rt); rt=lsrt; pushup(rt); } void insert(ll &rt,ll val) { if(rt==0) { rt=build(val); } else { if(tree[rt].val==val) { tree[rt].cnt++; tree[rt].siz++; } else { ll d=(val>tree[rt].val); insert(dson(rt,d),val); if(tree[rt].rnd<tree[dson(rt,d)].rnd) { rotate(rt,d^1); } pushup(rt); } } } void del(ll &rt,ll val) { if(rt==0) { return; } else { if(tree[rt].val==val) { if(lson(rt)==0) { if(rson(rt)==0) { tree[rt].cnt--; tree[rt].siz--; rt=(tree[rt].cnt==0)?0:rt; } else { rotate(rt,0); del(dson(rt,0),val); } } else { if(rson(rt)==0) { rotate(rt,1); del(dson(rt,1),val); } else { ll d=(tree[lson(rt)].rnd<tree[rson(rt)].rnd); rotate(rt,d^1); del(dson(rt,d^1),val); } } } else { ll d=(val>tree[rt].val); del(dson(rt,d),val); } pushup(rt); } } ll query_pre(ll rt,ll val) { if(rt==0) { return -INF; } if(tree[rt].val<val) { return max(tree[rt].val,query_pre(rson(rt),val)); } else { return query_pre(lson(rt),val); } } ll query_lower(ll rt,ll val) { if(rt==0) { return INF; } if(tree[rt].val>=val) { return min(tree[rt].val,query_lower(lson(rt),val)); } else { return query_lower(rson(rt),val); } } ll siz() { return tree[root].siz; } }pet,per; int main() { ll n,pd,x,ans=0,sum1,sum2,i; cin>>n; for(i=1;i<=n;i++) { cin>>pd>>x; if(pd==0) { if(per.siz()==0) { pet.insert(pet.root,x); } else { sum1=per.query_pre(per.root,x); sum2=per.query_lower(per.root,x); if(x-sum1<=sum2-x) { ans=(ans+(x-sum1)%p)%p; per.del(per.root,sum1); } else { ans=(ans+(sum2-x)%p)%p; per.del(per.root,sum2); } } } else { if(pet.siz()==0) { per.insert(per.root,x); } else { sum1=pet.query_pre(pet.root,x); sum2=pet.query_lower(pet.root,x); if(x-sum1<=sum2-x) { ans=(ans+(x-sum1)%p)%p; pet.del(pet.root,sum1); } else { ans=(ans+(sum2-x)%p)%p; pet.del(pet.root,sum2); } } } } cout<<ans<<endl; return 0; }
5.16
闲话
- 早读在课代表没有提前通知的情况下放了维克多听力,而且貌似早读下课时间往后延了,昨天化奥教练也没说,听完听力直接来机房了。
- \(miaomiao\) 回来了,还问我们什么时候停上奥赛课,我们说等考完二模,又问我们这周放假吗。
做题纪要
luogu P1486 [NOI2004] 郁闷的出纳员
-
对于全局修改维护一个懒标记 \(lazy_{x}\) 。
-
插入时将 \(k-lazy_{i}\) 插入平衡树中;删除时直接删除 \(< \min-lazy_{i}\) 的整棵子树即可;查询第 \(k\) 大时加上 \(lazy_{i}\) 。
点击查看代码
struct BST { const int INF=0x7f7f7f7f; int rt_sum,root; struct FHQ_Treap { int son[2],val,rnd,cnt,siz; }tree[300010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) BST() { rt_sum=root=0; srand(time(0)); } int siz(int rt) { return tree[rt].siz; } void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].val=val; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void split(int rt,int val,int &ls,int &rs) { if(rt==0) { ls=rs=0; return; } if(tree[rt].val<=val) { ls=rt; split(rson(ls),val,rson(ls),rs); } else { rs=rt; split(lson(rs),val,ls,lson(rs)); } pushup(rt); } int merge(int rt1,int rt2) { if(rt1==0||rt2==0) { return rt1+rt2; } if(tree[rt1].rnd<tree[rt2].rnd) { rson(rt1)=merge(rson(rt1),rt2); pushup(rt1); return rt1; } else { lson(rt2)=merge(rt1,lson(rt2)); pushup(rt2); return rt2; } } void insert(int val) { int ls,rs; split(root,val,ls,rs); root=merge(merge(ls,build(val)),rs); } void del(int val) { int ls,rs,rt; split(root,val,ls,rs); split(ls,val-1,ls,rt); root=merge(merge(ls,merge(lson(rt),rson(rt))),rs); } int kth_min(int rt,int k) { if(rt==0) { return 0; } if(k<=tree[lson(rt)].siz) { return kth_min(lson(rt),k); } else { if(tree[lson(rt)].siz+tree[rt].cnt<k) { return kth_min(rson(rt),k-tree[lson(rt)].siz-tree[rt].cnt); } else { return tree[rt].val; } } } int kth_max(int rt,int k) { return kth_min(rt,siz(rt)-k+1); } }T; int main() { int n,m,lazy=0,x,ans=0,i; char pd; cin>>n>>m; for(i=1;i<=n;i++) { cin>>pd>>x; if(pd=='I') { if(x>=m) { T.insert(x-lazy); } } if(pd=='A') { lazy+=x; } if(pd=='S') { lazy-=x; int ls,rs; T.split(T.root,m-lazy-1,ls,rs); T.root=rs; ans+=T.siz(ls); } if(pd=='F') { cout<<((x<=T.siz(T.root))?T.kth_max(T.root,x)+lazy:-1)<<endl; } } cout<<ans<<endl; return 0; }
luogu P3391 【模板】文艺平衡树
- \(FHQ-Treap\)
- \(FHQ-Treap\) 便于实现各种区间操作。
- 将下标顺序插入 \(Treap\) 中,此时 \(Treap\) 的中序遍历就是原区间。
- 记录懒标记表示是否需要把每一个子节点交换位置,注意两次翻转可以抵消。
- 分裂
split- 由于区间翻转操作的存在,按照权值分裂不再满足二叉搜索树的性质,所以选择按照子树大小/排名分裂。
- 将一棵平衡树拆成两棵,使得左边的树上节点的子树大小/排名都 \(\le k\) ,右边的树上节点的子树大小/排名都 \(>k\) ,其中 \(k\) 是给定的。
- 需要下传懒标记。
- 合并
merge- 需要下传懒标记。
- 区间翻转
reverse- 将平衡树分裂成 \([1,l),[l,r],(r,n)\) 三部分,对 \([l,r]\) 打标记。
- 中序遍历
inorder-
遍历顺序为“左根右”。
-
需要下传懒标记。
点击查看代码
struct BST { const int INF=0x7f7f7f7f; int rt_sum,root; struct FHQ_Treap { int son[2],val,rnd,cnt,siz,lazy; }tree[100010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) BST() { rt_sum=root=0; srand(time(0)); } void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=tree[rt_sum].lazy=0; tree[rt_sum].val=val; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void pushdown(int rt) { if(rt!=0&&tree[rt].lazy!=0)//注意空节点不能转 { swap(lson(rt),rson(rt)); tree[lson(rt)].lazy^=1; tree[rson(rt)].lazy^=1; tree[rt].lazy=0; } } void split(int rt,int k,int &ls,int &rs) { if(rt==0) { ls=rs=0; return; } pushdown(rt); if(tree[lson(rt)].siz+tree[rt].cnt<=k) { ls=rt; split(rson(ls),k-tree[lson(rt)].siz-tree[rt].cnt,rson(ls),rs); } else { rs=rt; split(lson(rs),k,ls,lson(rs)); } pushup(rt); } int merge(int rt1,int rt2) { if(rt1==0||rt2==0) { return rt1+rt2; } if(tree[rt1].rnd<tree[rt2].rnd) { pushdown(rt1); rson(rt1)=merge(rson(rt1),rt2); pushup(rt1); return rt1; } else { pushdown(rt2); lson(rt2)=merge(rt1,lson(rt2)); pushup(rt2); return rt2; } } void insert(int val) { int ls,rs; split(root,val,ls,rs); root=merge(merge(ls,build(val)),rs); } void reverse(int l,int r) { int ls,rs,mid; split(root,r,ls,rs); split(ls,l-1,ls,mid); tree[mid].lazy^=1; root=merge(merge(ls,mid),rs); } void inorder(int rt) { if(rt!=0) { pushdown(rt); inorder(lson(rt)); cout<<tree[rt].val<<" "; inorder(rson(rt)); } } }T; int main() { int n,m,l,r,i; cin>>n>>m; for(i=1;i<=n;i++) { T.insert(i); } for(i=1;i<=m;i++) { cin>>l>>r; T.reverse(l,r); } T.inorder(T.root); return 0; }
-
- \(Splay\) 树/伸展树
- 类似 \(FHQ-Treap\) , \(Splay\) 树同样便于实现各种区间操作。
- 将下标顺序插入 \(Splay\) 树中,此时 \(Splay\) 树的中序遍历就是原区间。
- 第 \(k\) 小所在位置
kth_min_idx- 对
kth_min稍作修改即可。 - 需要下传懒标记。
- 对
- 分裂
split- 类似删除操作,将第 \(l-1\) 小所在的位置旋转到根,将第 \(r+1\) 小所在的位置旋转到前者的右儿子上,此时后者的左儿树即为 \([l,r]\) 。
- 翻转
reverse- 分裂出区间后打标记即可。
- 中序遍历
inorder-
遍历顺序为“左根右”。
-
需要下传懒标记。
点击查看代码
struct BST { const int INF=0x7f7f7f7f; int rt_sum,root; struct Splay { int son[2],fa,val,cnt,siz,lazy; }tree[100010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) #define dson(rt,d) (tree[rt].son[d]) #define ason(rt,d) (tree[rt].son[d^1]) BST() { rt_sum=root=0; insert(INF); insert(-INF); } int fdson(int rt) { return ((rt==lson(tree[rt].fa))?0:1); } void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val,int fa) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].fa=fa; tree[rt_sum].val=val; tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void pushdown(int rt) { if(rt!=0&&tree[rt].lazy!=0)//注意空节点不能转 { swap(lson(rt),rson(rt)); tree[lson(rt)].lazy^=1; tree[rson(rt)].lazy^=1; tree[rt].lazy=0; } } void rotate(int x) { int y=tree[x].fa,z=tree[y].fa,d=fdson(x); dson(z,fdson(y))=x; tree[x].fa=z; dson(y,d)=ason(x,d); tree[ason(x,d)].fa=y; ason(x,d)=y; tree[y].fa=x; pushup(y); pushup(x); } void splay(int x,int to) { while(tree[x].fa!=to) { int y=tree[x].fa,z=tree[y].fa; if(z!=to) { rotate((fdson(x)==fdson(y))?y:x); } rotate(x); } root=(to==0)?x:root; } void insert(int val) { int rt=root,fa=0; while(rt!=0&&tree[rt].val!=val) { fa=rt; rt=dson(rt,val>tree[rt].val); } if(rt==0) { rt=build(val,fa); if(fa!=0) { dson(fa,val>tree[fa].val)=rt; } } else { tree[rt].cnt++; } splay(rt,0); } int kth_min_idx_INF(int rt,int k) { pushdown(rt); if(rt==0) { return 0; } if(k<=tree[lson(rt)].siz) { return kth_min_idx_INF(lson(rt),k); } else { if(tree[lson(rt)].siz+tree[rt].cnt<k) { return kth_min_idx_INF(rson(rt),k-tree[lson(rt)].siz-tree[rt].cnt); } else { return rt; } } } int kth_min_idx(int rt,int k) { return kth_min_idx_INF(rt,k+1); } int split(int l,int r) { l=kth_min_idx(root,l-1); r=kth_min_idx(root,r+1); splay(l,0); splay(r,l); return lson(rson(l));//因为有翻转操作,所以不能直接写成 lson(r) } void reverse(int l,int r) { tree[split(l,r)].lazy^=1; } void inorder(int rt,int n) { if(rt!=0) { pushdown(rt); inorder(lson(rt),n); if(1<=tree[rt].val&&tree[rt].val<=n)//判断哨兵 { cout<<tree[rt].val<<" "; } inorder(rson(rt),n); } } }T; int main() { int n,m,l,r,i; cin>>n>>m; for(i=1;i<=n;i++) { T.insert(i); } for(i=1;i<=m;i++) { cin>>l>>r; T.reverse(l,r); } T.inorder(T.root,n); return 0; }
-
5.17
闲话
- 早饭听 @xrlong 讲了下夏令营和 \(APIO\) 教练带队情况: \(miaomiao\) 先去夏令营,然后 \(field\) 去 \(APIO\) ,和 \(miaomiao\) 会和后(可能不会和), \(miaomiao\) 就回学校了。
- 貌似只有昨天早读下课时间向后延了,今天正常点下课。
- 上午去机房的路上, @HANGRY_sol 称机房楼底下的石貔貅(公母未知)非常可爱,他非常喜欢。
- 化学课现化学老师不在,请的其他化学老师来代课,感觉有点不适应讲题前先讲知识点。
- 语文课现语文老师请的我初一语文老师来讲课,她负责听课,爆了不少典,“爱吃不吃,不吃滚出去”
- 语文自习课件说让写
综合作业,但课代表发的是复习作业,但以前这种事情多了,遂直接写了。 - 下午起床后遇见了 @iCostalymh ,和他闲聊了会儿,他建议我们先把高中数学学完,还谈到了选修三的概率期望。
- 详见 2024 HE中考 游记 5.17 。
- 晚二是物理实验,现物理老师忘提醒带物理课本了,到了之后发现隔壁教室是原班在做实验,索性直接找他们借了一本;桌子上电池充足,还有发光二极管,连了个发光二极管玩玩。
- 晚三发现班主任开完会回来了,传达了下年级部的要求,包括但不限于明天早上高三有活动,所以起了床直接去吃饭,让 \(6:50\) 在班进入状态。
做题纪要
luogu P3380 【模板】树套树
- 树套树板子。
- 线段树套平衡树
-
对于外层线段树正常建树,对于线段树上的每一个节点均建立一棵平衡树包含该节点所覆盖的序列。
- 在不垃圾回收的情况下,时间复杂度为 \(O((n+m)\log{n})\) 。
-
建树
build- 将覆盖的序列元素一个个插入平衡树中。
-
查询排名
query_rk- 由于线段树将区间拆开了,所以转为求区间内 \(<val\) 的个数,平衡树维护即可,然后加 \(1\) 即为所求。
-
第 \(k\) 小
kth_min- 二分维护即可。
-
修改
update- 将原下标所处的所有平衡树将原数删去,后将改后的数插入,自上而下递归即可,
-
查前驱
query_pre- 各个区间取 \(\max\) 即可。
-
查后继
query_nxt- 各个区间取 \(\min\) 即可。
点击查看代码
int a[50010]; struct BST { const int INF=2147483647; int rt_sum,root; struct FHQ_Treap { int son[2],val,rnd,cnt,siz; }tree[4000010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) BST() { rt_sum=root=0; srand(time(0)); } void pushup(int rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; } int build(int val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].val=val; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; return rt_sum; } void split(int rt,int val,int &ls,int &rs) { if(rt==0) { ls=rs=0; return; } if(tree[rt].val<=val) { ls=rt; split(rson(ls),val,rson(ls),rs); } else { rs=rt; split(lson(rs),val,ls,lson(rs)); } pushup(rt); } int merge(int rt1,int rt2) { if(rt1==0||rt2==0) { return rt1+rt2; } if(tree[rt1].rnd<tree[rt2].rnd) { rson(rt1)=merge(rson(rt1),rt2); pushup(rt1); return rt1; } else { lson(rt2)=merge(rt1,lson(rt2)); pushup(rt2); return rt2; } } void insert(int &rt,int val) { int ls,rs; split(rt,val,ls,rs); rt=merge(merge(ls,build(val)),rs); } void del(int &rt,int val) { int ls,rs,mid; split(rt,val,ls,rs); split(ls,val-1,ls,mid); rt=merge(merge(ls,merge(lson(mid),rson(mid))),rs); } int query_lsum(int rt,int val) { int ls,rs,ans; split(rt,val-1,ls,rs); ans=tree[ls].siz; rt=merge(ls,rs); return ans; } int kth_min(int rt,int k) { if(rt==0) { return 0; } if(k<=tree[lson(rt)].siz) { return kth_min(lson(rt),k); } else { if(tree[lson(rt)].siz+tree[rt].cnt<k) { return kth_min(rson(rt),k-tree[lson(rt)].siz-tree[rt].cnt); } else { return tree[rt].val; } } } int query_pre(int rt,int val) { int ls,rs,ans; split(rt,val-1,ls,rs); ans=(ls==0)?-INF:kth_min(ls,tree[ls].siz); rt=merge(ls,rs); return ans; } int query_nxt(int rt,int val) { int ls,rs,ans; split(rt,val,ls,rs); ans=(rs==0)?INF:kth_min(rs,1); rt=merge(ls,rs); return ans; } #undef lson #undef rson }B; struct SMT { const int INF=2147483647; struct SegmentTree { int l,r,root; }tree[200010]; int lson(int x) { return x*2; } int rson(int x) { return x*2+1; } void build(int rt,int l,int r) { tree[rt].l=l; tree[rt].r=r; tree[rt].root=0; for(int i=l;i<=r;i++) { B.insert(tree[rt].root,a[i]); } if(l==r) { return; } int mid=(l+r)/2; build(lson(rt),l,mid); build(rson(rt),mid+1,r); } void update(int rt,int pos,int val) { B.del(tree[rt].root,a[pos]); B.insert(tree[rt].root,val); if(tree[rt].l==tree[rt].r) { return; } int mid=(tree[rt].l+tree[rt].r)/2; if(pos<=mid) { update(lson(rt),pos,val); } else { update(rson(rt),pos,val); } } int query_lsum(int rt,int x,int y,int val) { if(x<=tree[rt].l&&tree[rt].r<=y) { return B.query_lsum(tree[rt].root,val); } int mid=(tree[rt].l+tree[rt].r)/2,ans=0; if(x<=mid) { ans+=query_lsum(lson(rt),x,y,val); } if(y>mid) { ans+=query_lsum(rson(rt),x,y,val); } return ans; } int query_rk(int x,int y,int val) { return query_lsum(1,x,y,val)+1; } int kth_min(int x,int y,int k) { int l=-100000000,r=100000000,mid,ans=INF; while(l<=r) { mid=(l+r)/2; if(query_rk(x,y,mid)<=k) { ans=mid; l=mid+1; } else { r=mid-1; } } return ans; } int query_pre(int rt,int x,int y,int val) { if(x<=tree[rt].l&&tree[rt].r<=y) { return B.query_pre(tree[rt].root,val); } int mid=(tree[rt].l+tree[rt].r)/2,ans=-INF; if(x<=mid) { ans=max(ans,query_pre(lson(rt),x,y,val)); } if(y>mid) { ans=max(ans,query_pre(rson(rt),x,y,val)); } return ans; } int query_nxt(int rt,int x,int y,int val) { if(x<=tree[rt].l&&tree[rt].r<=y) { return B.query_nxt(tree[rt].root,val); } int mid=(tree[rt].l+tree[rt].r)/2,ans=INF; if(x<=mid) { ans=min(ans,query_nxt(lson(rt),x,y,val)); } if(y>mid) { ans=min(ans,query_nxt(rson(rt),x,y,val)); } return ans; } }S; int main() { int n,m,pd,l,r,val,i; cin>>n>>m; for(i=1;i<=n;i++) { cin>>a[i]; } S.build(1,1,n); for(i=1;i<=m;i++) { cin>>pd; if(pd==1) { cin>>l>>r>>val; cout<<S.query_rk(l,r,val)<<endl; } if(pd==2) { cin>>l>>r>>val; cout<<S.kth_min(l,r,val)<<endl; } if(pd==3) { cin>>l>>val; S.update(1,l,val); a[l]=val; } if(pd==4) { cin>>l>>r>>val; cout<<S.query_pre(1,l,r,val)<<endl; } if(pd==5) { cin>>l>>r>>val; cout<<S.query_nxt(1,l,r,val)<<endl; } } return 0; }
-
- 线段树套平衡树
5.18
闲话
- 早上像往常一样,起床后直接跑向操场,跑到 \(9\) 号楼突然意识到不用跑操。
- 临到 \(6:50\) 的时候才到教室,然后现班主任交代了些东西,说下午体活的时候把我们叫回来。
- 物理实验连接了 \(11\) 节电池进行电解水,现物理老师就坐在面前看着我们做,瑞平“显得你会做是吧”。
- 数学课现数学老师提问了初二 \(20\) 班的三个同学(有我)对答案,都没写,然后 \(D\) 了我们;然后 我, @Pursuing_OIer , @wang54321 和 @lty_ylzsx 不知道为啥就被通报称“交流”了,现数学老师也很懵逼。现班主任没来处理我们,估计也没理由处理我们。
- 化学实验到了后因不会将滤纸叠成盒形,用大滤纸称量氯化钠被 \(D\) 了。
- 中午听 @Vsinger_洛天依 说 【数据删除】 改回来了。
- 详见 2024 HE中考 游记 5.18 。
- 下午 \(miaomiao\) 对 @minecraft418 的, @Vsinger_洛天依 的, @HS_xh 的和 @CuFeO4 旁边的电脑开了又关,关了又开,不知道在干啥。
- 体活的时候现班主任给 \(miaomiao\) 打电话,声音特别大,听到 \(miaomiao\) 说“周六最后一节课不是奥赛吗”,然后就把我们叫回去了。回班后,现班主任已经念完课表了,然后说了些近几天的东西。
- @HS_xh 电脑网被关了,然后听他说 【数据删除】 又给改回去了。
做题纪要
5.19
闲话
- 因为明天要实验中考,所以补的是周一的课。相应的周测也挪到了明天。
- 历史课,现历史老师开玩笑称我们昨天体活有人去打球了,所以停掉我们以后的体活,然后我们提醒他下周没有体活而且也要回原班了,同时和他说如果不让我们回原班那么停掉我们以后的体活也无所谓。
- 下午第 \(10\) 节课改成化学实验了,从机房出来路过教学楼的时候遇见现班主任和数奥教练了,到了实验室发现现化学老师又请假了。做实验的时候因我和 @Charlie_ljk 贪玩,直接把漏斗平着放到了桌子上,然后漏斗就掉到了地上摔碎了,简单收拾后去前面混了个新的。
- 详见 2024 HE中考 游记 5.19 。
做题纪要
luogu P2146 [NOI2015] 软件包管理器
-
路径修改、路径查询、子树修改、子树查询板子。
点击查看代码
struct node { int nxt,to; }e[100010]; int head[100010],c[100010],cc[100010],siz[100010],fa[100010],dep[100010],son[100010],top[100010],dfn[100010],out[100010],cnt=0,tot=0; struct SMT { struct SegmentTree { int l,r,sum,lazy; }tree[400010]; int lson(int x) { return x*2; } int rson(int x) { return x*2+1; } void pushup(int rt) { tree[rt].sum=tree[lson(rt)].sum+tree[rson(rt)].sum; } void build(int rt,int l,int r) { tree[rt].l=l; tree[rt].r=r; tree[rt].lazy=-1; if(l==r) { tree[rt].sum=cc[l]; return; } int mid=(l+r)/2; build(lson(rt),l,mid); build(rson(rt),mid+1,r); pushup(rt); } void pushdown(int rt) { if(tree[rt].lazy!=-1) { tree[lson(rt)].sum=tree[rt].lazy*(tree[lson(rt)].r-tree[lson(rt)].l+1); tree[rson(rt)].sum=tree[rt].lazy*(tree[rson(rt)].r-tree[rson(rt)].l+1); tree[lson(rt)].lazy=tree[rt].lazy; tree[rson(rt)].lazy=tree[rt].lazy; tree[rt].lazy=-1; } } void update(int rt,int x,int y,int val) { if(x<=tree[rt].l&&tree[rt].r<=y) { tree[rt].sum=val*(tree[rt].r-tree[rt].l+1); tree[rt].lazy=val; return; } pushdown(rt); int mid=(tree[rt].l+tree[rt].r)/2; if(x<=mid) { update(lson(rt),x,y,val); } if(y>mid) { update(rson(rt),x,y,val); } pushup(rt); } int query(int rt,int x,int y) { if(x<=tree[rt].l&&tree[rt].r<=y) { return tree[rt].sum; } pushdown(rt); int mid=(tree[rt].l+tree[rt].r)/2,ans=0; if(x<=mid) { ans+=query(lson(rt),x,y); } if(y>mid) { ans+=query(rson(rt),x,y); } return ans; } }T; void add(int u,int v) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt; } void dfs1(int x,int father) { siz[x]=1; fa[x]=father; dep[x]=dep[father]+1; for(int i=head[x];i!=0;i=e[i].nxt) { dfs1(e[i].to,x); siz[x]+=siz[e[i].to]; son[x]=(siz[e[i].to]>siz[son[x]])?e[i].to:son[x]; } } void dfs2(int x,int father,int id) { top[x]=id; tot++; dfn[x]=tot; cc[tot]=c[x]; if(son[x]!=0) { dfs2(son[x],x,id); for(int i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=son[x]) { dfs2(e[i].to,x,e[i].to); } } } out[x]=tot; } void update1(int u,int v,int val) { while(top[u]!=top[v]) { if(dep[top[u]]>dep[top[v]]) { T.update(1,dfn[top[u]],dfn[u],val); u=fa[top[u]]; } else { T.update(1,dfn[top[v]],dfn[v],val); v=fa[top[v]]; } } if(dep[u]<dep[v]) { T.update(1,dfn[u],dfn[v],val); } else { T.update(1,dfn[v],dfn[u],val); } } int query1(int u,int v) { int ans=0; while(top[u]!=top[v]) { if(dep[top[u]]>dep[top[v]]) { ans+=T.query(1,dfn[top[u]],dfn[u]); u=fa[top[u]]; } else { ans+=T.query(1,dfn[top[v]],dfn[v]); v=fa[top[v]]; } } if(dep[u]<dep[v]) { ans+=T.query(1,dfn[u],dfn[v]); } else { ans+=T.query(1,dfn[v],dfn[u]); } return ans; } void update2(int pos,int val) { T.update(1,dfn[pos],out[pos],val); } int query2(int pos) { return T.query(1,dfn[pos],out[pos]); } int main() { int n,m,u,v,sum1,sum2,i; string pd; cin>>n; for(i=2;i<=n;i++) { cin>>u; u++; v=i; add(u,v); } dfs1(1,0); dfs2(1,0,1); T.build(1,1,n); cin>>m; for(i=1;i<=m;i++) { cin>>pd>>u; u++; if(pd=="install") { sum1=query1(u,1); update1(u,1,1); sum2=query1(u,1); cout<<sum2-sum1<<endl; } else { sum1=query2(u); update2(u,0); sum2=query2(u); cout<<sum1-sum2<<endl; } } return 0; }
luogu P4036 [JSOI2008] 火星人
-
\(LCQ\) 可以通过二分哈希得到。
-
由于需要动态插入考虑类似 luogu P3391 【模板】文艺平衡树 的写法,让平衡树维护序列下标,但涉及到下标统一向右移问题,代之以子树大小来维护。
-
类似 [ABC331F] Palindrome Query ,平衡树在
pushup时顺便维护哈希值。点击查看代码
const ull base=13331; ull jc[300010]; char s[300010]; struct BST { const ll INF=0x7f7f7f7f; ll rt_sum,root; struct FHQ_Treap { ll son[2],rnd,cnt,siz; ull val,hsh; }tree[300010]; #define lson(rt) (tree[rt].son[0]) #define rson(rt) (tree[rt].son[1]) BST() { rt_sum=root=0; srand(time(0)); } void pushup(ll rt) { tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt; tree[rt].hsh=tree[lson(rt)].hsh*jc[tree[rson(rt)].siz+tree[rt].cnt]+tree[rt].val*jc[tree[rson(rt)].siz]+tree[rson(rt)].hsh; } ll build(ll val) { rt_sum++; lson(rt_sum)=rson(rt_sum)=0; tree[rt_sum].rnd=rand(); tree[rt_sum].cnt=tree[rt_sum].siz=1; tree[rt_sum].val=tree[rt_sum].hsh=val; return rt_sum; } void split(ll rt,ll k,ll &ls,ll &rs) { if(rt==0) { ls=rs=0; return; } if(tree[lson(rt)].siz+tree[rt].cnt<=k) { ls=rt; split(rson(ls),k-tree[lson(rt)].siz-tree[rt].cnt,rson(ls),rs); } else { rs=rt; split(lson(rs),k,ls,lson(rs)); } pushup(rt); } ll merge(ll rt1,ll rt2) { if(rt1==0||rt2==0) { return rt1+rt2; } if(tree[rt1].rnd<tree[rt2].rnd) { rson(rt1)=merge(rson(rt1),rt2); pushup(rt1); return rt1; } else { lson(rt2)=merge(rt1,lson(rt2)); pushup(rt2); return rt2; } } void insert(ll pos,ll val) { ll ls,rs; split(root,pos,ls,rs); root=merge(merge(ls,build(val)),rs); } void update(ll pos,ll val) { ll ls,rs,mid; split(root,pos,ls,rs); split(ls,pos-1,ls,mid); tree[mid].val=tree[mid].hsh=val; root=merge(merge(ls,mid),rs); } ull query(ll l,ll r) { ll ls,rs,mid; ull ans; split(root,r,ls,rs); split(ls,l-1,ls,mid); ans=tree[mid].hsh; root=merge(merge(ls,mid),rs); return ans; } }T; bool check(ll mid,ll l,ll r) { return (T.query(l,l+mid-1)==T.query(r,r+mid-1)); } ll query_lcp(ll len,ll x,ll y) { if(x>y) { swap(x,y); } ll l=0,r=len-y+1,mid,ans=0; while(l<=r) { mid=(l+r)/2; if(check(mid,x,y)==true) { ans=mid; l=mid+1; } else { r=mid-1; } } return ans; } int main() { ll n,m,x,y,i; char pd,d; cin>>(s+1)>>m; n=strlen(s+1); for(i=0;i<=200000;i++) { jc[i]=(i==0)?1:(jc[i-1]*base); } for(i=1;i<=n;i++) { T.insert(i-1,s[i]); } for(i=1;i<=m;i++) { cin>>pd; if(pd=='Q') { cin>>x>>y; cout<<query_lcp(n,x,y)<<endl; } if(pd=='R') { cin>>x>>d; T.update(x,d); } if(pd=='I') { cin>>x>>d; n++; T.insert(x,d); } } return 0; }
5.20
闲话
- 详见 2024 HE中考 游记 5.20 。
- 晚三现班主任讲要对奥赛培养兴趣时,称 @K8He 和 @jijidawang 学奥赛学得 \(whk\) 都不想上了,我们这些留在班里的看着心也有点痒痒;然后设想要是去年暑假或寒假前就把我们选出来了能多学多少东西。
做题纪要
本文来自博客园,作者:hzoi_Shadow,原文链接:https://www.cnblogs.com/The-Shadow-Dragon/p/18185039,未经允许严禁转载。
版权声明:本作品采用 「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0) 进行许可。

 ,取
,取  或
或  ,图来自
,图来自  ,取
,取  或
或  ,图来自
,图来自 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号