初三奥赛模拟测试2

\(T1\) 南 \(0pts\)

原题： luogu P4550 收集邮票
设 \(f_{i}\) 表示当前已经买了 \(i\) 种武器，要买完 \(n\) 种武器的期望次数，有 \(\begin{cases} f_{i}=0 & i=n \\ f_{i}= \frac{i}{n} \times (f_{i}+1)+ \frac{n-i}{n} \times (f_{i+1}+1) & i \ne n \end{cases}\) ，移项得 \(\begin{cases} f_{i}=0 & i=n \\ f_{i}=f_{i+1}+ \frac{n}{n-i} & i \ne n \end{cases}\) 。
- 这部分同 SP1026 FAVDICE - Favorite Dice 。
设 \(g_{i}\) 表示当前已经买了 \(i\) 种武器，要买完 \(n\) 种武器的期望钱数，有 \(\begin{cases} g_{i}=0 & i=n \\ g_{i}= \frac{i}{n} \times (f_{i}+1+g_{i})+ \frac{n-i}{n} \times (f_{i+1}+1+g_{i+1}) & i \ne n \end{cases}\) ，移项得 \(\begin{cases} g_{i}=0 & i=n \\ g_{i}= \frac{i}{n-i} \times f_{i}+f_{i+1}+g_{i+1}+ \frac{n}{n-i} & i \ne n \end{cases}\) 。
点击查看代码
```
double f[10010],g[10000];
int main()
{
	int n,i;
	cin>>n;
	f[n]=g[n]=0;
	for(i=n-1;i>=0;i--)
	{
		f[i]=f[i+1]+1.0*n/(n-i);
		g[i]=1.0*i/(n-i)*f[i]+f[i+1]+g[i+1]+1.0*n/(n-i);
	}
	printf("%.2lf\n",g[0]);
	return 0;
}
```

\(T2\) 昌 \(0pts\)

原题： CF1153D Serval and Rooted Tree
部分分
- \(20pts\) ：生成 \(1 \sim k\) 的所有全排列依次填给叶节点，枚举每种情况即可。
正解
- 设 \(g_{x}\) 表示第 \(x\) 个节点的权值，容易发现 \(\begin{cases} (\sum\limits_{y \in Son(x)}[g_{y} \ge g_{x}]) \ge 1 & a_{x}=1 \\ (\sum\limits_{y \in Son(x)}[g_{y} \ge g_{x}])=dout_{x} & a_{x}=0 \end{cases}\) ，即当 \(a_{x}=0\) 时，其所有子节点的权值都会影响该节点的值；当 \(a_{x}=1\) 时，可选择任意一个满足 \(g_{y} \ge g_{x}\) 的子节点来影响该节点的值。
- 设 \(f_{x}\) 表示最少有多少个叶节点会影响第 \(x\) 个节点的值，状态转移方程为 \(f_{x}= \begin{cases} 1 & dout_{x}=0 \\ \min\limits_{y \in Son(x)} \{ f_{y} \} & dout_{x} \ne 0,a_{x}=1 \\ \sum\limits_{y \in Son(x)}f_{y} & dout_{x} \ne 0,a_{x}=0 \end{cases}\) 。
- 对于影响第 \(1\) 个节点的 \(f_{1}\) 个叶节点，选择 \((k-f_{1}+1) \sim k\) 将其填入即可；又因为这 \(f_{1}\) 个节点的权值必须 \(\ge g_{1}\) ，故有 \(\max \{ g_{1} \}=k-f_{1}+1\) 。
  点击查看代码
```
struct node
{
	int nxt,to;
}e[600010];
int head[600010],a[600010],f[600010],dout[600010],cnt=0;
void add(int u,int v)
{
	cnt++;
	e[cnt].nxt=head[u];
	e[cnt].to=v;
	head[u]=cnt;
}
void dfs(int x)
{   
	f[x]=(dout[x]==0)?1:(a[x]==1?0x7f7f7f7f:0);
	for(int i=head[x];i!=0;i=e[i].nxt)
	{
		dfs(e[i].to);
		f[x]=(a[x]==1)?min(f[x],f[e[i].to]):f[x]+f[e[i].to];    
	}
}
int main()
{
	int n,k=0,u,v,i;
	cin>>n;
	for(i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(i=2;i<=n;i++)
	{
		cin>>u;
		v=i;
		add(u,v);
		dout[u]++;
	}
	for(i=1;i<=n;i++)
	{
		k+=(dout[i]==0);
	}
	dfs(1);
	cout<<k-f[1]+1<<endl;
	return 0;
}
```

\(T3\) 起 \(0pts\)

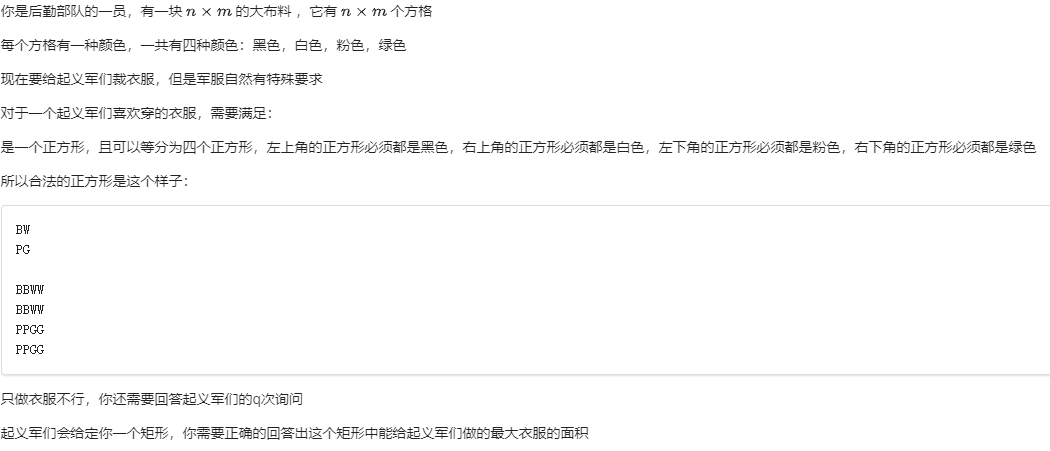
部分分
- \(Subtasks1(1pts)\)
  - 由于 \(n=1\) ，故不存在合法的衣服。
  - 对于每组询问输出 0 即可。

正解

设 \(g_{i,j,k}\) 表示以 \((i,j)\) 为右下角的颜色为 \(k\) 的正方形的最长长度，状态转移方程为 \(g_{i,j,k}= \min(g_{i-1,j,k},g_{i,j-1,k},g_{i-1,j-1,k})+1\) 。
- 状态转移方程比较常见，比如 luogu P1387 最大正方形， luogu P2701 [USACO5.3] 巨大的牛棚Big Barn 和 luogu P2280 [HNOI2003] 激光炸弹。
设 \(f_{i,j,k}\) 表示是否存在以 \((i,j)\) 为右下角的颜色为 \(k\) 的合法的正方形，状态转移方程为 \(f_{i+2k-1,j+2k-1,k}=[f_{i+k-1,j+k-1,j} \ge k \And\And f_{i+k-1,j+2k-1,j}=k \And\And f_{i+2k-1,j+k-1,j}=k \And\And f_{i+2k-1,j+2k-1,j}=k]\) 。
然后预处理出 \(f\) 的二维前缀和 \(sum\) 。

询问时考虑二分答案，对边长的一半进行二分，然后进行判定即可。

点击查看代码

int g[510][510][5],f[510][510][260],sum[510][510][260];
int val(char x)
{
	if(x=='B')
	{
		return 1;
	}
	if(x=='W')
	{
		return 2;
	}
	if(x=='P')
	{
		return 3;
	}
	if(x=='G')
	{
		return 4;
	}
	return 0;
}
bool check(int mid,int x1,int y1,int x2,int y2)
{
	return sum[x2][y2][mid]+sum[x1-1][y1-1][mid]-sum[x2][y1-1][mid]-sum[x1-1][y2][mid]>0;
}
int main()
{
	int n,m,q,x1,y1,x2,y2,l,r,ans,mid,i,j,k;
	char pd;
	scanf("%d%d%d",&n,&m,&q);
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)
		{
			cin>>pd;
			g[i][j][val(pd)]=min(g[i-1][j][val(pd)],min(g[i][j-1][val(pd)],g[i-1][j-1][val(pd)]))+1;
		}
	}
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)
		{
			for(k=1;i+2*k-1<=n&&j+2*k-1<=m;k++)
			{
				f[i+2*k-1][j+2*k-1][k]=(g[i+k-1][j+k-1][1]>=k&&g[i+k-1][j+2*k-1][2]==k&&g[i+2*k-1][j+k-1][3]==k&&g[i+2*k-1][j+2*k-1][4]==k);
			}
		}
	}
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)
		{
			for(k=1;k<=min(n,m)/2;k++)
			{
				sum[i][j][k]=sum[i-1][j][k]+sum[i][j-1][k]-sum[i-1][j-1][k]+f[i][j][k];
			}
		}
	}
	for(i=1;i<=q;i++)
	{
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		ans=0;
		l=1;
		r=min(x2-x1+1,y2-y1+1)/2;
		while(l<=r)
		{
			mid=(l+r)/2;
			if(check(mid,x1+2*mid-1,y1+2*mid-1,x2,y2)==true)
			{
				ans=mid;
				l=mid+1;
			}
			else
			{
				r=mid-1;
			}
		}
		printf("%d\n",ans*2*ans*2);
	}
	return 0;
}

\(T4\) 义 \(0pts\)

原题： LibreOJ 6089. 小 Y 的背包计数问题

部分分

\(30pts\) ：多重背包统计方案数。

点击查看代码

const ll p=23333333;
ll w[100010],c[100010],f[100010];
int main()
{
	ll n,i,j,k;
	cin>>n;
	for(i=1;i<=n;i++)
	{
		w[i]=c[i]=i;
	}
	f[0]=1;
	for(i=1;i<=n;i++)
	{
		for(k=n;k>=0;k--)
		{
			for(j=1;j<=c[i]&&j*w[i]<=k;j++)
			{
				f[k]=(f[k]+f[k-j*w[i]])%p;
			}
		}
	}
	cout<<f[n]<<endl;
	return 0;
}

正解
- 感觉和 BZOJ3462 DZY Loves Math II 挺像。
- 观察到前 \(\sqrt{n}\) 种物品存在被取完的可能，而 \(\sqrt{n}+1 \sim n\) 种物品不可能被取完。
- 设 \(f_{i,j}\) 表示当前已经取完了第 \(i\) 种物品，此时背包容量为 \(j\) 的方案数，状态转移方程为 \(f_{i,j}=f_{i,j-i}+f_{i-1,j}-f_{i-1,j-i(i+1)}\) 。
  - 因为第 \(i\) 种物品只能选 \(i\) 次，所以要减去多加的。
  - 关于 \(-f_{i-1,j-i(i+1)}\) 的理性理解可参考 NOIP模拟测试A2 D.义。
- 设 \(g_{i,j}\) 表示 \(\sqrt{n}+1 \sim n\) 种物品中已经取了 \(i\) 件，此时背包容量为 \(j\) 的方案数，状态转移方程为 \(g_{i,j}=g_{i,j-i}+g_{i-1,j-\sqrt{n}-1}\) 。
  - \(+g_{i,j-i}\) 表示取了的 \(i\) 件物品的价值均减 \(1\) 。
  - \(+g_{i-1,j-\sqrt{n}-1}\) 表示取了第 \(\sqrt{n}+1\) 件物品。
- 需要滚动数组优化 \(f\) 。
  点击查看代码
```
const ll p=23333333;
ll f[320][100010],g[320][100010];
int main()
{
	ll n,ans=0,N,i,j;
	cin>>n;
	N=sqrt(n);
	f[0][0]=f[1][0]=g[0][0]=1;
	for(i=1;i<=N;i++)
	{
		for(j=1;j<=n;j++)
		{
			f[i&1][j]=f[(i-1)&1][j];
			if(j-i>=0)
			{
				f[i&1][j]=(f[i&1][j]+f[i&1][j-i])%p;
			}
			if(j-i*(i+1)>=0)
			{
				f[i&1][j]=(f[i&1][j]-f[(i-1)&1][j-i*(i+1)]+p)%p;
			}
		}
	}
	for(i=1;i<=N;i++)
	{
		for(j=i;j<=n;j++)
		{
			g[i][j]=g[i][j-i];
			if(j-N-1>=0)
			{
				g[i][j]=(g[i][j]+g[i-1][j-N-1])%p;
			}
		}
	}
	for(i=0;i<=n;i++)
	{
		for(j=0;j<=N;j++)
		{
			ans=(ans+f[N&1][i]*g[j][n-i]%p)%p;
		}
	}
	cout<<ans<<endl;
	return 0;
}
```

总结

\(T2\)
- 把 \(i\) 看出了 \(1\) ，导致我以为这题还需要构造整棵树。
- 我在 \(2023.6.13\) 的时候写了，但考这场的时候我一点也想不起来自己做过这题；整场模拟赛的题目名称也都看了，但也是一点也想不起来看过这场模拟赛。
\(T3\)
- 以为选择的衣服只有左上角一个正方形必须是黑色，其他颜色同理。

后记

整活内容
- 更多信息详见八一特别行动社论。
\(T4\) 题解有个地方写错了，但 \(miaomiao\) 没给我们说要改。

posted @ 2024-03-15 17:48 hzoi_Shadow 阅读(44) 评论(1) 编辑收藏举报

刷新页面返回顶部

hzoi_Shadow

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。纵使世界万般残酷，总有温暖值得守护……

初三奥赛模拟测试2

初三奥赛模拟测试2

\(T1\) 南 \(0pts\)

\(T2\) 昌 \(0pts\)

\(T3\) 起 \(0pts\)

\(T4\) 义 \(0pts\)

总结

后记

公告

hzoi_Shadow

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。 纵使世界万般残酷，总有温暖值得守护……

初三奥赛模拟测试2

初三奥赛模拟测试2

\(T1\) 南 \(0pts\)

\(T2\) 昌 \(0pts\)

\(T3\) 起 \(0pts\)

\(T4\) 义 \(0pts\)

总结

后记

公告

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。纵使世界万般残酷，总有温暖值得守护……