UVA1108 Mining Your Own Business 题解

题目传送门

题意

在一个无向图上选择尽量少的点涂黑，使得删除任意一个点后，每个连通分量里都至少有一个黑点（多组数据）。

正文

观察题意，发现这是个 Tarjan 求点双连通分量的板子。

考虑在求点双连通分量的时候把割点顺便求出来，令第 \(i\) 个点双连通分量的大小为 \(size_i\)，然后进行分类讨论：

• 当第 \(i\) 个点双连通分量中没有割点时，符合题意则需要涂黑两个点，方案总数增加 \(C_{size_i}^2=\frac{size_i!}{{(size_i-2)}!×2!}=\frac{size_i(size_i-1)}{2}\)。

  • 如图，\((1,2,3,4)\) 为本图的点双连通分量，且没有割点，则在 \((1,2,3,4)\) 中任选两个点涂黑。

  

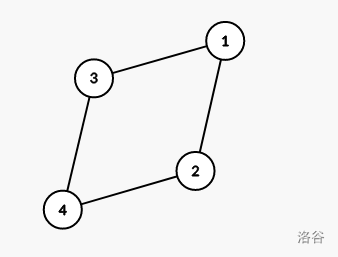
• 当第 \(i\) 个点双连通分量中有 \(1\) 个割点时，若符合题意则需要涂黑一个点（不能将割点涂黑），方案总数增加 \(C_{size_i-1}^1=\frac{(size_i-1)!}{{(size_i-2)}!×1!}=size_i-1\)。

  • 如图，\((1,2,6,3,5),(1,4)\) 为本图的两个点双连通分量，且 \(1\) 为本图的割点，则在 \((2,6,3,5),(4)\) 中各任选出一个点涂黑。

  

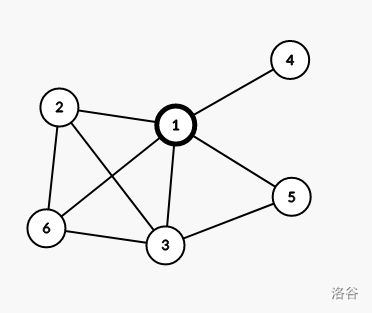
• 当第 \(i\) 个点双连通分量中的割点个数大于 \(1\) 时，不需要涂黑。

  • 如图，点双连通分量 \((2,5,6)\) 中有两个割点，则不需要涂黑。

  

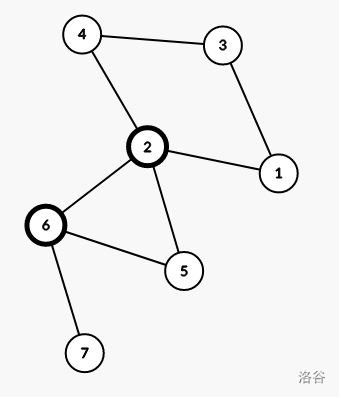
  • 证明：当割点删除后，可以通过另一个割点达到其他点双连通分量。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define sort stable_sort 
#define endl '\n'
struct node
{
	ll next,to;
}e[400001];
vector<ll>v_dcc[400001];
stack<ll>s;
ll head[400001],dfn[400001],low[400001],cut[400001],cnt,tot,ans;
void add(ll u,ll v)
{
	cnt++;
	e[cnt].next=head[u];
	e[cnt].to=v;
	head[u]=cnt;
}
void tarjan(ll x,ll fa)
{
    ll i,k=0,son=0;
    tot++;
    dfn[x]=low[x]=tot;
    s.push(x);
    for(i=head[x];i!=0;i=e[i].next)
    {
        if(dfn[e[i].to]==0)
        {
            tarjan(e[i].to,fa);
            low[x]=min(low[x],low[e[i].to]);
            if(low[e[i].to]>=dfn[x])
            {
                son++;
                if(x!=fa||son>=2)//求割点
                {
                    cut[x]=1;
                }
                ans++;
                v_dcc[ans].clear();//初始化
                v_dcc[ans].push_back(x);
                while(e[i].to!=k)
                {
                    k=s.top();
                    v_dcc[ans].push_back(k);
                    s.pop();
                }                
            }
        }
        else
        {
           low[x]=min(low[x],dfn[e[i].to]);
        }
    }
}
int main()
{
	ll n,m,i,j,u,v,sum=0,num,len,ans1,ans2;
    while(cin>>m)
    {
        if(m==0)
        {
            break;
        }
        else
        {
            n=0;
            sum++;
            tot=ans=cnt=ans1=0;
            ans2=1;
            while(s.empty()==0)
            {
                s.pop();
            }
            memset(e,0,sizeof(e));//多测不清空，爆零两行泪
            memset(low,0,sizeof(low));
            memset(dfn,0,sizeof(dfn));
            memset(cut,0,sizeof(cut));
            memset(head,0,sizeof(head));
            for(i=1;i<=m;i++)
            {
                cin>>u>>v;
                n=max(n,max(u,v));//n的个数需要自己求
                add(u,v);
                add(v,u);
            }
            for(i=1;i<=n;i++)
            {
                if(dfn[i]==0)
                {
                    tarjan(i,i);
                }
            }
            for(i=1;i<=ans;i++)
            {
                num=0;
                len=v_dcc[i].size();
                for(j=0;j<len;j++)
                {
                    if(cut[v_dcc[i][j]]==1)//判断是否是割点
                    {
                        num++;
                    }
                }
                if(num==0)//如果没有割点
                {
                    ans1+=2;
                    ans2*=(len-1)*len/2;
                }
                if(num==1)//如果有一个割点
                {
                    ans1++;
                    ans2*=len-1;
                }
            }
            cout<<"Case "<<sum<<": "<<ans1<<" "<<ans2<<endl;
        }
    }
    return 0;
}

---

后记

三倍经验 luoguP3225 [HNOI2012] 矿场搭建 | SP16185 BUSINESS - Mining your own business | UVA1108 Mining Your Own Business