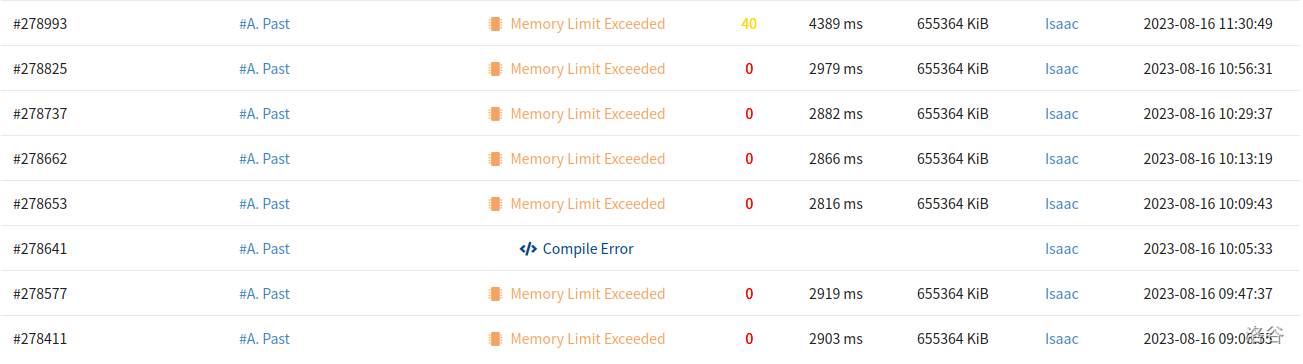
普及模拟1

合集 - 2023暑假集训(15)

1.2023年多校联训NOIP层测试12023-07-31 2.2023年多校联训NOIP层测试22023-08-02 3.2023年多校联训NOIP层测试3+「SFCOI-3」Sadness Fan Club Round 32023-08-05 4.2023年多校联训NOIP层测试4+洛谷 8 月月赛 I & RiOI Round 22023-08-05 5.【LGR-148-Div.3】洛谷基础赛 #1 & MGOI Round I2023-08-07 6.2023年多校联训NOIP层测试52023-08-07 7.2023年多校联训NOIP层测试62023-08-09 8.【LGR-154-Div.4】洛谷入门赛 #152023-08-13 9.2023年多校联训NOIP层测试7+【LGR-149-Div.3】洛谷基础赛 #2 & qw Round -12023-08-13

10.普及模拟12023-08-16

11.普及模拟2 +【LGR-155-Div.3】洛谷基础赛 #3 &「NnOI」Round 22023-08-19 12.普及模拟32023-11-17 13.【LGR-153-Div.2】梦熊联盟 8 月月赛 Ⅳ & Cfz Round 1 & 飞熊杯 #12023-08-26 14.【LGR-156-Div.3】洛谷网校 8 月普及组月赛 I & MXOI Round 1 & 飞熊杯 #2（同步赛）2023-08-27 15.2023暑假集训总结2023-08-26

普及模拟1

$T 1$ Past $0 p t s$

简化题意：已知一个长度为 $n (1 \leq n \leq 3 \times 10^{6})$ 的序列 $a$ ，给定一个 $d (0 \leq d \leq 3)$ ，有如下操作（所有操作对 $1336363663$ 取模）：
- 当 $1 \leq d$ 时，求 $\sum_{l = 1}^{n} \sum_{r = l}^{n} \sum_{k = l}^{r} a_{k}$ 。
- 当 $2 \leq d$ 时，求 $\sum_{l = 1}^{n} \sum_{r = l}^{n} ({max}_{k = l}^{r} {a_{k}} - {min}_{k = l}^{r} {a_{k}})$ 。
- 当 $3 \leq d$ 时，求 $n! \times \sum_{l = 1}^{n} \sum_{l e n = 1}^{n - l + 1} \frac{\sum_{k = l}^{l + l e n - 1} a_{k}}{l e n}$ 。
部分分：
- $O (n^{3})$ 暴力枚举： $T L E$ $50 p t s$
- $O (n^{2} + n \log_{2} (n))$
  - 线段树维护极差： $T L E$ $50 p t s$
  - $S T$ 表维护极差： $M L E + T L E$ $40 p t s$
    - $S T$ 表数组开太大了，全部 $M L E$ 挂了 $40 p t s$ 。
正解：
- $d = 1$
  - 打表发现第 $i$ 个数对答案产生的贡献为 $a_{i} \times i \times (n - i + 1)$ ，最后的答案即为 $\sum_{i = 1}^{n} a_{i} \times i \times (n - i + 1)$ 。
    - 证明：包含第 $i$ 个数的子序列的左端点一定在 $[1, i]$ 内，右端点一定在 $[i, n]$ 内。依据乘法原理，包含第 $i$ 个数的子区间一共有 $i \times (n - i + 1)$ 个，故第 $i$ 个数对答案产生的贡献为 $a_{i} \times i \times (n - i + 1)$ 。
- $d = 2$
  - 考虑将式子拆开，有 $\sum_{l = 1}^{n} \sum_{r = l}^{n} {max}_{k = l}^{r} {a_{k}} - {min}_{k = l}^{r} {a_{k}} = \sum_{l = 1}^{n} \sum_{r = l}^{n} {max}_{k = l}^{r} {a_{k}} - \sum_{l = 1}^{n} \sum_{r = l}^{n} {min}_{k = l}^{r} {a_{k}}$ 。令 $f_{i} = \sum_{l = 1}^{i} {max}_{k = l}^{i} {a_{k}}, g_{i} = \sum_{l = 1}^{i} {min}_{k = l}^{i} {a_{k}}$ ，即 $f_{i}$ 表示以 $i$ 结尾的所有子序列的最大值之和， $g_{i}$ 表示以 $i$ 结尾的所有子序列的最小值之和，最终答案即为 $\sum_{i = 1}^{n} (f_{i} - g_{i})$ 。在 $1 \sim i$ 中，找到一个 $p$ 使得 $a_{p} > a_{i}$ ，且 $p$ 最大（若不存在，则有 $p = 0$ ），那么就得到了状态转移方程 $f_{i} = f_{p} + a_{i} (i - p)$ ，将 $p$ 用单调栈进行维护，对于 $g$ 同理。
    - 原题：luogu P6503 [COCI2010-2011#3] DIFERENCIJA | SP10622 DIFERENC - DIFERENCIJA | CF817D Imbalanced Array
- $d = 3$
  - 预处理出阶乘数组 $m u l_{1}, m u l_{2}$ 和前缀和数组 $s u m$ ，使得对于每一个 $i (1 \leq i \leq n)$ 均满足 $m u l_{1, i} = \prod_{k = 1}^{i} a_{k}, m u l_{2, i} = \prod_{k = i}^{n} a_{k}, s u m_{i} = \sum_{k = 1}^{n} a_{k}$ ，接着将式子拆开， $n! \times \sum_{l = 1}^{n} \sum_{l e n = 1}^{n - l + 1} \frac{\sum_{k = l}^{l + l e n - 1} a_{k}}{l e n} = \sum_{l = 1}^{n} \sum_{l e n = 1}^{n - l + 1} (\frac{n!}{l e n} \times \sum_{k = l}^{l + l e n - 1} a_{k})$ ，这样就省去了对浮点数和除法的计算（便于取模）。打表，得到每个元素对这段子序列的答案贡献次数如下：
    - 观察发现，长度为 $l e n$ 的子序列对答案产生的贡献为长度为 $l e n - 1$ 的子序列对答案产生的贡献+ $s u m_{n - l e n + 1} - s u m_{l e n - 1}$ ，那么维护一个临时变量 $l s$ 存储当前对答案产生的贡献，然后乘上 $m u l_{1, i - 1}, m u l_{1, i + 1}$ 即可。即 $l s_{l e n} = l s_{l e n - 1} + s u m_{n - l e n + 1} - s u m_{l e n - 1}$ ，最终答案即为 $\sum_{l e n = 1}^{n} l s_{l e n} \times m u l_{1, l e n - 1} \times m u l_{2, l e n + 1}$ ，边界为 $l s_{0} = 0$ 。
本题卡负数取模，记得有减法运算时先加模数再取模，加法、乘法运算时先取模再运算再取模。

本程序取模较多，吸氧（开 $O 2$ ）才能过，时间复杂度为 $O (n)$ 。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define sort stable_sort 
#define endl '\n'
const ll p=1336363663;
ll a[3000001],f[3000001],g[3000001],mul1[3000001],mul2[3000001],sum[3000001];
stack<ll>maxx,minn;
int main()
{
    freopen("pst.in","r",stdin);
    freopen("pst.out","w",stdout);
    ll n,d,i,j,ans1=0,ans2=0,ans3=0,ls=0;
    scanf("%lld%lld",&n,&d);
    mul1[0]=mul2[n+1]=1;
    for(i=1,j=n;i<=n,j>=1;i++,j--)
    {
        scanf("%lld",&a[i]);
        sum[i]=(sum[i-1]%p+a[i]%p)%p;
        mul1[i]=((mul1[i-1]%p)*(i%p))%p;
        mul2[j]=((mul2[j+1]%p)*(j%p))%p;
    }
    if(d>=1)
    {
        for(i=1;i<=n;i++)
        {
            ans1=(ans1+(((((a[i]%p)*(i%p))%p)%p)*((n-i+1)%p)%p))%p;
            while(maxx.empty()==0&&a[maxx.top()]<=a[i])
            {
                maxx.pop();
            }
            while(minn.empty()==0&&a[minn.top()]>=a[i])
            {
                minn.pop();
            }
            if(maxx.empty()==0)
            {
                f[i]=(f[maxx.top()]%p+(a[i]%p)*((i-maxx.top())%p))%p;
            }
            else
            {
                f[i]=(f[0]%p+(a[i]%p)*(i%p)%p)%p;
            }
            if(minn.empty()==0)
            {
                g[i]=(g[minn.top()]%p+(a[i]%p)*((i-minn.top())%p))%p;
            }
            else
            {
                g[i]=(g[0]%p+(a[i]%p)*(i%p)%p)%p;
            }
            maxx.push(i);
            minn.push(i);
            ls=(ls+sum[n-i+1]%p-sum[i-1]%p+p)%p;
            ans3=(ans3+((ls*(mul1[i-1]%p))%p*(mul2[i+1]%p))%p)%p;
        }
        for(i=1;i<=n;i++)
        {
            ans2=(ans2+(f[i]-g[i]+p)%p)%p;
        }
        printf("%lld\n",ans1);
        if(d>=2)
        {
            printf("%lld\n",ans2);
            if(d>=3)
            {
                printf("%lld\n",ans3);
            }
        }
    }
    return 0;
}

$T 2$ Present $100 p t s$

简化题意：对一个序列，进行两端插入，两端读取，两端删除，反转的操作。

luogu B3656 【模板】双端队列 1 变形，用数组模拟或 $d e q u e$ 维护数列，考虑开一个 $b o o l$ 类型的 $f l a g$ 记录是否进行颠倒。

每次颠倒时，将 $f l a g$ 取反即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define sort stable_sort 
#define endl '\n'
deque<ll>q;
int main()
{
    freopen("prs.in","r",stdin);
    freopen("prs.out","w",stdout);
    ll n,id,pd,x,i;
    bool flag=false;
    scanf("%lld%lld",&n,&id);
    for(i=1;i<=n;i++)
    {
        scanf("%lld",&pd);
        if(pd==0)
        {
            scanf("%lld",&x);
            if(flag==false)
            {
                q.push_front(x);
            }
            else
            {
                q.push_back(x);
            }
        }
        if(pd==1)
        {
            if(q.empty()==0)
            {
                if(flag==false)
                {
                    printf("%lld\n",q.front());
                    q.pop_front();
                }
                else
                {
                    printf("%lld\n",q.back());
                    q.pop_back();
                }
            }
            else
            {
                printf("0\n");
            }
        }
        if(pd==2)
        {
            scanf("%lld",&x);
            if(flag==false)
            {
                q.push_back(x);
            }
            else
            {
                q.push_front(x);
            }
        }
        if(pd==3)
        {
            if(q.empty()==0)
            {
                if(flag==false)
                {
                    printf("%lld\n",q.back());
                    q.pop_back();
                }
                else
                {
                    printf("%lld\n",q.front());
                    q.pop_front();
                }
            }
            else
            {
                printf("0\n");
            }
        }
        if(pd==4)
        {
            flag=(!flag);
        }
    }
    return 0;
}

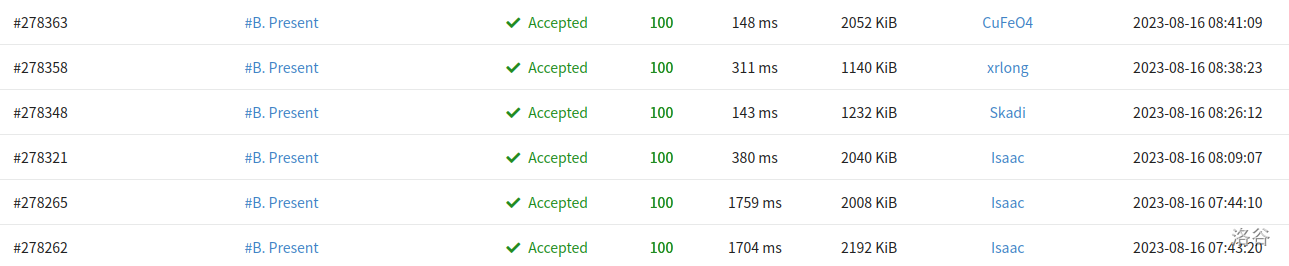
貌似是首A。

$T 3$ Future $100 p t s$

简化题意：给定一棵 $n$ 个节点的树，问从根节点（编号为 $1$ 的节点）到叶子结点的最大距离。
类似 luogu P1807 最长路，但本题是一棵树，跑树形 $D P$ ， $S P F A$ ，拓扑优化 $D P$ 求最长路等做法皆可。
- 树形 $D P$ 的一种做法，令 $f a_{i} (1 \leq i \leq n)$ 表示 $i$ 的父节点， $f_{i} (1 \leq i \leq n)$ 表示以 $i$ 为终点时，所得到的收获值，则有状态转移方程 $f_{i} = f_{f a_{i}} + w_{i}$ 。

坑：点权有负数，输出结果应初始化为 $- \infty$ 。

最后 $40 m i n$ 检查时才发现，差点挂了 $10 p t s$ 。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define sort stable_sort 
#define endl '\n'
struct node
{
    ll nxt,to;
}e[400001];
ll w[400001],f[400001],head[400001],dout[400001],cnt=0;//注意与上文数组定义不同
void add(ll u,ll v)
{
    cnt++;
    e[cnt].nxt=head[u];
    e[cnt].to=v;
    head[u]=cnt;
}
void dfs(ll x,ll fa)
{
    f[x]=f[fa]+w[x];
    for(ll i=head[x];i!=0;i=e[i].nxt)
    {
        if(e[i].to!=fa)
        {
            dfs(e[i].to,x);
        }
    }
}
int main()
{
    freopen("ftr.in","r",stdin);
    freopen("ftr.out","w",stdout);
    ll n,i,u,ans=-0x7f7f7f7f;
    scanf("%lld",&n);
    for(i=1;i<=n;i++)
    {
        scanf("%lld",&w[i]);
    }
    for(i=1;i<=n;i++)
    {
        scanf("%lld",&u);
        add(u,i);
        dout[u]++;//统计出度，为了找到终点
    }
    dfs(1,0);
    for(i=1;i<=n;i++)
    {
        if(dout[i]==0)
        {
            ans=max(ans,f[i]);
        }
    }
    printf("%lld\n",ans);
    return 0;
}

$T 4$ Beyond $0 p t s$

简化题意：给定一个 $n \times n (2 \leq n \leq 20)$ 大小的矩阵和常数 $f a t e$ ，记 $p a s t$ 为从 $(1, 1)$ 到对角线（即直线 $y = n - x + 1$ 上）的路径上每个方格的异或和， $f u t u r e$ 为从对角线走到 $(n, n)$ 的路径上每个方格的异或和。求 $p a s t + f a t e = f u t u r e$ 的方案数。
强化版：CF1006F Xor-Paths | [ABC271F] XOR on Grid Path
部分分：
- $10 p t s$ ：输出 0 。

正解：考虑爆搜(明显的暗示，其实是

m e e t i n m i d d l e

)，分别从

(1, 1), (n, n)

进行爆搜，当到达对角线时，将所得到的值分别用两个

m a p

进行存储，又因为在对角线可以进行传送至另一个对角线，然后利用加法原理和乘法原理求解。

对于每个 $p a s t$ 在 $f u t u r e$ 中用 $m a p$ 的 $. f i n d ()$ 或其他方式寻找 $p a s t + f a t e$ 出现的次数，即可进行求解。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define sort stable_sort 
#define endl '\n'
ll c[21][21],f[21][21],dil[2][2]={{1,0},{0,1}},dir[2][2]={{-1,0},{0,-1}};
map<ll,ll>l,r;
map<ll,ll>::iterator it,val;
void dfs1(ll x,ll y,ll n,ll num)
{
    if(y==n-x+1)
    {
        l[num]++;
    }
    else
    {
        ll i,nx,ny;
        for(ll i=0;i<=1;i++)
        {
            nx=x+dil[i][0];
            ny=y+dil[i][1];
            if(1<=nx&&nx<=n&&1<=ny&&ny<=n)
            {
                dfs1(nx,ny,n,num^c[nx][ny]);
            }
            
        }
    }
}
void dfs2(ll x,ll y,ll n,ll num)
{
    if(y==n-x+1)
    {
        r[num]++;
    }
    else
    {
        ll i,nx,ny;
        for(ll i=0;i<=1;i++)
        {
            nx=x+dir[i][0];
            ny=y+dir[i][1];
            if(1<=nx&&nx<=n&&1<=ny&&ny<=n)
            {
                dfs2(nx,ny,n,num^c[nx][ny]);
            }
        }
    }
}
int main()
{
    freopen("byd.in","r",stdin);
    freopen("byd.out","w",stdout);
    ll n,fate,i,j,ans=0,sum;
    scanf("%lld%lld",&n,&fate);
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        {
            scanf("%lld",&c[i][j]);
        }
    }
    dfs1(1,1,n,0);
    dfs2(n,n,n,0);
    for(it=l.begin();it!=l.end();it++)
    {
        val=r.find(it->first+fate);
        if(val!=r.end())
        {
            ans+=(it->second)*(val->second);//将两个数出现的次数相乘
        }
    }
    printf("%lld\n",ans);
    return 0;
}

总结

十年 $O I$ 一场空，不开 $l o n g l o n g$ 见祖宗。
本次开题顺序： $(T 2, T 3, T 1, T 4)$ ，在这里没有掉进出题人的坑里。
$T 4$ 没有再认真想想，如果想到爆搜的话可能分数再高点（？）。
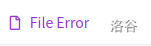
注意文件输入输出（有人在这里爆零了）。

后记

posted @ 2023-08-16 17:17 hzoi_Shadow 阅读(144) 评论(11) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 普及模拟3

· 欢欢乐乐赛赛

· 2023.8.16 普及模拟1

· 25/1/18 模拟赛做题记录

· ARC111F Do you like query problems? 题解

公告

昵称： hzoi_Shadow
园龄： 1年9个月
粉丝： 100
关注： 181

+加关注

2025年3月

日

一

二

三

四

五

六

随笔分类 (336)

随笔档案 (336)

文章档案 (1)

2025年2月(1)

hzoi_Shadow

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。纵使世界万般残酷，总有温暖值得守护……

普及模拟1

普及模拟1

$T 1$ Past $0 p t s$

$T 2$ Present $100 p t s$

$T 3$ Future $100 p t s$

$T 4$ Beyond $0 p t s$

总结

后记

公告

搜索

常用链接

最新随笔

我的标签

积分与排名

合集 (25)

随笔分类 (336)

随笔档案 (336)

文章档案 (1)

阅读排行榜

评论排行榜

推荐排行榜

最新评论

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。 纵使世界万般残酷，总有温暖值得守护……

T1 Past 0pts

T2 Present 100pts

T3 Future 100pts

T4 Beyond 0pts

总结

后记

公告

搜索

常用链接

最新随笔

积分与排名

合集 (25)

随笔分类 (336)

随笔档案 (336)

文章档案 (1)

世上只有一种英雄主义，就是认清生活的真相后，依然热爱生活。纵使世界万般残酷，总有温暖值得守护……

$T 1$ Past $0 p t s$

$T 2$ Present $100 p t s$

$T 3$ Future $100 p t s$

$T 4$ Beyond $0 p t s$