【学习笔记】Tarjan
更好的阅读体验
前言
凡事都得靠自己 --bobo
- 催隔壁 @K8He n 天了让他写 \(Tarjan\) 的学习笔记,但貌似还没有动静,所以决定自己写一个。
正文
- 本文配套题单:14.图论-tarjan(强连通分量、割点、割边)
前置知识
- 熟练使用链式前向星
- 在一张连通图中,所有的节点以及发生递归的边共同构成一棵搜索树。如果这张图不连通,则构成搜索森林。
- 如图(
从学校课件上扒下来的图)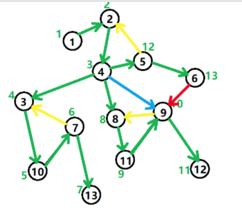
- \({\color{green}树边}\): \(DFS\) 时经过的点,即 \(DFS\) 搜索树上的边。
- \({\color{yellow}返祖边}\):也叫回边,与 \(DFS\) 方向相反,从某个节点指向其某个祖先的边。
- \({\color{red}横叉边}\): 从某个节点指向搜索树中另一子树终端某节点的边,它主要是在搜索的时候遇到了一个已经访问过的节点,但是这个节点并不是当前节点的祖先时形成的。
- 无向图不存在横叉边。
- \({\color{blue}前向边}\): 指向子树中节点的边,父节点指向子孙节点。
- PS:前向边无用,因为通过树边就能直接到达这个点。
- 返祖边与树边必定构成环,横叉边可能与树边构成环。
- 时间戳、追溯值
- 时间戳 \(dfn\) :用来标记某个节点在进 \(DFS\) 时被访问的时间顺序(由小到大)。
- 追溯值 \(low\) :用来表示从当前节点 \(x\) 作为搜索树的根节点出发,能够访问到的所有节点中,时间戳 (\(dfn\))最小的值。
- 当 \(dfn[x]==low[x]\) 时,以 \(x\) 为根的搜索子树中所有节点是一个强连通(从栈顶到 \(x\) 的所有节点)分量。
- \(low[x]\) 的计算方法
- 如果 \(x->y\) 是树边(没有被访问过),那么 \(low[x]=min(low[x],low[y])\) 。
- 如果 \(x->y\) 是返祖边(访问过,且在栈中),那么 \(low[x]=min(low[x],dfn[y])\) 。
- 如果 \(x->y\) 是横叉边(不在栈中),那么什么都不做。
for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to); low[x]=min(low[x],low[e[i].to]); } else { if(ins[e[i].to]==1)//ins[x]表示x是否在栈内 { low[x]=min(low[x],dfn[e[i].to]); } } }
- 时间复杂度 \(\Theta(N+M)\)
- 运行 \(Tarjan\) 算法的过程中,每个节点都被访问了一次,且只进出了一次栈,每条边也只被访问了一次,故时间复杂度为 \(\Theta(N+M)\) 。
Tarjan 与有向图
强连通分量(Strongly Connected Components,SCC)
- 强连通(strongly connected):在一个有向图 \(G\) 里,设有两个点 \(a,b\) ,由 \(a\) 有一条路可以走到 \(b\) ,由 \(b\) 又有一条路可以走到 \(a\) ,则称这两个顶点 \((a,b)\) 强连通。
- 强连通图:如果在一个有向图 \(G\) 里,每两个点都强连通,则称 \(G\) 是一个强连通图。
- 强连通分量:非强连通图有向图的极大强连通子图,称为强连通分量(Strongly Connected Components,SCC)。
- 如果节点 \(x\) 是某个强连通分量在搜索树中遇到的第一个节点,那么这个强连通分量的其余节点肯定在搜索树中以 \(x\) 为根的子树中,节点 \(x\) 被称为这个强连通分量的根。
- 例题
-
luogu B3609 [图论与代数结构 701] 强连通分量
#include<bits/stdc++.h> using namespace std; #define ll long long #define endl '\n' struct node { int next,to; }e[100001]; vector<int>scc[100001]; stack<int>s; int head[100001],dfn[100001],low[100001],ins[100001],vis[100001],c[100001],cnt=0,tot=0,ans=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].to=v; head[u]=cnt; } void tarjan(int x) { int i,k=0; tot++; dfn[x]=low[x]=tot; ins[x]=1; s.push(x); for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to); low[x]=min(low[x],low[e[i].to]); } else { if(ins[e[i].to]==1)//说明e[i].to是祖先节点or左子树节点 { low[x]=min(low[x],dfn[e[i].to]); } } } if(dfn[x]==low[x])//如果这里构成了一个强连通分量 { ans++;//ans是强连通分量的编号 while(x!=k)//将这个强连通分量内的点标记一下 { k=s.top(); ins[k]=0; c[k]=ans;//c[k]表示k属于哪个强连通分量内 scc[ans].push_back(k); s.pop(); } } } int main() { int n,m,i,j,u,v; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; add(u,v); } for(i=1;i<=n;i++) { if(dfn[i]==0) { tarjan(i); } } cout<<ans<<endl; for(i=1;i<=n;i++) { if(vis[c[i]]==0) { vis[c[i]]=1; sort(scc[c[i]].begin(),scc[c[i]].end()); for(j=0;j<scc[c[i]].size();j++) { cout<<scc[c[i]][j]<<" "; } cout<<endl; } } return 0; } -
luogu P2661 [NOIP2015 提高组] 信息传递
- 易知本题答案为最小的强连通分量大小(非 \(1\) )
\(maxin\) 即为结果scc=0; while(x!=k) { k=s.top(); ins[k]=0; scc++; s.pop(); } if(scc!=1) { maxin=min(maxin,scc); }
- 易知本题答案为最小的强连通分量大小(非 \(1\) )
-
luogu P2863 [USACO06JAN] The Cow Prom S
- 按照题意打就行
-
luogu P2921 [USACO08DEC] Trick or Treat on the Farm G 先跑一遍 \(Tarjan\) (这是一个有 \(n\) 个点,\(n\) 条边的图,故只有 \(1\) 个强连通分量的大小不为 \(1\) ),然后分类讨论:
- 若节点 \(x\) 所在强连通分量的大小不为 \(1\) ,则答案为 \(x\) 所在强连通分量的大小。
- 若节点 \(x\) 所在强连通分量的大小为 \(1\) ,则答案为节点 \(x\) 到不为1的强连通分量的距离 \(+\) 这个强连通分量的大小。
- 至于怎么求距离,记忆化搜索是个好东西。
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' struct node { int next,to; }e[100001]; stack<int>s; int head[100001],dfn[100001],low[100001],ins[100001],scc[100001],c[100001],u[100001],v[100001],anss[100001],cnt=0,tot=0,ans=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].to=v; head[u]=cnt; } void tarjan(int x) { int i,k=0; tot++; dfn[x]=low[x]=tot; ins[x]=1; s.push(x); for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to); low[x]=min(low[x],low[e[i].to]); } else { if(ins[e[i].to]==1) { low[x]=min(low[x],dfn[e[i].to]); } } } if(dfn[x]==low[x]) { ans++; while(x!=k) { k=s.top(); ins[k]=0; c[k]=ans; scc[ans]++; s.pop(); } } } void search(int rt,int x,int sum) { if(anss[x]==0) { search(rt,v[x],sum+1); } else { anss[rt]=anss[x]+sum; return; } } int main() { int n,i,j,sum; cin>>n; for(i=1;i<=n;i++) { u[i]=i; cin>>v[i]; add(u[i],v[i]); } for(i=1;i<=n;i++) { if(dfn[i]==0) { tarjan(i); } } for(i=1;i<=n;i++) { if(u[i]==v[i])//给自环打个标记 { anss[i]=1; } else { if(scc[c[u[i]]]>=2) { anss[i]=scc[c[u[i]]]; } } } for(i=1;i<=n;i++) { if(anss[i]==0) { search(u[i],v[i],1); } } for(i=1;i<=n;i++) { cout<<anss[i]<<endl; } return 0; }
- 至于怎么求距离,记忆化搜索是个好东西。
-
缩点
- 缩点:把强连通分量看作一个大点,并保留不在此强连通分量内的边,重新建图(易知此时的图是一个 DAG ,可以进行拓扑排序)。
if(dfn[x]==low[x]) { ans++; while(x!=k) { k=s.top(); ins[k]=0; c[k]=ans; b[ans]+=a[k];//a[]为原点权,b[]为缩点后的点权 s.pop(); } }cnt=0; memset(e,0,sizeof(e)); memset(head,0,sizeof(head)); for(i=1;i<=m;i++) { if(c[u[i]]!=c[v[i]])//Pursuing_OIer 教给我的神奇的建边方法(其实很好理解) { add(c[u[i]],c[v[i]]); } } - 例题
- luogu P5145 漂浮的鸭子 跑一遍缩点,求最大环,把边权转换为点权即可。
- luogu P2002 消息扩散 ,luogu P2835 刻录光盘观察题意,易知结果为缩点后入度为 \(0\) 的点个数。
- luogu P2812 校园网络【[USACO]Network of Schools加强版】 第一问显然同luogu P2002,令 \(p,q\) 分别表示缩点后入度、出度为 \(0\) 的点的个数,第二问显然是要求 \(max(p,q)\) , 只有一个 \(SCC\) 时记得特判。
双倍经验luogu P2746 [USACO5.3] 校园网Network of Schools UVA12167 Proving Equivalences - luogu P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G 观察题意,易知缩点后若有强连通分量的个数 \(>1\) ,则无解;当只有 \(1\) 个强连通分量时,这个强连通分量的大小即为所求。
- luogu P2515 [HAOI2010] 软件安装 读完题,发现和luogu P2014 [CTSC1997] 选课 很像,只不过选课是一棵树,本题是一个图。可能本题建图有点麻烦,剩下的话,缩点后当树形 \(DP\) 做就行了。
for(i=1;i<=n;i++) { cin>>u[i]; v[i]=i; if(u[i]!=0) { add(u[i],v[i]); } } ······ cnt=0; memset(e,0,sizeof(e)); memset(head,0,sizeof(head)); for(i=1;i<=n;i++) { if(c[u[i]]!=c[v[i]]) { add(c[u[i]],c[v[i]]); din[c[v[i]]]++; } } for(i=1;i<=ans;i++) { if(din[i]==0) { add(0,i); } } - luogu P3387 【模板】缩点 缩点后跑最长路( \(SPFA\) or 拓扑)。
int top_sort() { queue<int>q; int i,k,num=0; for(i=1;i<=ans;i++) { if(din[i]==0) { q.push(i); dis[i]=b[i];//b[]为缩点后的点权 } } while(q.empty()==0) { k=q.front(); q.pop(); for(i=head[k];i!=0;i=e[i].next) { dis[e[i].to]=max(dis[e[i].to],dis[k]+b[e[i].to]); din[e[i].to]--; if(din[e[i].to]==0) { q.push(e[i].to); } } } for(i=1;i<=ans;i++) { num=max(num,dis[i]); } return num; }- 加强版->P3627 [APIO2009] 抢掠计划 增加了起点和终点限制(缩点时要进行存储),但总体改变不大,拓扑不太好打,所以就换 \(SPFA\) 了,代码 。
- 双倍经验:UVA11324 The Largest Clique
- CF999E Reachability from the Capital 读题,易知对于每个强连通分量缩点后入度为 \(0\) 的点的数量即为所求(起点所在强连通分量要特判),代码。
- luogu P3119 [USACO15JAN] Grass Cownoisseur G 读题,每个点原点权均为1(且一个点的点权只能算一次),题目要求分别以 \(1\) 为起点和终点(建反图就行了)的最长路,果断 \(SPFA\) ,但是这个缩点后建边不太好搞…………
- 因为分别以 \(1\) 为起点和终点(建反边就行了)的最长路会把 \(1\) 多算一次,记得减去 \(1\) 的点权。
- 结果初始值要设为 \(b[c[1]]\) ,因为可能没有边与 \(1\) 相连,比如
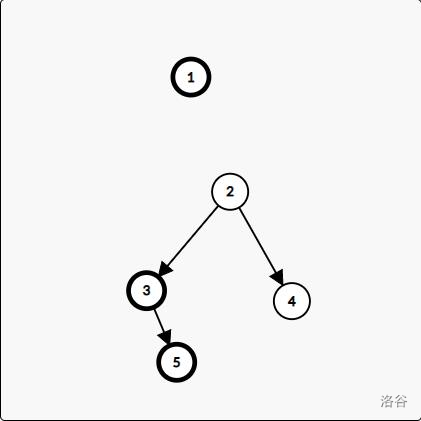
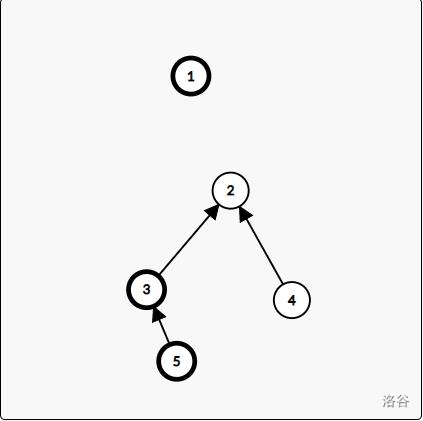 两张图分别对应原图和反图。
两张图分别对应原图和反图。 - 剩下的细节看代码吧。
- luogu P2321 [HNOI2006] 潘多拉的宝盒
- 简化题意:有 \(s\) 个咒语机,每个咒语机有 \(n\) 个元件,每个元件的出度为 \(2\) (字符串后面加 \(0\) 指向一个元件,字符串后面加 \(1\) 指向另一个元件),又有 \(m\) 个输出元。称从一个元件出发,以一个咒语机结尾而产生的字符串为一种方案。若咒语机 \(x\) 产生的所有方案包含咒语机 \(y\) 产生的所有方案,则称咒语机 \(x\) 是咒语机 \(y\) 的升级。求最长升级序列的长度。
- 本题难在建图,但建图后 \(Tarjan\) 缩点+记忆化搜索记录最长链即可。
- 若在搜索过程中,一个宝盒出现输出元,而另一个没有没有出现,此时一定有这两个宝盒间不存在包含关系,即不存在升级;否则建一条起点为i,终点为j的有向边。
- 代码
潘多拉(图片来源:奥奇传说)
- CF131D Subway
- 本题有些特殊,因为是无向图。
- 题解 懒得搬了。
Tarjan 与无向图
无向图与割点(割顶)、割边(桥)
- 在一个无向图中,不存在横叉边(因为边是双向的)。
- 一个无向图中,可能不止存在一个割点或一条割边。
- 割点(割顶):在一个无向图中,若删除节点 \(x\) 以及所有与 \(x\) 相关联的边之后,图将会被分成两个或者两个以上不相连的子图,那么称 \(x\) 为这个图的割点(割顶)。
- 判定法则:
当遍历到一个节点 \(x\) 时,这个点为割点的情况有两种:- 该节点为根节点且子节点的个数 \(>1\) (易知此时对于 \(x\) 的任意一个子节点 \(y\) 都有 \(dfn[x]<low[y]\) ),则删掉这个节点 \(x\) 后必将导致子节点不连通,即该节点 \(x\) 为图的一个割点。
- 该节点不为根节点,且存在一个子节点 \(y\) 使得 \(dfn[x]≤low[y]\)(子节点 \(y\) 可回溯到的最早节点不早于 \(x\) 点,即子节点 \(y\) 无法回到 \(x\) 的祖先节点) ,则删掉这个节点 \(x\) 后必将导致 \(x\) 的父节点与 \(x\) 的子节点不连通,即该节点 \(x\) 为图的一个割点。
- 若不存在一个子节点 \(y\) 使得 \(dfn[x]≤low[y]\),说明子节点 \(y\) 能绕行其他边到达比 \(x\) 更早访问的节点, \(x\) 就不是本图的割点,即环内的点割不掉。
- 应用:如图,节点 \((0,4,5,6,7,11)\) 为割点。

- 例题
- luogu P3388 【模板】割点(割顶)
#include<bits/stdc++.h> using namespace std; #define ll long long #define endl '\n' struct node { int next,to; }e[400001]; int head[400001],dfn[400001],low[400001],flag[400001],cnt=0,tot=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].to=v; head[u]=cnt; } void tarjan(int x,int fa) { int i,k=0,son=0;//son用于存子节点个数 tot++; dfn[x]=low[x]=tot; for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to,fa); low[x]=min(low[x],low[e[i].to]); if(low[e[i].to]>=dfn[x]) { son++; if(x!=fa||son>=2) { flag[x]=1; } } } else { low[x]=min(low[x],dfn[e[i].to]); } } } int main() { int n,m,i,u,v,sum=0; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; add(u,v); add(v,u); } for(i=1;i<=n;i++) { if(dfn[i]==0) { tarjan(i,i); } } for(i=1;i<=n;i++) { sum+=flag[i]; } cout<<sum<<endl; for(i=1;i<=n;i++) { if(flag[i]==1) { cout<<i<<" "; } } return 0; }双倍经验(输入格式有点ex)UVA315 Network - luogu P3469 [POI2008] BLO-Blockade
- 考虑分类讨论:
- 若节点 \(x\) 不是割点,则删去所有与 \(x\) 相连的边后,只有 \(x\) 与其他 \(n-1\) 个点不连通,其他 \(n-1\) 个点之间仍然是连通的,故此时答案为 \(2(n-1)\) 。
- PS:因为是有序点对,即 \((x,y)\) 和 \((y,x)\) 是不同的点对。
- 若节点 \(x\) 是割点,则删去所有与 \(x\) 相连的边后,图为分成若干个连通块,求出各个连通块的大小后,两两相乘再相加即为此时答案。
- 设在搜索树中,节点 \(x\) 的子节点集合中,有 \(t\) 个节点 \(s_{1},s_{2},s_{3},…,s_{t}\) 满足割点判定法则 \(dfn[x]≤low[s_{k}](1≤k≤t)\) 。则删去所有与 \(x\) 相连的边后,这个图至多分成 \(t+2\) 个连通块,每个连通块的节点构成情况如下:
- \(1\) 个由节点 \(x\) 自身单独构成的连通块。
- \(t\) 个由搜索树上以 \(s_{k}(1≤k≤t)\) 为根的子树的节点构成的连通块。
- \(1\) 个由除了上述节点之外的所有节点构成的连通块(可以没有)。eg:搜索树上 \(x\) 父亲节点方向的所有节点。
- 跑一遍 \(Tarjan\) 求出搜索树每个子树的大小。设 \(size[x]\) 用来表示以 \(x\) 为根的子树大小,故此时答案为 \(size[s_{1}]×(n-size[s_{1}])+size[s_{2}]×(n-size[s_{2}])+…+size[s_{t}]×(n-size[s_{t}])+1×(n-1)+(n-1- \sum\limits_{k=1}^{t} size[s_{k}] )×(1+ \sum\limits_{k=1}^{t} size[s_{k}] )\) 。
- 设在搜索树中,节点 \(x\) 的子节点集合中,有 \(t\) 个节点 \(s_{1},s_{2},s_{3},…,s_{t}\) 满足割点判定法则 \(dfn[x]≤low[s_{k}](1≤k≤t)\) 。则删去所有与 \(x\) 相连的边后,这个图至多分成 \(t+2\) 个连通块,每个连通块的节点构成情况如下:
- 若节点 \(x\) 不是割点,则删去所有与 \(x\) 相连的边后,只有 \(x\) 与其他 \(n-1\) 个点不连通,其他 \(n-1\) 个点之间仍然是连通的,故此时答案为 \(2(n-1)\) 。
- 剩下细节看代码吧。
双倍经验SP15577 STC10 - Blockade
- 考虑分类讨论:
- luogu P3388 【模板】割点(割顶)
- 判定法则:
- 割边(桥):在一个无向图中,若删除边 \(e\) 之后,图将会被分成两个不相连的子图,那么称 \(e\) 为这个图的割边(桥)。
- 判定法则:当遍历到一个节点 \(x\) 时,与其子节点 \(y\) 的这条边 \(e\) ,使得 \(dfn[x]<low[y]\) (从 \(y\) 出发,若不经过边 \(e\) ,则无法到达 \(x\) 或 更早访问的节点),则这条边 \(e\) 为图的一条割边。
- 若 \(low[y]≤dfn[x]\) ,则说明 \(y\) 能通过其他的边到达 \(x\) 或 更早访问的节点,即这条边 \(e\) 不是图的一条割边。
- 注意事项:
- 有重边的边一定不是割边。
- 边是无方向的,所以父亲与孩子之间节点的关系需要自己规定,防止误认为环。
- 两个割点之间的边不一定是割边;割边的两个端点不一定是割点,但至少有一个是割点(eg:有重边)。
- 例题
- luogu P1656 炸铁路 读题,易知结果为图中的割边。
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' struct node { int from,to; }e[2001]; vector<int>E[2001]; int dfn[2001],low[2001],flag[2001],cnt=0,tot=0; void add(int u,int v) { cnt++; e[cnt].from=min(u,v); e[cnt].to=max(u,v); } void tarjan(int x,int fa) { int i,k=0,pd=0;//pd用来记录遍历x的子节点时是否回到了fa tot++; dfn[x]=low[x]=tot; for(i=0;i<E[x].size();i++)//不要写成i<=E[x].size()-1 { if(dfn[E[x][i]]==0) { tarjan(E[x][i],x); low[x]=min(low[x],low[E[x][i]]); if(low[E[x][i]]>dfn[x]) { add(x,E[x][i]); } } else { if(E[x][i]==fa&&pd==0) { pd=1; } else//若pd==1,则将其当作计算儿子节点的方法来更新当前节点的值。 { low[x]=min(low[x],dfn[E[x][i]]); } } } } bool cmp(node a,node b) { if(a.from==b.from) { return a.to<b.to; } else { return a.from<b.from; } } int main() { int n,m,i,u,v; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; E[u].push_back(v); E[v].push_back(u); } for(i=1;i<=n;i++) { if(dfn[i]==0) { tarjan(i,i); } } sort(e+1,e+1+cnt,cmp); for(i=1;i<=cnt;i++) { cout<<e[i].from<<" "<<e[i].to<<endl; } return 0; }
- luogu P1656 炸铁路 读题,易知结果为图中的割边。
- 判定法则:当遍历到一个节点 \(x\) 时,与其子节点 \(y\) 的这条边 \(e\) ,使得 \(dfn[x]<low[y]\) (从 \(y\) 出发,若不经过边 \(e\) ,则无法到达 \(x\) 或 更早访问的节点),则这条边 \(e\) 为图的一条割边。
无向图与双连通分量
- 若一个无向连通图不存在割点,则称它为点双连通图。
- 若一个无向连通图不存在割边,则称它为边双连通图。
- 无向图中极大的点双连通子图叫点双连通分量( \(v-DCC\) )。
- 无向图中极大的边双连通子图叫边双连通分量( \(e-DCC\) )。
- eg:
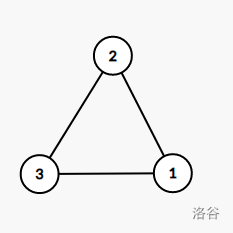
- eg:
- 点双连通分量和边双连通分量统称为双连通分量。
- 在一张连通的无向图中,对于两个点 \(x\) 和 \(y\) ,如果删去哪条边(只能删去一条)都不能使它们不连通,我们就说 \(x\) 和 \(y\) 边双连通。
- 在一张连通的无向图中,对于两个点 \(x\) 和 \(y\) ,如果删去哪个点(只能删去一个,且不能删去 \(x\) 和 \(y\) 自己)都不能使它们不连通,我们就说 \(x\) 和 \(y\) 点双连通。
点双连通分量
- 点双连通分量
- 若某个点为孤立点,则它自己单独构成一个 \(v-DCC\) 。
- 除了孤立点之外,点双连通分量的大小至少为 \(2\) 。
- 性质
- 点双连通分量之间以割点连接,且两个点双连通分量之间有且只有一个割点。
- 证明:若两个点双连通分量之间共用两个点,则删除其中任意一个点,所有点依旧连通。如图,
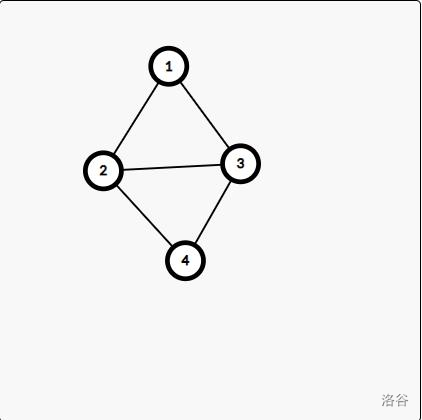
- 证明:若两个点双连通分量之间共用两个点,则删除其中任意一个点,所有点依旧连通。如图,
- 每一个割点可任意属于多个点双连通分量,因此求点双连通分量时,可能包含重复的点。
- 每一个割点都在至少两个点双连通分量中。
- 证明:在一个非点双连通图中,删去割点后图会不连通,故割点至少连接着图的两部分。但是因为点双连通图中不存在割点,所以这两部分肯定不在同一个点双连通分量中。因此割点至少存在于两个点双连通分量中。
- 只有一条边连通的两个点也是一个点双连通分量。如图
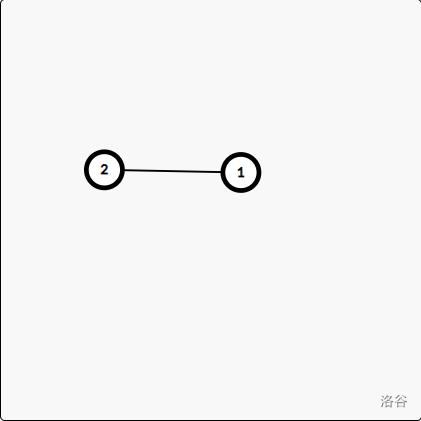
- 除了上一条中的情况外,其他的点双连通分量都满足任意两点间都存在不少于两条点不重复路径。
- 任意一个不是割点的点都只存在于一个点双连通分量中。
- 点双连通不具有传递性,如图,\((1,3)\) 点双连通,\((1,7)\) 点双连通,但是 \((3,7)\) 不点双连通。
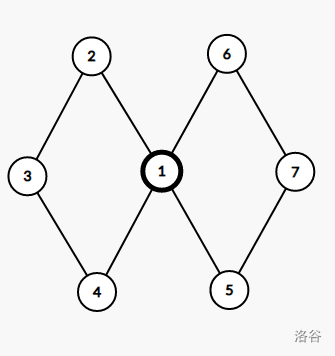
- 点双连通分量之间以割点连接,且两个点双连通分量之间有且只有一个割点。
- 应用:如图,存在( \(1,2,3\) ) , ( \(3,4\) ) , ( \(4,5,6\) ) 这三个点双连通分量。

- 算法
用一个栈存点,若遍历回到 \(x\) 时,发现割点判定法则 \(dfn[x]≤low[y]\) 成立,则从栈中弹出节点,直到 \(y\) 被弹出。那么,刚才弹出的节点和 \(x\) 一起构成一个 \(v-DCC\) 。
- 缩点
- 对每一个割点和 \(v-DCC\) 建点,然后根据从属关系连边,构成一棵树(或森林)。
- 例题
- luogu P8435 【模板】点双连通分量
- 事实上在求割点的同时,同时可以顺便求出点双连通分量,维护一个栈在求割点的途中若有 \(dfn[x]>low[y]\) ,则将 \((x,y)\) 入栈;而当 \(dfn[x]≤low[y]\) 时,将栈中所有在 \((x,y)\) 之上的边全部取出,这些边所连接的点与 \(x\) 构成了一个点双连通分量,显然割点是可以属于多个点双连通分量的。
- 每当新搜到一个节点时,将其压入栈中。
- 当发现 \(x\) 的子节点 \(y\) 不能通过其他方式到达 \(x\) 的祖先,但可以到达 \(x\)(即 \(dfn[x]≤low[y]\) 成立) ,则弹出栈顶元素直到 \(y\) 弹出。
- 弹出的所有元素组成的集合 \(E\) 加上 \(x\) ,则为一个点双连通分量。
#include<bits/stdc++.h> using namespace std; #define ll long long #define endl '\n' struct node { int next,to; }e[4000001]; vector<int>v_dcc[4000001]; stack<int>s; int head[4000001],dfn[4000001],low[4000001],cnt=0,tot=0,ans=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].to=v; head[u]=cnt; } void tarjan(int x,int fa) { int i,k=0; if(x==fa&&head[x]==0)//孤立点判定 { ans++; v_dcc[ans].push_back(x); } tot++; dfn[x]=low[x]=tot; s.push(x); for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to,fa); low[x]=min(low[x],low[e[i].to]); if(low[e[i].to]>=dfn[x]) { ans++; v_dcc[ans].push_back(x); while(e[i].to!=k)//弹栈时不能弹出割点,因为割点属于多个点双连通分量 { k=s.top(); v_dcc[ans].push_back(k); s.pop(); } } } else { low[x]=min(low[x],dfn[e[i].to]); } } } int main() { int n,m,i,j,u,v; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; if(u!=v)//重边会影响结果,记得特判 { add(u,v); add(v,u); } } for(i=1;i<=n;i++) { if(dfn[i]==0)//注意图可能不连通 { tarjan(i,i); } } cout<<ans<<endl; for(i=1;i<=ans;i++) { cout<<v_dcc[i].size()<<" "; for(j=0;j<v_dcc[i].size();j++) { cout<<v_dcc[i][j]<<" "; } cout<<endl; } return 0; } - luogu B3610 [图论与代数结构 801] 无向图的块
- 此题中的块即为大小不为 \(1\) 的点双连通分量,故不需要判断孤立点了。
- 再按字典序排序一下就行。
#include<bits/stdc++.h> using namespace std; #define ll long long #define endl '\n' struct node { int next,to; }e[4000001]; vector<int>v_dcc[4000001]; stack<int>s; int head[4000001],dfn[4000001],low[4000001],cnt=0,tot=0,ans=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].to=v; head[u]=cnt; } void tarjan(int x,int fa) { int i,k=0; tot++; dfn[x]=low[x]=tot; s.push(x); for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to,fa); low[x]=min(low[x],low[e[i].to]); if(low[e[i].to]>=dfn[x]) { ans++; v_dcc[ans].push_back(x); while(e[i].to!=k) { k=s.top(); v_dcc[ans].push_back(k); s.pop(); } } } else { low[x]=min(low[x],dfn[e[i].to]); } } } bool cmp(vector<int> x,vector<int> y) { for(int i=0;i<min(x.size(),y.size());i++) { if(x[i]!=y[i]) { return x[i]<y[i]; } } return x.size()<y.size(); } int main() { int n,m,i,j,u,v; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; if(u!=v) { add(u,v); add(v,u); } } for(i=1;i<=n;i++) { if(dfn[i]==0) { tarjan(i,i); } } cout<<ans<<endl; for(i=1;i<=ans;i++) { sort(v_dcc[i].begin(),v_dcc[i].end()); } sort(v_dcc+1,v_dcc+1+ans,cmp); for(i=1;i<=ans;i++) { for(j=0;j<v_dcc[i].size();j++) { cout<<v_dcc[i][j]<<" "; } cout<<endl; } return 0; } - luogu P3225 [HNOI2012] 矿场搭建
- 在求点双连通分量的时候把割点顺便求出来,令点双连通分量的大小为 \(size\) ,然后分类讨论:
- 当一个点双连通分量中没有割点时,需要建两个救援出口,方案总数增加 \(C_{size}^2=\frac{size!}{{(size-2)}!×2!}=\frac{size(size-1)}{2}\) 。如图,\((1,2,3,4)\) 为本图的点双连通分量,且没有割点,则在 \((1,2,3,4)\) 中任选两个点作为救援出口。
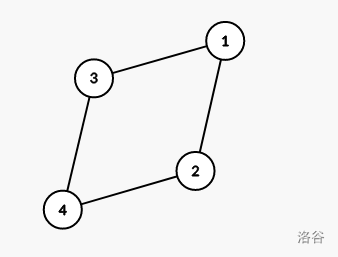
- 当一个点双连通分量中有 \(1\) 个割点时,需要建一个救援出口(不能建在割点上),方案总数增加 \(C_{size-1}^1=\frac{(size-1)!}{{(size-2)}!×1!}=size-1\) 。如图, \((1,2,6,3,5),(1,4)\) 为本图的两个点双连通分量,且 \(1\) 为本图的割点,则在 \((2,6,3,5),(4)\) 中各任选出一个点作为救援出口。
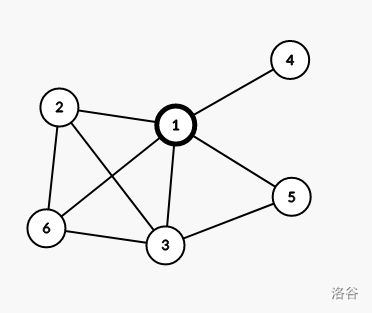
- 当一个点双连通分量中的割点个数大于 \(1\) ,不需要建救援出口。如图,点双连通分量 \((2,5,6)\) 中有两个割点,则不需要建救援出口。
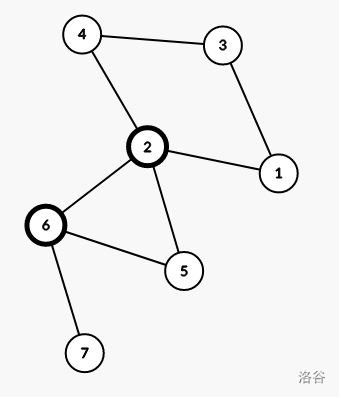
- 证明:当割点坍塌后,可以通过另一个割点达到其他点双连通分量。
- 当一个点双连通分量中没有割点时,需要建两个救援出口,方案总数增加 \(C_{size}^2=\frac{size!}{{(size-2)}!×2!}=\frac{size(size-1)}{2}\) 。如图,\((1,2,3,4)\) 为本图的点双连通分量,且没有割点,则在 \((1,2,3,4)\) 中任选两个点作为救援出口。
- 剩下的看代码吧。
三倍经验SP16185 BUSINESS - Mining your own business UVA1108 Mining Your Own Business
- 在求点双连通分量的时候把割点顺便求出来,令点双连通分量的大小为 \(size\) ,然后分类讨论:
- luogu P8435 【模板】点双连通分量
边双连通分量
- 边双连通分量
- 性质
- 边双连通具有传递性,即若 \(x,y\) 边双连通,\(y,z\) 边双连通,则 \(y,z\) 边双连通。如图,\((1,3)\) 边双连通,\((1,7)\) 边双连通,则 \((3,7)\) 边双连通。

- 边双连通具有传递性,即若 \(x,y\) 边双连通,\(y,z\) 边双连通,则 \(y,z\) 边双连通。如图,\((1,3)\) 边双连通,\((1,7)\) 边双连通,则 \((3,7)\) 边双连通。
- 算法
- 跑一遍 \(Tarjan\) 求出所有割边,然后把割边去掉,无向图会分成若干个连通块,每个连通块就是一个边双连通分量。
- 例题
- luogu P8436 【模板】边双连通分量
- \(DFS\) 写法
- 栈写法
#include<bits/stdc++.h> using namespace std; #define ll long long #define endl '\n' struct node { int next,to,flag; }e[4000001]; vector<int>e_dcc[4000001]; stack<int>s; int head[4000001],dfn[4000001],low[4000001],flag[4000001],dout[4000001],cnt=1,tot=0,ans=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].flag=0; e[cnt].to=v; head[u]=cnt; } void tarjan(int x,int fa) { int i,k=0; tot++; dfn[x]=low[x]=tot; s.push(x); for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to,i); low[x]=min(low[x],low[e[i].to]); if(low[e[i].to]>dfn[x])//割边判定法则 { e[i].flag=e[i^1].flag=1; } } else { if((fa^1)!=i) { low[x]=min(low[x],dfn[e[i].to]); } } } if(low[x]==dfn[x])//这里可以用DFS替代 { ans++; while(x!=k) { k=s.top(); s.pop(); e_dcc[ans].push_back(k); } } } int main() { int n,m,i,j,u,v; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; if(u!=v) { add(u,v); add(v,u); } } for(i=1;i<=n;i++) { if(dfn[i]==0) { tarjan(i,0); } } cout<<ans<<endl; for(i=1;i<=ans;i++) { cout<<e_dcc[i].size()<<" "; for(j=0;j<e_dcc[i].size();j++) { cout<<e_dcc[i][j]<<" "; } cout<<endl; } return 0; }
- luogu P8436 【模板】边双连通分量
- 性质
- 缩点
- 算法:把每一个边双连通分量缩成一个点使得原本的连通图变成一棵树(若原图不连通,则为树林),且树边就是原图的割边。其中满足 \(low[x]==dfn[x]\) 的节点 \(x\) ,这必定是一个边双连通分量的根。
- 证明:在一个边双连通分量中没有割边,且节点 \(x\) 满足 \(low[x]==dfn[x]\) ,则在以 \(x\) 为根的子树内没有一个节点有连边到该节点的祖先节点,所以仍在栈中的节点一定是以 \(x\) 为根的边双连通分量。
- 例题
- luogu P2860 [USACO06JAN] Redundant Paths G
- 简化题意:给定一个连通的无向图进行加边操作,使得每一对点之间都至少有两条相互分离的路径(两条路径没有一条重合的道路),即使得所有的节点都在环上(可能是不同的环),也可以理解为每个节点的入度至少为 \(2\) ,求最小的加边数。
- 考虑跑一遍 \(e-DCC\) 的缩点,找出所有的叶子节点(即入度为 \(1\) 的节点),设其个数为 \(leaf\) ,则结果为 $\left \lceil \frac{leaf}{2} \right \rceil $ 。
- 如图, \(1,3,4,5\) 为以 \(2\) 为根的树中的叶子节点( \(leaf=4\) ),则连接 \(1->3\) , \(4->5\) 为满足题意的一组解( \(\left \lceil \frac{leaf}{2} \right \rceil =2\) )。
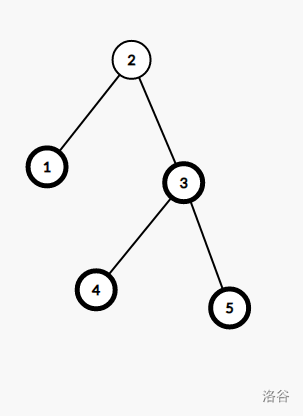
- 如图, \(1,3,4,5,6\) 为以 \(2\) 为根的树中的叶子节点( \(leaf=5\) ),则连接 \(1->3\) , \(4->5\) , \(3->6\) 为满足题意的一组解( \(\left \lceil \frac{leaf}{2} \right \rceil =3\) )。
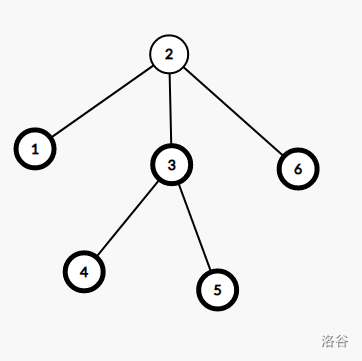
- 如图, \(1,3,4,5\) 为以 \(2\) 为根的树中的叶子节点( \(leaf=4\) ),则连接 \(1->3\) , \(4->5\) 为满足题意的一组解( \(\left \lceil \frac{leaf}{2} \right \rceil =2\) )。
- 代码
- CF652E Pursuit For Artifacts
- 要求每条边最多只能经过一次,容易知道本题可能需要缩点。
- 对于每个边双连通分量缩点,易知如果在一个边双连通分量中存在边权为 \(1\) 的边,则把缩成的这个点的点权赋值为 \(1\) ,然后从起点 \(c[a]\) 开始 \(DFS\) ,看到达终点 \(c[b]\) 时是否经过点权为 \(1\) 的点。然后注意一下每条边最多只能经过一次,开个 \(vis\) 数组判断即可。
- 代码
- luogu P2860 [USACO06JAN] Redundant Paths G
- 算法:把每一个边双连通分量缩成一个点使得原本的连通图变成一棵树(若原图不连通,则为树林),且树边就是原图的割边。其中满足 \(low[x]==dfn[x]\) 的节点 \(x\) ,这必定是一个边双连通分量的根。
参考资料:
学校的课件(不方便放出)
《算法竞赛进阶指南》———李煜东
本文来自博客园,作者:hzoi_Shadow,原文链接:https://www.cnblogs.com/The-Shadow-Dragon/p/17548536.html,未经允许严禁转载。
版权声明:本作品采用 「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0) 进行许可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号