【若归】背包dp做题笔记
前言：
现在决定未来，未来与过去无关。--波波
前置知识：
dd_engi的背包九讲（新版转载）
|
背包九讲——全篇详细理解与代码实现
背包问题 (附单调队列优化多重背包
|
背包问题入门(单调队列优化多重背包
题目来自学校OJ、洛谷、ybtOJ。
学校OJ：
A.采药
01背包（后面解题过程大部分均由01背包变形）板子题，加上一个滚动数组优化，没什么好说的。
$ 1<=i<=m,t>=j>=w[i]$
$f[j]=max(f[j],f[j-w[i]]+c[i]) $
#include<bits/stdc++.h>
using namespace std;
int w[10001],c[10001],f[10001];
int main()
{
int t,m,i,j;
cin>>t>>m;
for(i=1;i<=m;i++)
{
cin>>w[i]>>c[i];
}
for(i=1;i<=m;i++)
{
for(j=t;j>=w[i];j--)
{
f[j]=max(f[j],f[j-w[i]]+c[i]);
}
}
cout<<f[t]<<endl;
return 0;
}
B.开心的金明
与A类似，还是01背包板子，设第\(j\)件物品的价格为\(v[j]\)，重要度为\(w[j]\)，则第\(j\)件物品的价值为\(v[j]*w[j](j<=n)\)。
$ 1<=i<=m,n>=j>=v[i]$
$f[j]=max(f[j],f[j-v[i]]+p[i]) $
#include<bits/stdc++.h>
using namespace std;
int v[750001],p[750001],f[750001];
int main()
{
int n,m,i,j;
cin>>n>>m;
for(i=1;i<=m;i++)
{
cin>>v[i]>>p[i];
p[i]*=v[i];
}
for(i=1;i<=m;i++)
{
for(j=n;j>=v[i];j--)
{
f[j]=max(f[j],f[j-v[i]]+p[i]);
}
}
cout<<f[n]<<endl;
return 0;
}
C. 完全背包问题
完全背包板子（优化后面讲），因范围较小，选用不加优化的做法。
完全背包板子和和01背包板子仅有j的循环次序不同（注意一下，不要混淆），同时注意一下输出格式。
$ 1<=i<=n,w[i]<=j<=m$
$f[j]=max(f[j-w[i]]+c[i],f[j]) $
#include<bits/stdc++.h>
using namespace std;
int n,m,i,j,c[31],w[31],f[2001];
int main()
{
cin>>m>>n;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i];
}
for(i=1;i<=n;i++)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j-w[i]]+c[i],f[j]);
}
}
cout<<"max="<<f[m];
return 0;
}
D.竞赛总分
P2722 [USACO3.1]总分 Score Inflation
完全背包板子(同C),加强一下印象。
$ 1<=i<=n,w[i]<=j<=m$
$f[j]=max(f[j-w[i]]+c[i],f[j]) $
#include<bits/stdc++.h>
using namespace std;
int c[10001],w[10001],f[10001];
int main()
{
int n,m,i,j;
cin>>m>>n;
for(i=1;i<=n;i++)
{
cin>>c[i]>>w[i];
}
for(i=1;i<=n;i++)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j-w[i]]+c[i],f[j]);
}
}
cout<<f[m];
return 0;
}
E.砝码称重
考虑两种解法，一种是暴力（时间复杂度为各砝码数量相乘），一种是背包dp（最坏情况下为\(6*1000^2\)）；记得初始化，注意输出格式。
暴力：
建议不要采用这种方式，或者加上特判（未写）；如果是极限数据，就会被卡
#11
样例输入：65 34 34 23 23 21
样例输出：1000
#include<bits/stdc++.h>
using namespace std;
int c[1001];
int main()
{
int a[7],b[7],i,sum,ans=0;
cin>>a[1]>>a[2]>>a[3]>>a[4]>>a[5]>>a[6];
for(b[1]=0;b[1]<=a[1];b[1]++)
{
for(b[2]=0;b[2]<=a[2];b[2]++)
{
for(b[3]=0;b[3]<=a[3];b[3]++)
{
for(b[4]=0;b[4]<=a[4];b[4]++)
{
for(b[5]=0;b[5]<=a[5];b[5]++)
{
for(b[6]=0;b[6]<=a[6];b[6]++)
{
sum=b[1]+b[2]*2+b[3]*3+b[4]*5+b[5]*10+b[6]*20;
if(c[sum]==0)
{
c[sum]=1;
ans++;
}
}
}
}
}
}
}
ans--;
cout<<"Total="<<ans;
return 0;
}
背包dp：
思路是枚举每个砝码数量，若\(f[k]\)存在,则\(f[k+b[i]]\)一定存在；如果数据范围较大，可将f数组的类型从int改为bool。
#include<bits/stdc++.h>
using namespace std;
int a[7],b[7]={0,1,2,3,5,10,20},f[1001];
int main()
{
int i,j,k,ans=0;
for(i=1;i<=6;i++)
{
cin>>a[i];
}
f[0]=1;
for(i=1;i<=6;i++)
{
for(j=1;j<=a[i];j++)
{
for(k=1000;k>=0;k--)
{
if(f[k]==1)
{
if(f[k+b[i]]==0)
{
f[k+b[i]]=1;
ans++;
}
}
}
}
}
cout<<"Total="<<ans;
return 0;
}
F.最小乘车费用
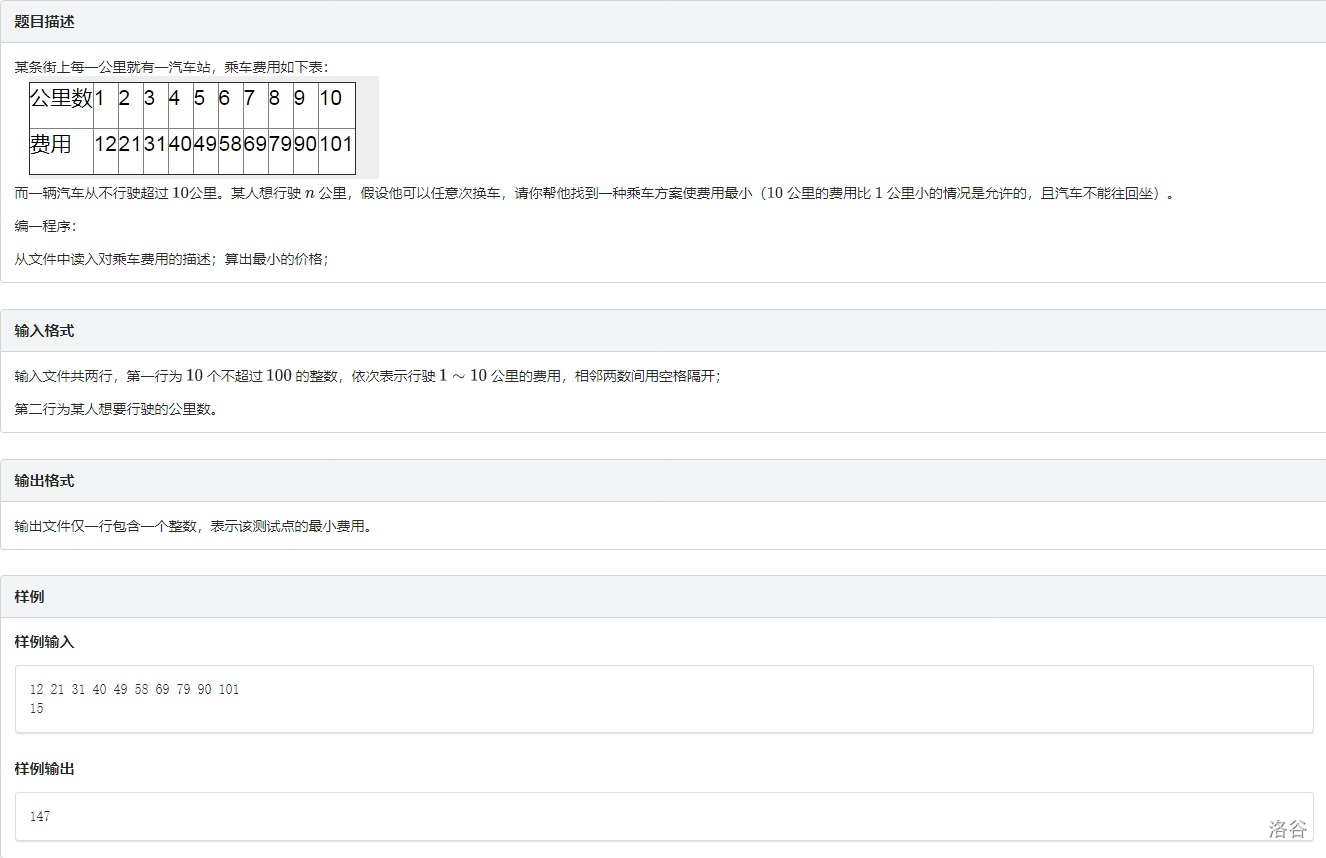
完全背包变形，枚举每种情况下的距离以达到状态转移。
$ 1<=i<=10,i<=j<=n$
$ f[j]=min(f[j-i]+w[i],f[j])$
#include<bits/stdc++.h>
using namespace std;
int f[10001],w[11];
int main()
{
int n,i,j;
memset(f,0x3f3f3f3f,sizeof(f));
f[0]=0;
for(i=1;i<=10;i++)
{
cin>>w[i];
}
cin>>n;
for(i=1;i<=10;i++)
{
for(j=i;j<=n;j++)
{
f[j]=min(f[j-i]+w[i],f[j]);//用f[j-i]+w[i]和f[j]取最小值更新f[j].f[j-i]表示到j-i的最短花费，加上w[i]即可(走i公里需要的花费）。
}
}
cout<<f[n];
return 0;
}
G.逃亡的准备
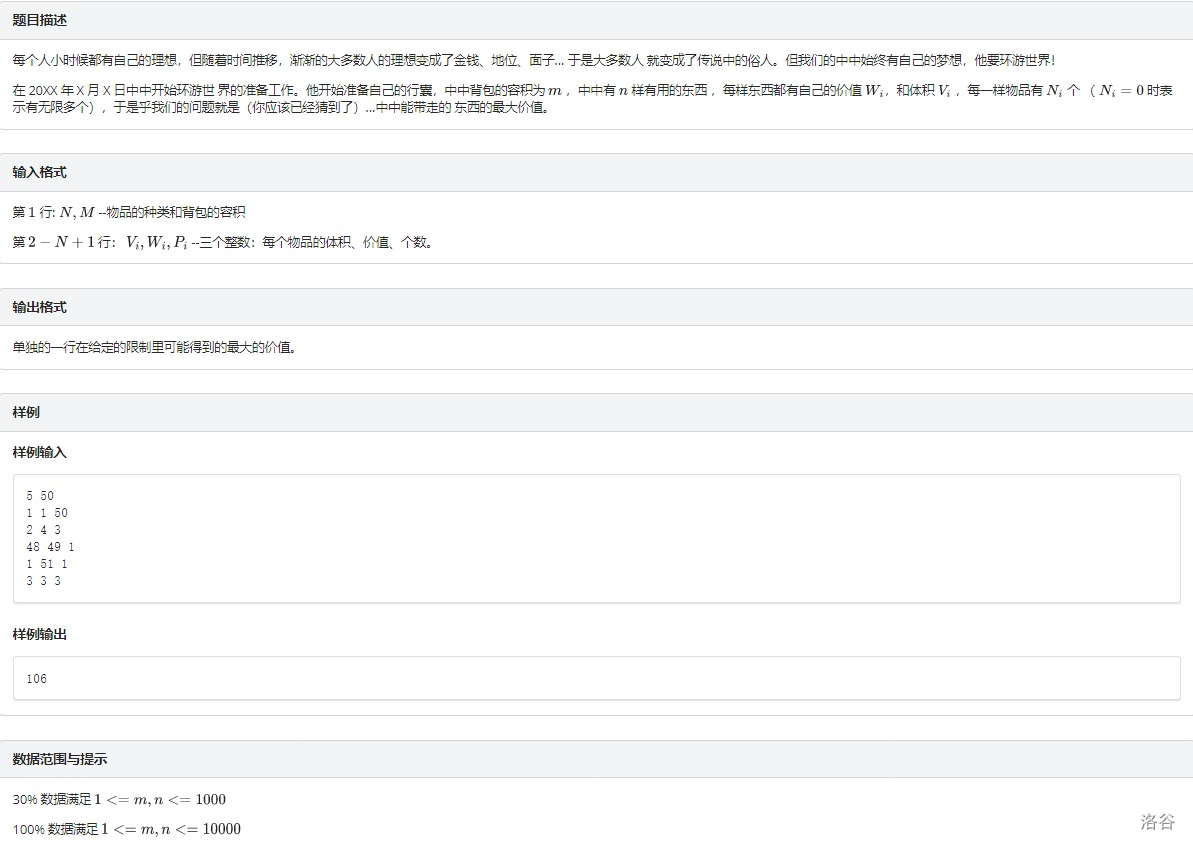
初看到这道题以为是混合背包板子，然后就TLE了。（小声bb：我还以为是测评姬波动，前前后后交了170+次）
后来考2022CSP前，将混合背包的01背包和多重背包进行了二进制优化，于是AC。（如果数据再ex亿点，可能要用单调队列优化）
\(1<=i<=n\)
\(if(p[i]==0)\) $ v[i]<=j<=m$ \(f[j]=max(f[j],f[j-v[i]]+w[i])\)
\(else\) 详见代码
#include <bits/stdc++.h>
using namespace std;
int f[10001],v[10001],w[10001],p[10001];
int main()
{
int n,m,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>v[i]>>w[i]>>p[i];
if(p[i]==0)//完全背包
{
for(j=v[i];j<=m;j++)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
else//01背包可以当作多重背包来处理
{
for(k=1;k<=p[i];k*=2)
{
for(j=m;j>=k*v[i];j--)
{
f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
}
p[i]-=k;
}
if(p[i]>0)
{
for(j=m;j>=p[i]*v[i];j--)
{
f[j]=max(f[j],f[j-p[i]*v[i]]+p[i]*w[i]);
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
H.庆功会
不加优化的多重背包即可，优化详见G。
\(1<=i<=n,m>=j>=0,0<=k<=num[i]\)
$ if(j-k*w[i]>=0)$ \(f[j]=max(f[j],f[j-k*w[i]]+k*c[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[10001],c[10001],num[10001],f[10001];
int main()
{
int m,n,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i]>>num[i];
}
for(i=1;i<=n;i++)
{
for(j=m;j>=0;j--)
{
for(k=0;k<=num[i];k++)
{
if(j-k*w[i]>=0)//很重要，避免RE
{
f[j]=max(f[j],f[j-k*w[i]]+k*c[i]);
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
I.混合背包
不加优化的混合背包即可，优化详见G。
\(1<=i<=n\)
\(if(num[i]==1)\) $ m>=j>=w[j]$ \(f[j]=max(f[j],f[j-w[i]]+c[i])\)
\(if(num[i]==0)\) $ w[i]<=j<=m$ \(f[j]=max(f[j],f[j-w[i]]+c[i])\)
\(if(num[i]>1)\) \(m>=j>=0,0<=k<=num[i]\) \(if(j-k*w[i]>=0)\) \(f[j]=max(f[j],f[j-k*w[i]]+k*c[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[10001],c[10001],num[10001],f[10001];
int main()
{
int m,n,i,j,k;
cin>>m>>n;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i]>>num[i];
}
for(i=1;i<=n;i++)
{
if(num[i]==1)
{
for(j=m;j>=w[i];j--)
{
f[j]=max(f[j],f[j-w[i]]+c[i]);
}
}
else
{
if(num[i]==0)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j],f[j-w[i]]+c[i]);
}
}
else
{
for(j=m;j>=0;j--)
{
for(k=0;k<=num[i];k++)
{
if(j-k*w[i]>=0)
{
f[j]=max(f[j],f[j-k*w[i]]+k*c[i]);
}
}
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
J.NASA的食物计划
二维费用的背包板子。（教练说非常简单）
\(1<=i<=q,p>=j>=w[i],q>=k>=v[i]\) \(f[j][k]=max(f[j][k],f[j-w[i]][k-v[i]]+c[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[401],v[401],c[401],f[401][401];
int main()
{
int p,q,n,i,j,k;
cin>>p>>q>>n;
for(i=1;i<=n;i++)
{
cin>>w[i]>>v[i]>>c[i];
}
for(i=1;i<=q;i++)
{
for(j=p;j>=w[i];j--)
{
for(k=q;k>=v[i];k--)
{
f[j][k]=max(f[j][k],f[j-w[i]][k-v[i]]+c[i]);
}
}
}
cout<<f[p][q];
return 0;
}
K. 分组背包
分组背包板子。
每组物品有若干种策略：选本组的某一件，或者一件也不选。即设 \(f[k][j]\) 表示前 \(k\) 组物品花费费用 \(j\) 能取得的最大权值，则有$ f[k][j]=max(f[k-1][j],f[k-1][j-w[i]+c[i]|物品i属于第k组)$。接着将其用滚动数组优化即可（转换为一维数组）。
\(1<=k<=t,v>=j>=0,1<=i<=group[k][0]\)
\(if(j>=w[group[i][k]]) f[j]=max(f[j],f[j-w[group[i][k]]]+c[group[i][k]])\)
#include<bits/stdc++.h>
using namespace std;
int group[1001][1001],w[1001],c[1001],f[1001];
int main()
{
int v,n,t,i,j,k,p,q;
cin>>v>>n>>t;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i]>>p;
group[p][0]++;
group[p][group[p][0]]=i;
}
for(i=1;i<=t;i++)
{
for(j=v;j>=0;j--)
{
for(k=1;k<=group[i][0];k++)
{
q=group[i][k];
if(j>=w[q])
{
f[j]=max(f[j],f[j-w[q]]+c[q]);
}
}
}
}
cout<<f[v]<<endl;
return 0;
}
L.新年趣事之打牌
01背包的变形，判断是否有解及多组解，同时进行记录，方便后面输出。
#include<bits/stdc++.h>
using namespace std;
int w[100001],s[100001],f[100001],ans[100001];
int main()
{
int n,num,i,j,sum;
cin>>num>>n;
for(i=1;i<=n;i++)
{
cin>>w[i];
}
s[0]=1;//初始化
for(i=1;i<=n;i++)//01背包
{
for(j=num;j>=w[i];j--)
{
if(s[j-w[i]]!=0)
{
s[j]+=s[j-w[i]];
if(f[j]==0)
{
f[j]=i;//初始化+记录路径
}
}
}
}
if(s[num]==0)//无解
{
cout<<"0";
}
if(s[num]==1)//有解
{
sum=num;
while(sum>0)//记录路径（纸牌）
{
ans[f[sum]]=1;
sum-=w[f[sum]];
}
for(i=1;i<=n;++i)//输出
{
if(ans[i]==0)
{
cout<<i<<" ";
}
}
}
if(s[num]>1)//有多组解
{
cout<<"-1";
}
return 0;
}
M. 积木城堡
01背包变形，判断是否有解。
#include<bits/stdc++.h>
using namespace std;
int h[10001],num[10001],f[10001];
int main()
{
int n,ans=0x3f3f3f3f,sum,i,j,k,p,flag=0;//初始化
cin>>n;
for(i=1;i<=n;i++)
{
memset(f,0,sizeof(f));//每次循环都要清空
memset(h,0,sizeof(h));//每次循环都要清空（这条语句可要可不要，但还是带上的好）
f[0]=1;//初始化
p=1;
sum=0;
while(cin>>h[p])
{
if(h[p]==-1)
{
break;
}
else
{
sum+=h[p];
}
p++;
}
p--;//因为读入结束后，p会比实际长度多1，故p--
ans=min(ans,sum);//ans为查询的最大值
for(j=1;j<=p;j++)//01背包
{
for(k=sum;k>=h[j];k--)
{
if(f[k-h[j]]==1)
{
f[k]=1;
}
}
}
for(j=sum;j>=1;j--)//标记下
{
if(f[j]==1)
{
num[j]++;
}
}
}
for(i=ans;i>=1;i--)
{
if(num[i]==n)//有解
{
cout<<i;
flag=1;
break;
}
}
if(flag==0)//无解
{
cout<<"0";
}
return 0;
}
洛谷：
注意数据范围有亿点大，不能用正常的01背包解决。换一种方式，让f数组用来储存容量，即\(f[i]\)用来储存价值为 \(i\) 时所需的最小容量。
$ 1<=i<=t,1000*t>=j>=c[i]$
\(f[j]=max(f[j],f[j-c[i]]+w[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[1000001],c[1000001],f[1000001];
int main()
{
int t,m,i,j;
cin>>t>>m;
memset(f,0x3f,sizeof(f));
for(i=1;i<=t;i++)
{
cin>>w[i]>>c[i];
}
f[0]=0;
for(i=1;i<=t;i++)
{
for(j=1000*t;j>=c[i];j--)
{
f[j]=min(f[j],f[j-c[i]]+w[i]);
}
}
for(i=1000*t;i>0;i--)
{
if(f[i]<=m)
{
cout<<i;
break;
}
}
return 0;
}
单调队列优化多重背包板子
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
int f[100001],g[100001],w[100001],v[100001],p[100001];
int main()
{
int n,m,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>v[i]>>w[i]>>p[i];
if(p[i]==0)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j],f[j-w[i]]+v[i]);
}
}
else
{
memcpy(g,f,sizeof(f));
for(j=0;j<w[i];j++)
{
deque<int>q;
for(k=0;k<=(m-j)/w[i];k++)
{
if(q.empty()==0&&q.front()<k-p[i])
{
q.pop_front();
}
while(q.empty()==0&&g[j+q.back()*w[i]]-q.back()*v[i]<=g[j+k*w[i]]-k*v[i])
{
q.pop_back();
}
q.push_back(k);
f[j+k*w[i]]=g[j+q.front()*w[i]]+(k-q.front())*v[i];
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
/*
#include <bits/stdc++.h>
using namespace std;
int f[100001],w[100001],v[100001],p[100001];
int main()
{
int n,m,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>v[i]>>w[i]>>p[i];
if(p[i]==0)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j],f[j-w[i]]+v[i]);
}
}
else
{
for(k=1;k<=p[i];k*=2)
{
for(j=m;j>=k*w[i];j--)
{
f[j]=max(f[j],f[j-k*w[i]]+k*v[i]);
}
p[i]-=k;
}
if(p[i]>0)
{
for(j=m;j>=p[i]*w[i];j--)
{
f[j]=max(f[j],f[j-p[i]*w[i]]+p[i]*v[i]);
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
*/
本文来自博客园，作者：hzoi_Shadow，原文链接：https://www.cnblogs.com/The-Shadow-Dragon/p/17470317.html，未经允许严禁转载。
版权声明：本作品采用 「署名-非商业性使用-相同方式共享 4.0 国际」许可协议（CC BY-NC-SA 4.0） 进行许可。
