图像直方图
看到这个题目的瞬间，你会不会这样想:为什么我们要分析图像的直方图？将从以下几个方面进行合理的解释：
（1）定义
灰度直方图是灰度级的函数，描述的是图像中具有该灰度级的像元的个数。确定图像像元的灰度值范围，以适当的灰度间隔为单位将其划分为若干等级，以横轴表示灰度级，以纵轴表示每一灰度级具有的像元数或该像元数占总像元数的比例值，做出的条形统计图即为灰度直方图。
（2）性质
- 直方图反映了图像中的灰度分布规律。它描述每个灰度级具有的像元个数，但不包含这些像元在图像中的位置信息。
- 任何一幅特定的图像都有唯一的直方图与之对应，但不同的图像可以有相同的直方图。
- 如果一幅图像有两个不相连的区域组成，并且每个区域的直方图已知，则整幅图像的直方图是该两个区域的直方图之和
（3）直方图的应用
- 对于每幅图像都可做出其灰度直方图。
- 根据直方图的形态可以大致推断图像质量的好坏。由于图像包含有大量的像元，其像元灰度值的分布应符合概率统计分布规律。假定像元的灰度值是随机分布的，那么其直方图应该是正态分布。
- 图像的灰度值是离散变量，因此直方图表示的是离散的概率分布。若以各灰度级的像元数占总像元数的比例值为纵坐标轴做出图像的直方图，将直方图中各条形的最高点连成一条外轮廓线，纵坐标的比例值即为某灰度级出现的概率密度，轮廓线可近似看成图像相应的连续函数的概率分布曲线。
一 reshape函数与flatten函数
假设我们先生成一个一维数组：
vec=np.arange(15)
print (vec)
结果为：[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
如果我们要把这个一维数组，变成一个3*5二维矩阵，我们可以使用reshape来实现
mat= vec.reshape(3,5)
print(mat)
结果为：
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
现在如果我们返过来，知道一个二维矩阵，要变成一个一维数组，就不能用reshape了，只能用flatten. 我们来看两者的区别
a1=mat.reshape(1,-1) #-1表示为任意，让系统自动计算
print (a1)
a2=mat.flatten()
print (a2)
结果为：
[[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]]
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
可以看出，用reshape进行变换，实际上变换后还是二维数组，两个方括号，因此只能用flatten.我们要对图像求直方图，就需要先把图像矩阵进行flatten操作，使之变为一维数组，然后再进行统计。
二 灰度图像直方图
绘图都可以调用matplotlib.pyplot库来进行，其中的hist函数可以直接绘制直方图。调用方式如下：
n, bins, patches = plt.hist(arr, bins=50, normed=1, facecolor='green', alpha=0.75)
hist的参数非常多，但常用的就这五个，只有第一个是必须的，后面四个可选
- arr: 需要计算直方图的一维数组
- bins: 直方图的柱数，可选项，默认为10
- normed: 是否将得到的直方图向量归一化。默认为0
- facecolor: 直方图颜色
- alpha: 透明度
返回值 ：
- n: 直方图向量，是否归一化由参数设定
- bins: 返回各个bin的区间范围
- patches: 返回每个bin里面包含的数据，是一个list
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
img=np.array(Image.open('D:\\杨幂.jpg').convert('L'))
plt.figure("杨幂")
arr=img.flatten()
n, bins, patches = plt.hist(arr, bins=256, normed=1, facecolor='green', alpha=0.75)
plt.show()
结果如下图所示：
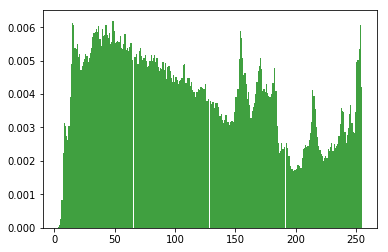
三 彩色图片直方图
实际上是和灰度直方图一样的，只是分别画出三通道的直方图，然后叠加在一起。
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
src=Image.open('D:\\杨幂.jpg')
r,g,b,a=src.split()
plt.figure("杨幂")
ar = np.array(r).flatten()
plt.hist(ar, bins = 256, normed = 1,facecolor = 'r',edgecolor = 'r',hold = 1)
ag = np.array(g).flatten()
plt.hist(ag, bins = 256, normed = 1, facecolor = 'g',edgecolor = 'g',hold = 1)
ab = np.array(b).flatten()
plt.hist(ab, bins = 256, normed = 1, facecolor = 'b',edgecolor = 'b')
plt.show()
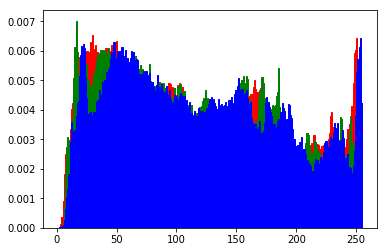
结果如下图所示：
