无监督学习：Neighbor Embedding(邻域嵌套)

一 Manifold Learning

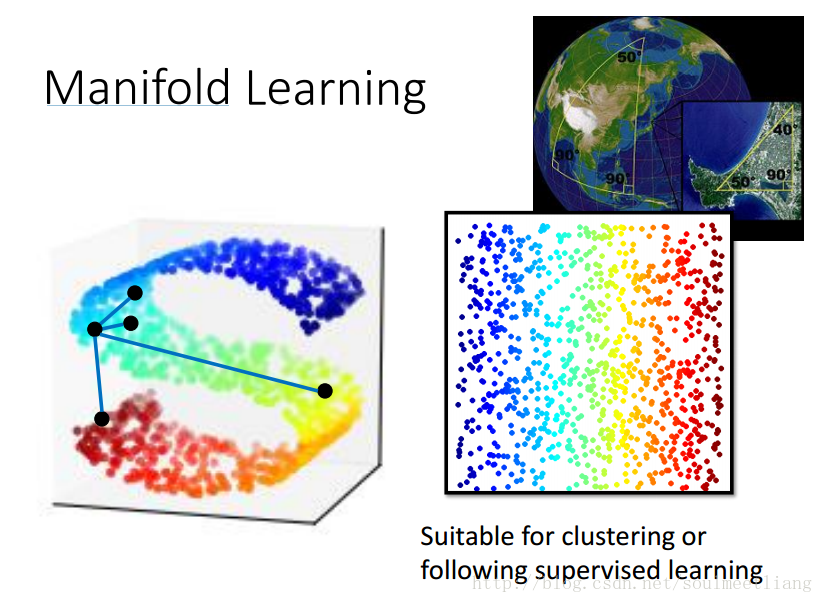
我们要做的是非线性的降维，data是分布在低维空间里面，只是被扭曲到了高维空间。 比如地球的表面是一个二维平面，但是被塞到一个三维空间中。 Manifold就是把S型摊平，将高维空间内的低维数据展开，这样才能计算点对点的距离。

 

二 几种方法

2.1 Locally Linear Embedding (LLE)

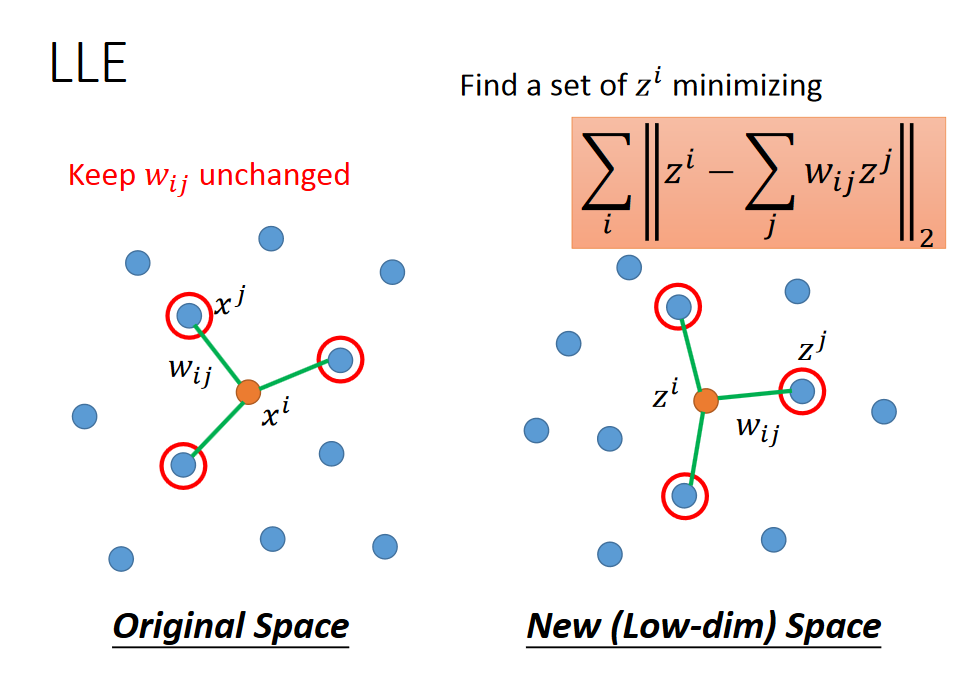
在原来的空间里面，有某点Xi，然后找到它的neighbor Xj，通过minimizing来找出Wij，再在降维后的空间里，找到基于不变的Wij参数的Zi和Zj。

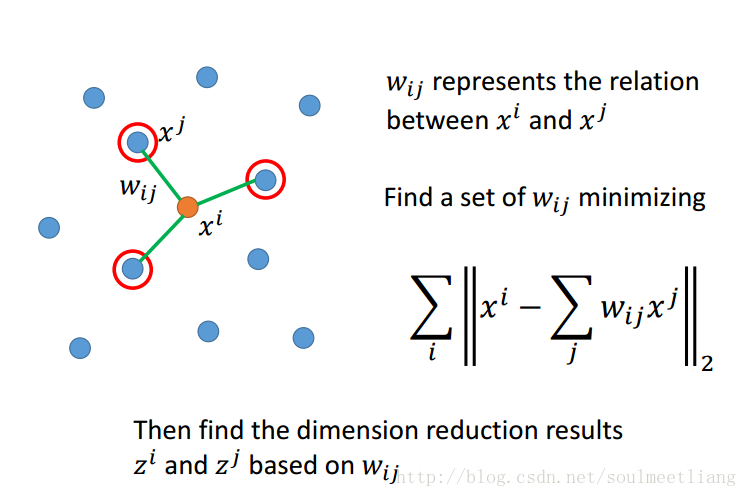
形象的比喻：

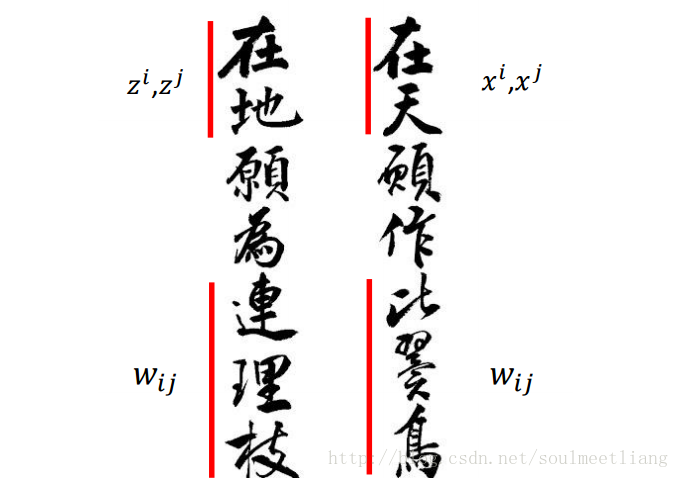
转换过程：找到一个Zi，在原有的Wij不变的参数下，能有一组邻居使该公式minimize

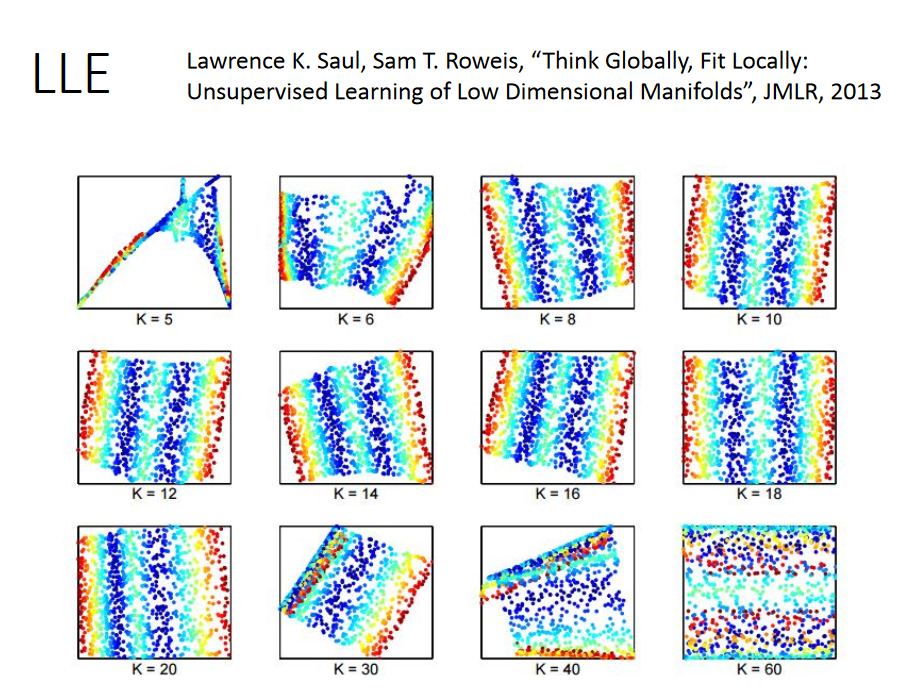
LLE要选一个刚刚好的neighbor，K太大并不好，此时会有一些关系太弱的点，transform后不能被keep住，也就是说他们不是“比翼鸟”与“连理枝”。

2.2 Laplacian Eigenmaps

2.3 T-distributed Stochastic Neighbor Embedding (t-SNE)

t-SNE要解决什么样的问题呢？ 前面的有一个最大的问题：他们只假设了相似的点接近，但没有说不同的点就一定要分离。 两个例子，都挤成一团。

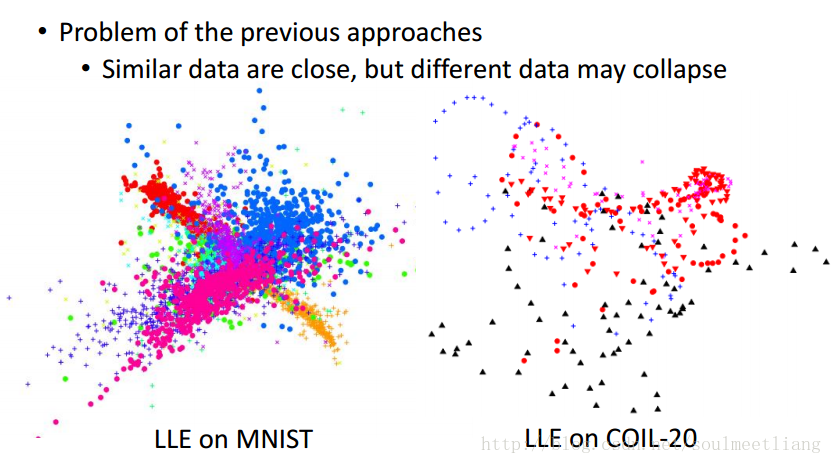
那么t-SNE是怎样计算的？

t-SNE similarity的神妙选择，从图中可以看出，使较远的data point距离被拉的更大。

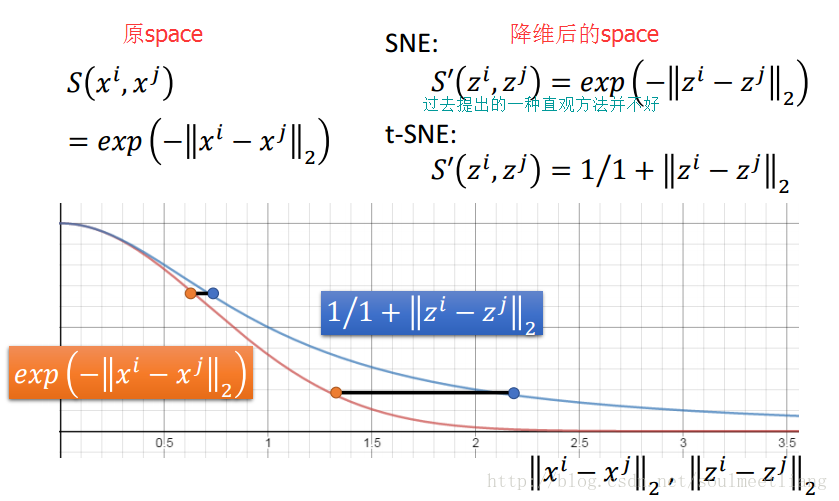
经典实例效果如图：

参考：

http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/tsne%20%28v2%29.pdf

https://blog.csdn.net/soulmeetliang/article/details/73441615