模型误差分析

一 Review

二 Estimator（估计）

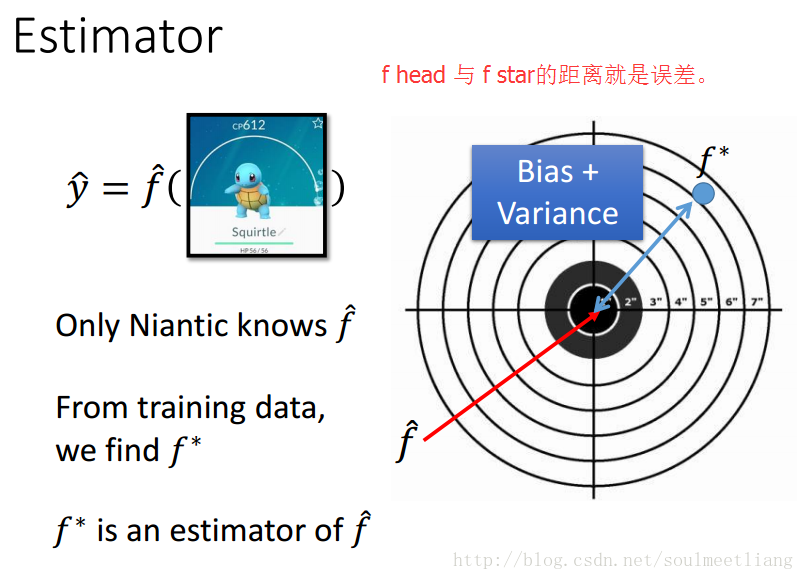
下边补充一些数理统计的知识：

---

 

由上图可以看出，样本的均值一般是不等于随机变量的期望（除非你有无穷多个样本点），而样本均值的期望是与随机变量的期望是一致的。样本均值偏离随机变量期望u的程度是由下图中的var[m]所决定的，这个值取决于sample的数量。

 

 

variance估计的期望值始终小于variance的值，随着N的增大，差距逐渐变小。

---

 

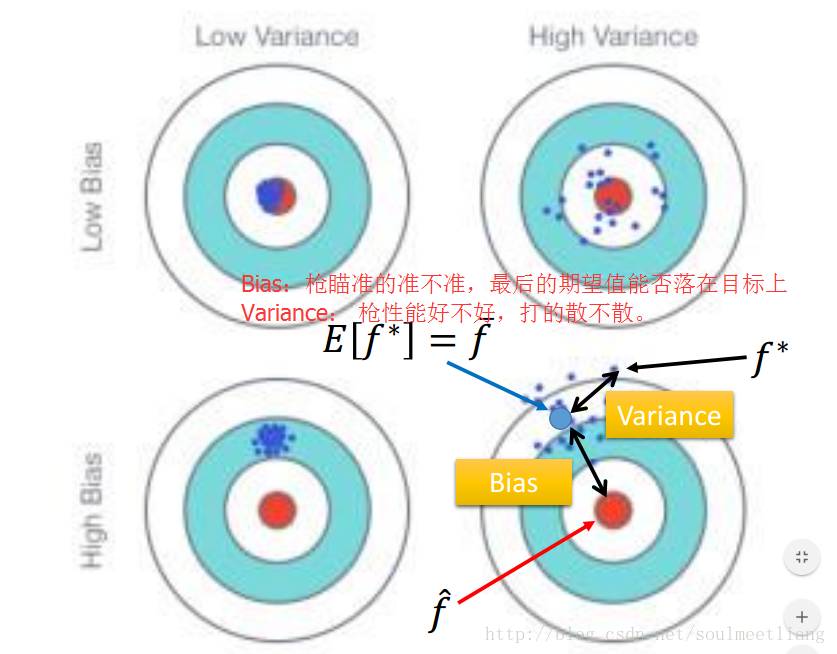
Bias and Variance of Estimator

写到这里可能有小伙伴要问了，你不就只能做一次实验吗，宝可梦长大以后是不可逆的啊，你怎么会怎么找很多个f*呢，我们可以假设有很多的平行宇宙

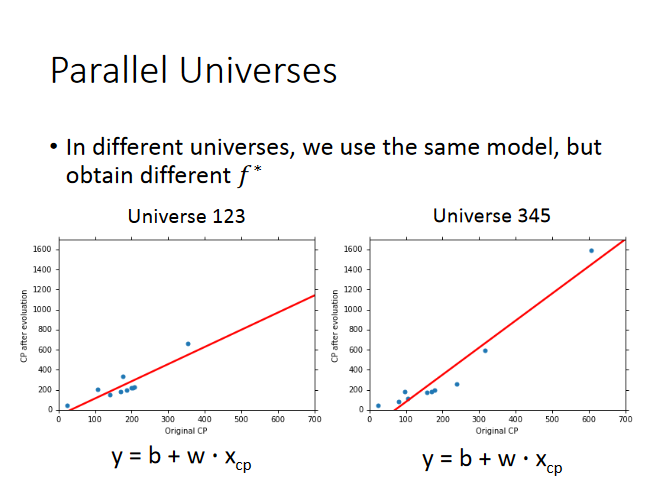
在100个平行宇宙中获得的f*长什么样呢，如下所示：

可以看出，当使用简单的model的时候，能满足training data的曲线，散布较少，varinance较小，而复杂的model散布较广，variance很大。

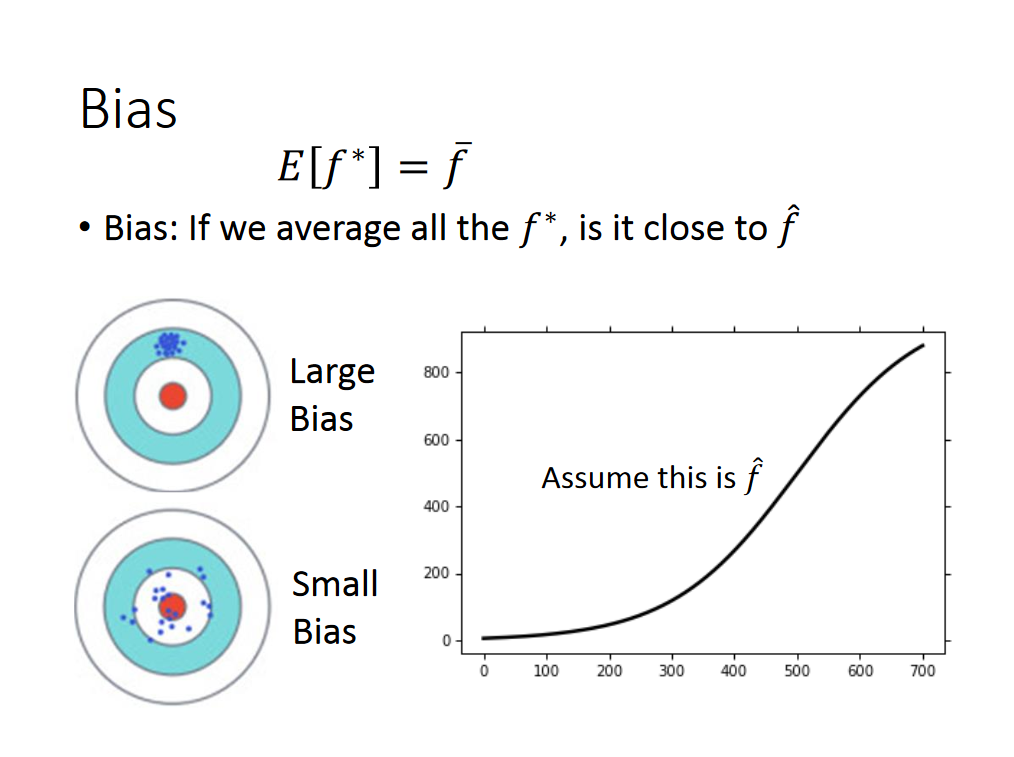
讨论完variance，我们再来谈谈bias。我们不知道真实的f长什么样，只有开发宝可梦的程序员知道，我们假设如下图所示：

bias v.s. variance

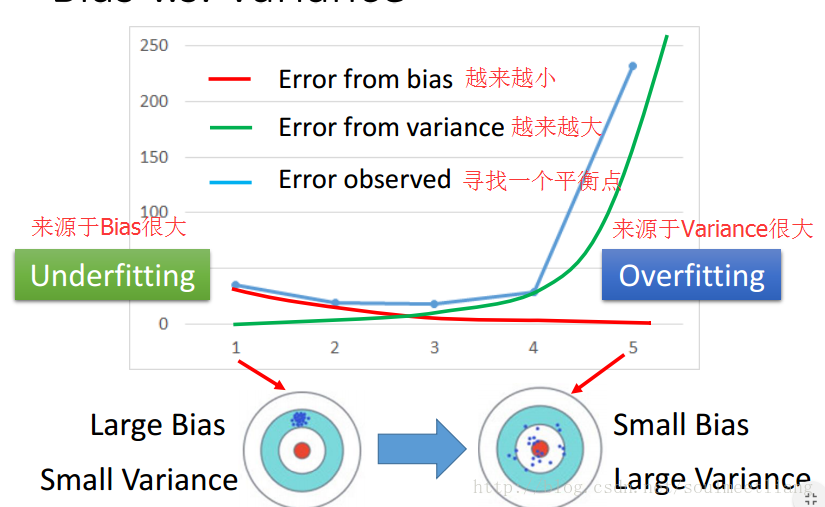
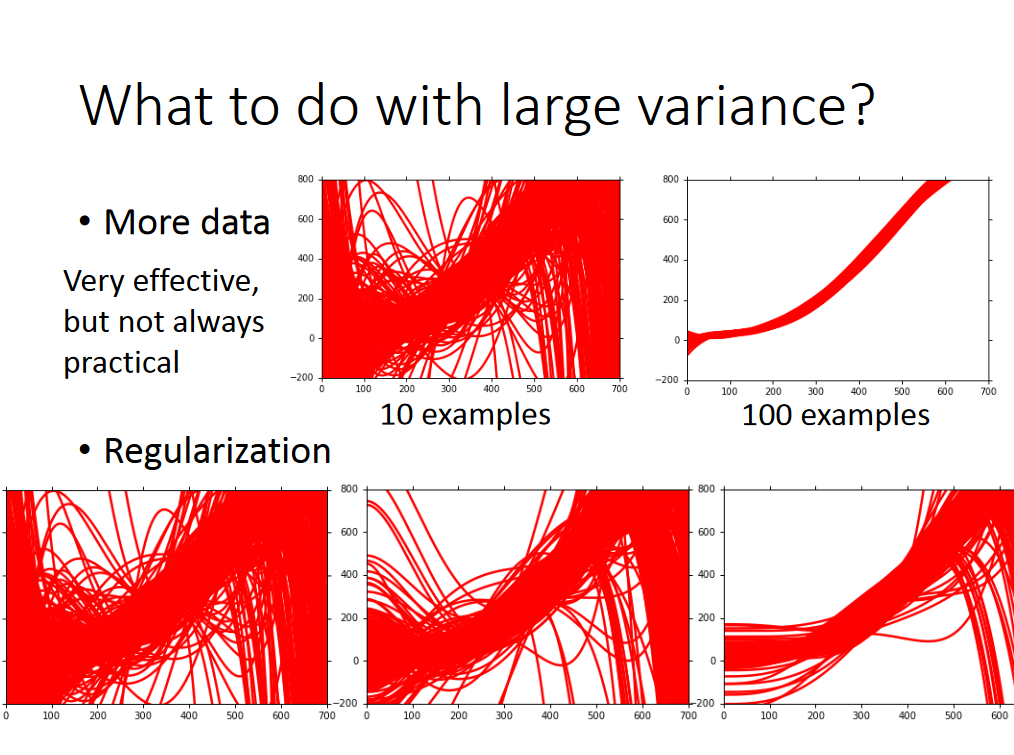
那么怎么选择合适的模型呢？下边这个方式不建议：

对于上图的说明，你可能会有一些困惑，现在以作业为例进行讲解：

　　既然上述方式得出的model不可靠，所以我们更多的是选择交叉验证这种方式。将training set 分成两部分，其中training set用作训练model，validation set用于选择model。当我们选定好选择的model以后（比如我们选择的是model3），我们可以使用全部的training set的数据在训练一遍我们的model，然后我们就可以在public testing set上测试我们的数据，有可能error会大于百分之五十（但是反映真实的测试情况，即反映private testing set），此时不建议重新返回训练我们的model，这是因为我们的model已经考虑将public testing set 的bias考虑了进来。

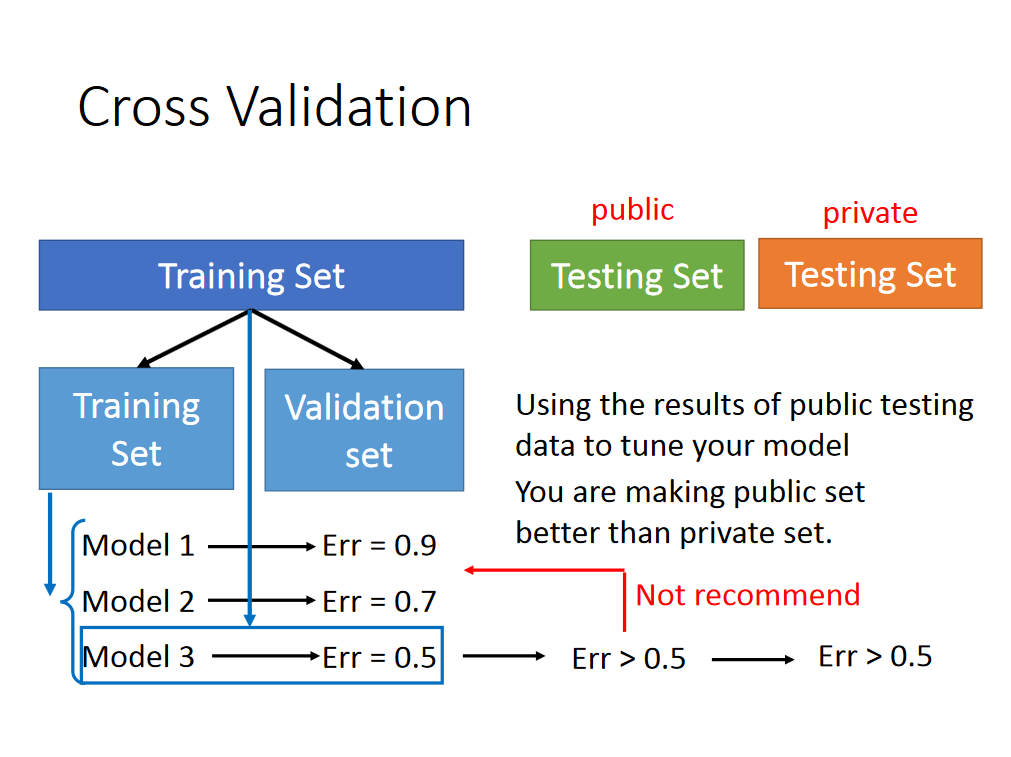
假如我们将training set分的不好怎么办？可以采用以下的方式：

参考：https://blog.csdn.net/soulmeetliang/article/details/72834429