RPN（区域生成网络）
转：懒人元（侵删）
RPN全称是Region Proposal Network，Region Proposal的中文意思是“区域选取”，也就是“提取候选框”的意思，所以RPN就是用来提取候选框的网络。
1. RPN的意义
RPN第一次出现在世人眼中是在Faster RCNN这个结构中，专门用来提取候选框，在RCNN和Fast RCNN等物体检测架构中，用来提取候选框的方法通常是Selective Search，是比较传统的方法，而且比较耗时，在CPU上要2s一张图。所以作者提出RPN，专门用来提取候选框，一方面RPN耗时少，另一方面RPN可以很容易结合到Fast RCNN中，称为一个整体。
RPN的引入，可以说是真正意义上把物体检测整个流程融入到一个神经网络中，这个网络结构叫做Faster RCNN； Faster RCNN = RPN + Fast RCNN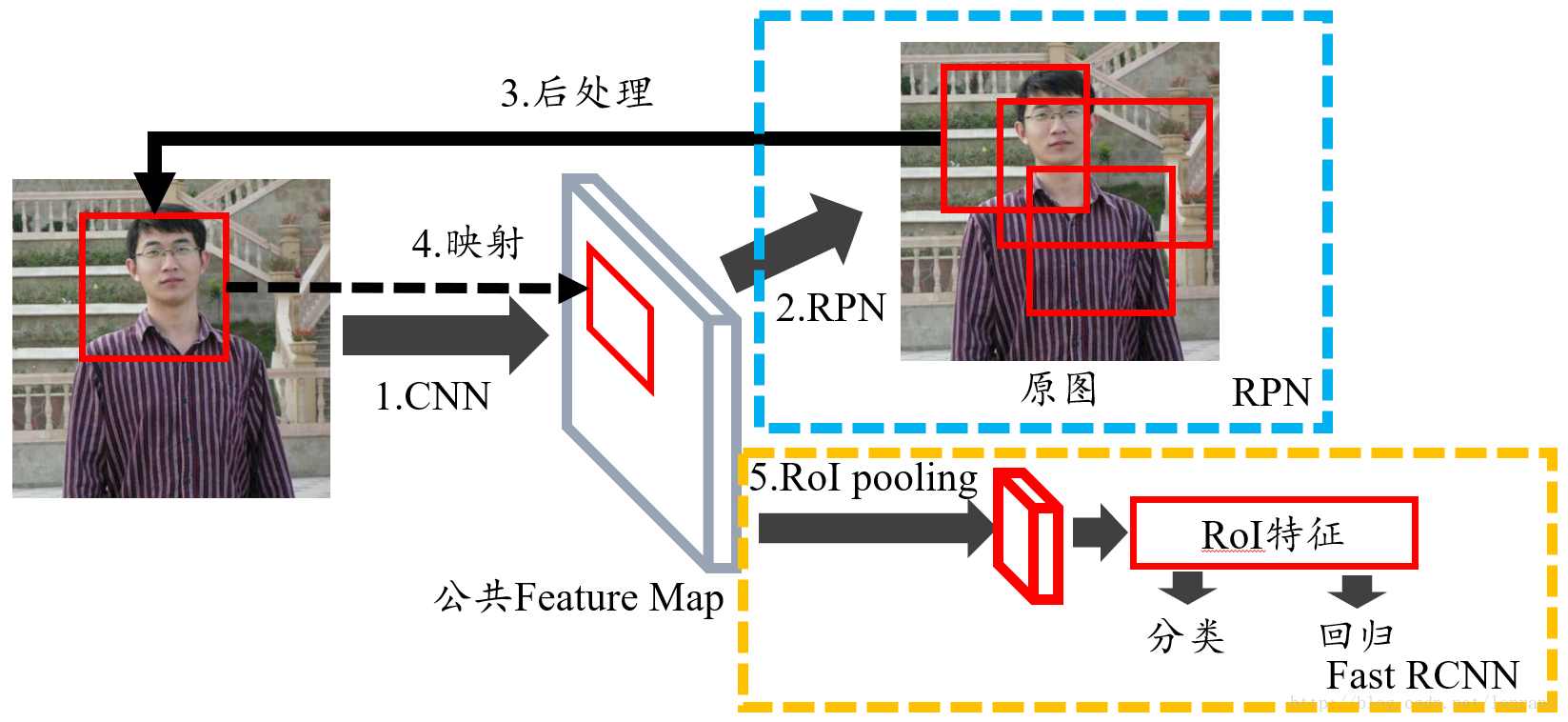 
图1 Faster RCNN的整体结构
我们不难发现，RPN在整个Faster RCNN中的位置，处于中间部分；
2. RPN的运作机制
我们先来看看Faster RCNN原文中的图：
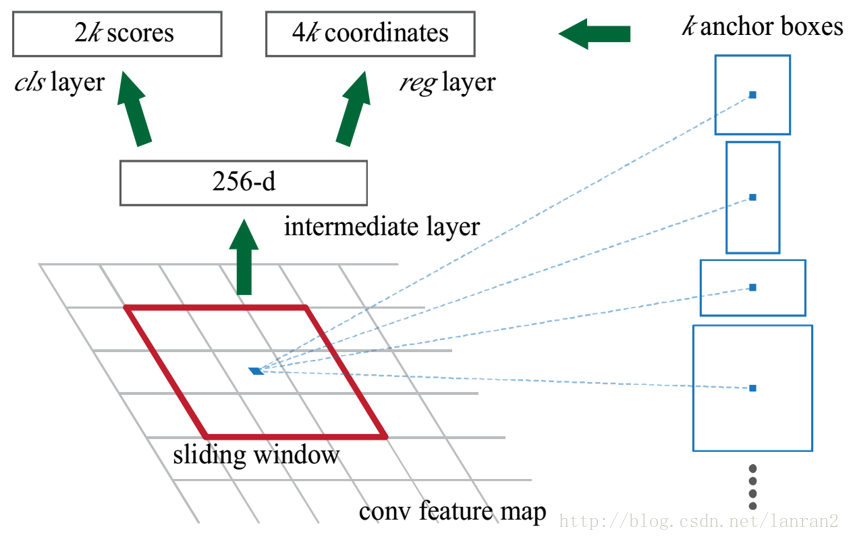
图2 RPN的结构
图2展示了RPN的整个过程，一个特征图经过sliding window处理，得到256维特征，然后通过两次全连接得到结果2k个分数和4k个坐标；相信大家一定有很多不懂的地方；我把相关的问题一一列举：
- RPN的input 特征图指的是哪个特征图？
- 为什么是用sliding window？文中不是说用CNN么？
- 256维特征向量如何获得的？
- 2k和4k中的k指的是什么？
- 图右侧不同形状的矩形和Anchors又是如何得到的？
首先回答第一个问题，RPN的输入特征图就是图1中Faster RCNN的公共Feature Map，也称共享Feature Map，主要用以RPN和RoI Pooling共享；
对于第二个问题，我们可以把3x3的sliding window看作是对特征图做了一次3x3的卷积操作，最后得到了一个channel数目是256的特征图，尺寸和公共特征图相同，我们假设是256 x （H x W）；
对于第三个问题，我们可以近似的把这个特征图看作有H x W个向量，每个向量是256维，那么图中的256维指的就是其中一个向量，然后我们要对每个特征向量做两次全连接操作，一个得到2个分数，一个得到4个坐标，由于我们要对每个向量做同样的全连接操作，等同于对整个特征图做两次1 x 1的卷积，得到一个2 x H x W和一个4 x H x W大小的特征图，换句话说，有H x W个结果，每个结果包含2个分数和4个坐标；
图3 问题1，2，3的解答描述图
这里我们需要解释一下为何是2个分数，因为RPN是提候选框，还不用判断类别，所以只要求区分是不是物体就行，那么就有两个分数，前景（物体）的分数，和背景的分数；
我们还需要注意：4个坐标是指针对原图坐标的偏移，首先一定要记住是原图；
此时读者肯定有疑问，原图哪里来的坐标呢？
这里我要解答最后两个问题了：
首先我们知道有H x W个结果，我们随机取一点，它跟原图肯定是有个一一映射关系的，由于原图和特征图大小不同，所以特征图上的一个点对应原图肯定是一个框，然而这个框很小，比如说8 x 8，这里8是指原图和特征图的比例，所以这个并不是我们想要的框，那我们不妨把框的左上角或者框的中心作为锚点（Anchor），然后想象出一堆框，具体多少，聪明的读者肯定已经猜到，K个，这也就是图中所说的K anchor boxes（由锚点产生的K个框）；换句话说，H x W个点，每个点对应原图有K个框，那么就有H x W x k个框默默的在原图上，那RPN的结果其实就是判断这些框是不是物体以及他们的偏移；那么K个框到底有多大，长宽比是多少？这里是预先设定好的，共有9种组合，所以k等于9，最后我们的结果是针对这9种组合的，所以有H x W x 9个结果，也就是18个分数和36个坐标；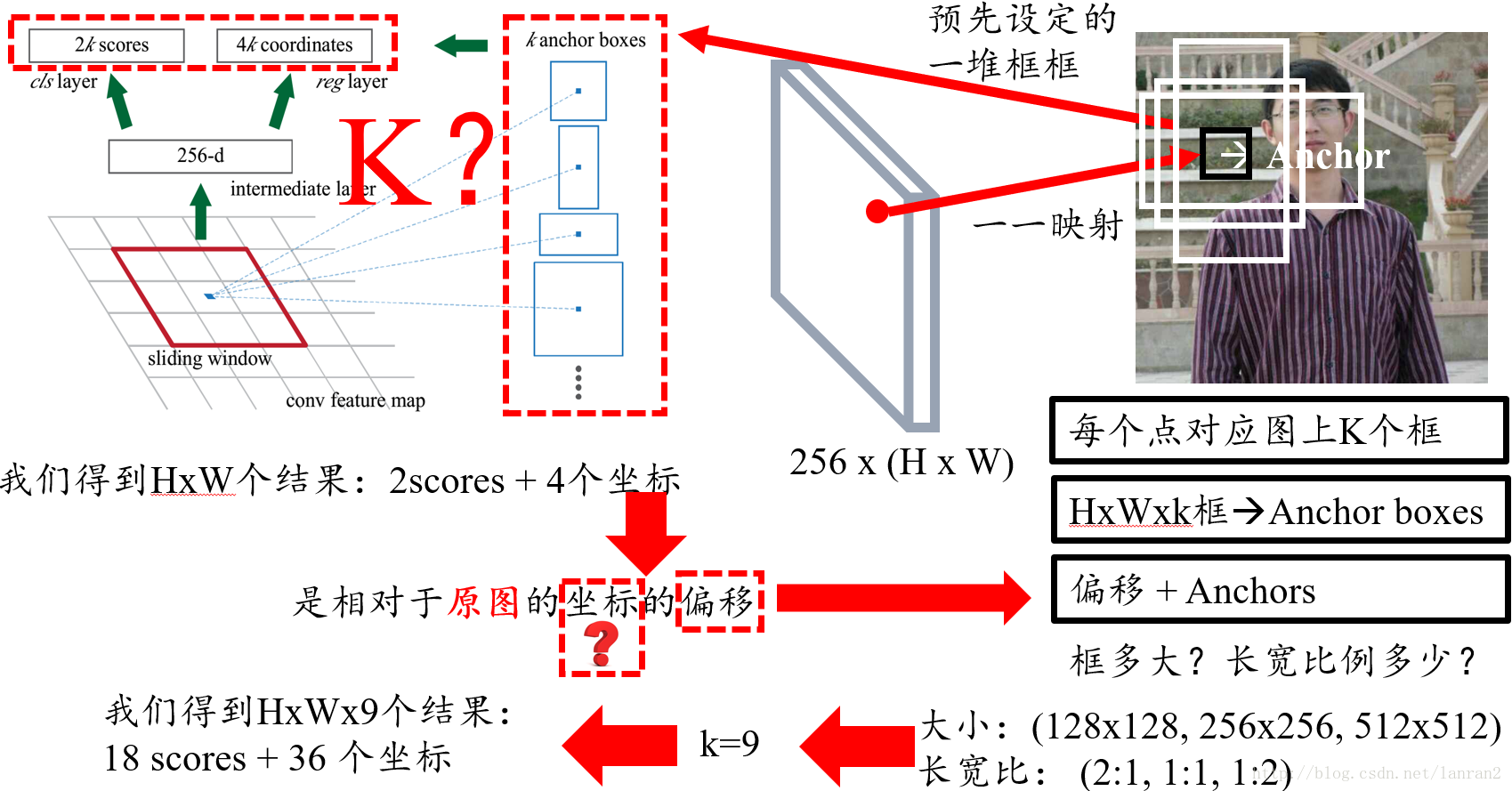 
图4 问题4，5的解答描述图
3. RPN的整个流程回顾
最后我们再把RPN整个流程走一遍，首先通过一系列卷积得到公共特征图，假设他的大小是N x 16 x 16，然后我们进入RPN阶段，首先经过一个3 x 3的卷积，得到一个256 x 16 x 16的特征图，也可以看作16 x 16个256维特征向量，然后经过两次1 x 1的卷积，分别得到一个18 x 16 x 16的特征图，和一个36 x 16 x 16的特征图，也就是16 x 16 x 9个结果，每个结果包含2个分数和4个坐标，再结合预先定义的Anchors，经过后处理，就得到候选框；整个流程如图5：
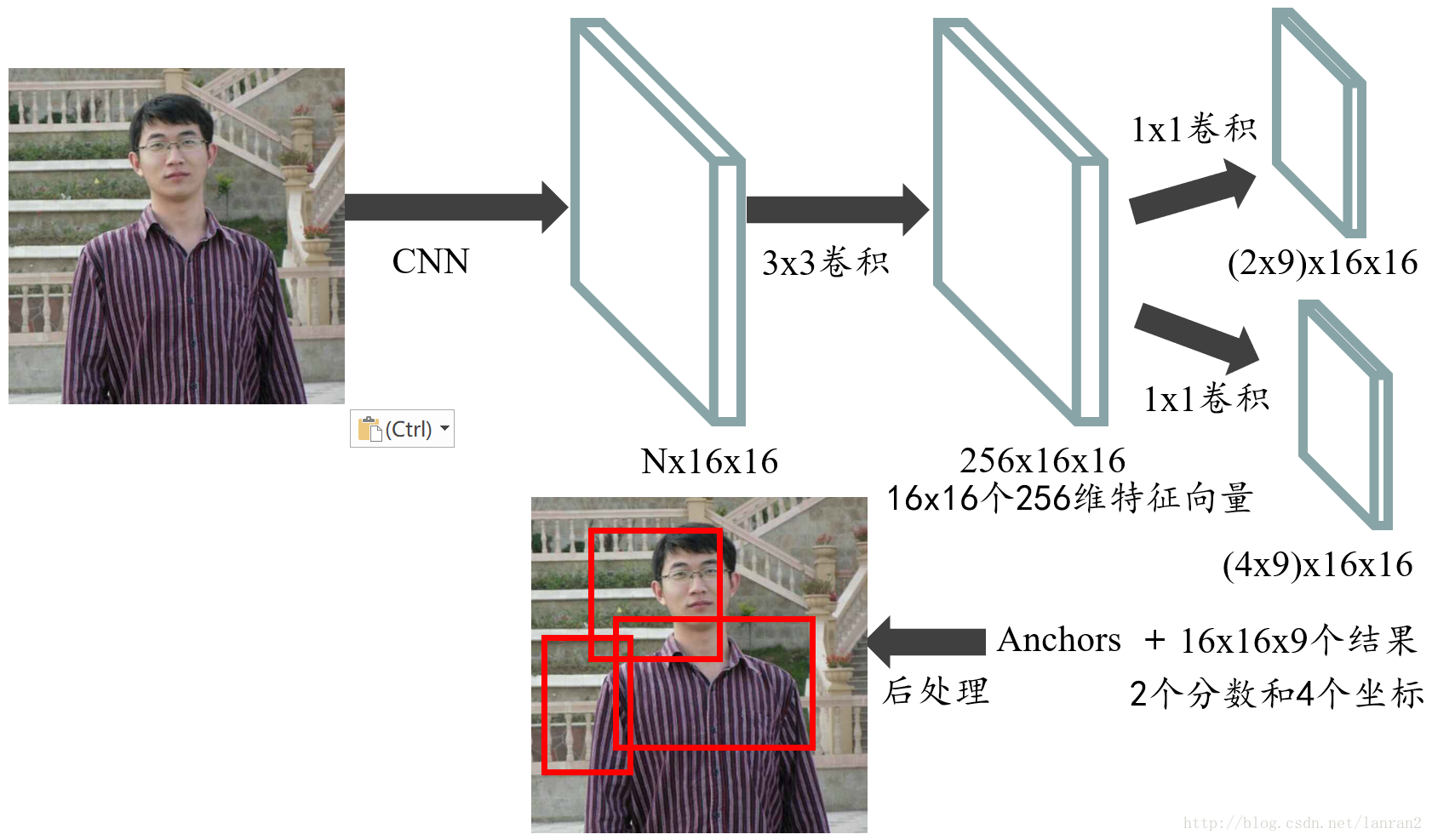图5 RPN整个流程
