TensorFlow实现卷积神经网络
1 卷积神经网络简介
在介绍卷积神经网络(CNN)之前,我们需要了解全连接神经网络与卷积神经网络的区别,下面先看一下两者的结构,如下所示:
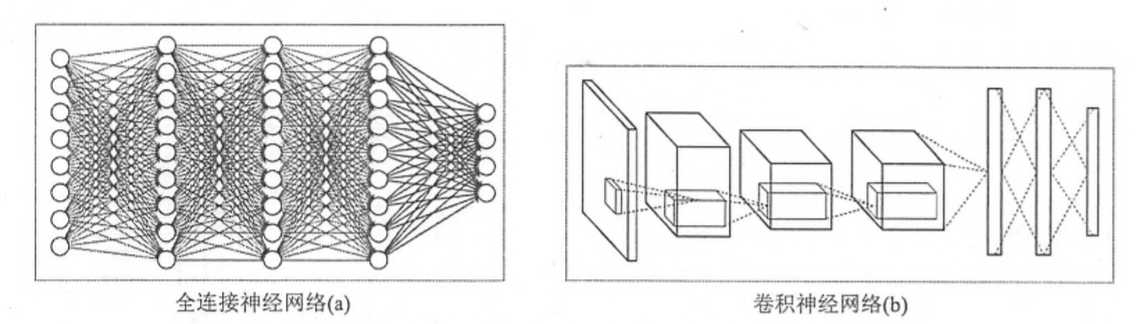
图1 全连接神经网络与卷积神经网络结构
虽然上图中显示的全连接神经网络结构和卷积神经网络的结构直观上差异比较大,但实际上它们的整体架构是非常相似的。从上图中可以看出,卷积神经网络也是通过一层一层的节点组织起来的。和全连接神经网络一样,卷积神经网络中的每一个节点都是一个神经元。在全连接神经网络中,每相邻两层之间的节点都有边相连,于是一般会将每一层全连接层中的节点组织成一列,这样方便显示连接结构。而对于卷积神经网络,相邻两层之间只有部分节点相连,为了展示每一层神经元的维度,一般会将每一层卷积层的节点组织成一个三维矩阵。
在TensorFlow中训练一个卷积神经网络的流程和训练一个全连接神经网络没有任何区别。卷积神经网络和全连接神经网络的唯一区别就在于神经网络中相邻两层的连接方式。在进一步介绍卷积神经网络的连接结构之前,本部分将先介绍为什么全连接神经网络无法很好地处理图像数据。
使用全连接神经网络处理图像的最大问题在于全连接层的参数太多。对于MNIST数据,每一张图片的大小是28×28×1,其中28×28为图片的大小,×1表示图像是黑白的,只有一个色彩通道。假设第一层隐藏层的节点数为500个,那么一个全链接层的神经网络将有28×28×500+500=392500个参数。当图片更大时,比如在Cifar-10数据集中,图片的大小为32×32×3,其中32×32表示图片的大小,×3表示图片是通过红绿蓝三个色彩通道(channel)表示的。这样输入层就有3072个节点,如果第一层全连接层仍然是500个节点,那么这一层全链接神经网络将有3072×500+500~150万个参数。参数增多除了导致计算速度减慢,还很容易导致过拟合问题。所以需要一个更合理的神经网络结构来有效地减少神经网络中参数个数。卷积神经网络就可以达到这个目的。
下边给出一个更加具体用于图像分类的卷积神经网络架构图:
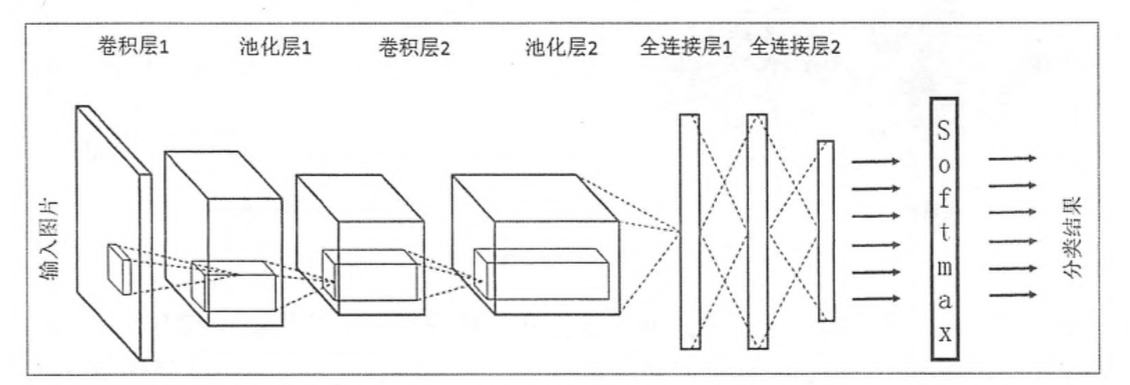
图2:用于图像分类的卷积神经网络架构图
在卷积神经网络的前几层中,每一层的节点都被组织成一个三维矩阵。比如处理Cifar-10数据集中的图片时,可以将输入层组织成一个32×32×3的三维矩阵。上图中虚线部分展示了卷积神经网络的一个连接示意图,从图中可以看出卷积神经网络中前几层中每一个节点只和上一层中部分的节点相连。卷积神经网络的具体连接方式将在下一个部分介绍。
一个卷积神经网络主要由以下5种结构组成:
1.输入层。输入层是整个神经网络的输入,在处理图像的卷积神经网络中,它一般代表了一张图片的像素矩阵。比如在图2中,最左侧的三维矩阵就可以代表一张图片。其中三维矩阵的长和宽代表了图像的大小,而三维矩阵的深度代表了图像的色彩通道(channel)。比如黑白图片的深度为1,而在RGB色彩模式下;图像的深度为3。从输入层开始,卷积神经网络通过不同的神经网络结构将上一层的三维矩阵转化为下一层的三维矩阵,直到最后的全连接层。
2.卷积层。从名字就可以看出,卷积层是一个卷积神经网络中最为重要的部分。和传统全连接层不同,卷积层中每一个节点的输入只是上一层神经网络的一小块,这个小块常用的大小有3×3或者5×5。卷积层试图将神经网络中的每一小块进行更加深入地分析从而得到抽象程度更高的特征。一般来说,通过卷积层处理过的节点矩阵会变得更深,所以在图2中可以看到经过卷积层之后的节点矩阵的深度会增加。
3.池化层(Pooling)。池化层神经网络不会改变三维矩阵的深度,但是它可以缩小矩阵的大小。池化操作可以认为是将一张分辨率较高的图片转化为分辨率较低的图片。通过池化层,可以进一步缩小最后全连接层中节点的个数,从而达到减少整个神经网络中参数的目的。
4.全连接层。如图2所示,在经过多轮卷积层和池化层的处理之后,在卷积神经网络的最后一般会是由1到2个全连接层来给出最后的分类结果。经过几轮卷积层和池化层的处理之后,可以认为图像中的信息已经被抽象成了信息含量更高的特征。我们可以将卷积层和池化层看成自动图像特征提取的过程。在特征提取完成之后,仍然需要使用全连接层来完成分类任务。
5.Softmax层。Softmax层主要用于分类问题。通过Softmax层,可以得到当前样例属于不同种类的概率分布情况。
2 TensorFlow实现卷积神经网络
TensorFlow对卷积神经网络提供了非常好的支持,下面的程序实现了一个卷积层的前向传播过程。从以下代码可以看出,通过TensorFlow实现卷积层是非常方便的。
#通过tf.get variable的方式创建过滤器的权重变量和偏置项变量。上面介绍了卷积层
#的参数个数只和过滤器的尺寸、深度以及当前层节点矩阵的深度有关,所以这里声明的参数变
#量是一个四维矩阵,前面两个维度代表了过滤器的尺寸,第三个维度表示当前层的深度,第四
#个维度表示过滤器的深度。
filter weight =tf.get variable(
'weights',[5,5,3,16],initializer=tf.truncated_normal_initializer(stddev=0.1))
#和卷积层的权重类似,当前层矩阵上不同位置的偏置项也是共享的,所以总共有下一层深度个不
#同的偏置项。本样例代码中16为过滤器的深度,也是神经网络中下一层节点矩阵的深度。
biases=tf.get variable(
'biases',[16],initializer=tf.constant_initializer(0.1))
#tf.nn.conv2d提供了一个非常方便的函数来实现卷积层前向传播的算法。这个函数的第一个输
#入为当前层的节点矩阵。注意这个矩阵是一个四维矩阵,后面三个维度对应一个节点矩阵,第一
#维对应一个输入batch。比如在输入层,input[0,:,:,:]表示第一张图片,input[1,:,:,:]
#表示第二张图片,以此类推。tf.nn.conv2d第二个参数提供了卷积层的权重,第三个参数为不
#同维度上的步长。虽然第三个参数提供的是一个长度为4的数组,但是第一维和最后一维的数字
#要求一定是1。这是因为卷积层的步长只对矩阵的长和宽有效。最后一个参数是填充(padding)
#的方法,TensorFlow中提供SAME或是VALID两种选择。其中SAME表示添加全0填充(如
#图6-11所示),“VALID”表示不添加。
conv=tf.nn.conv2d(
input,filter weight,strides=[1,1,1,1],padding='SAME')
#tf.nn.bias_add提供了一个方便的函数给每一个节点加上偏置项。注意这里不能直接使用加
#法,因为矩阵上不同位置上的节点都需要加上同样的偏置项。
bias=tf.nn.bias_add(conv,biases)
#将计算结果通过ReLU激活函数完成去线性化。
actived conv=tf.nn.relu(bias)
从图2中可以看出,在卷积层之间往往会加上一个池化层,使用最多的是最大值池化(max pooling),tensorflow代码如下:
#tf.nn.max pool实现了最大池化层的前向传播过程,它的参数和tf.nn.conv2d函数类似。
#ksize提供了过滤器的尺寸,strides提供了步长信息,padding 提供了是否使用全0填充。
pool=tf.nn.max pool(actived conv,ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')
注:
(1)卷积神经网络中一般都是一个卷积层后接一个池化层构成一个stage;构建多个这样的结构,然后接上全连接网络(FC)与softmax层,就形成了前向传播的过程。在各个stage中,卷积层units不同。
(2)当你使用TensorFlow构建好前向传播传播过程之后,TensorFlow内部会自动计算好反向传播在在各个节点的微分值,然后配合梯度下降法可以找到使loss最小的点。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号