wqs 二分学习笔记

wqs 二分笔记

目录

• wqs 二分笔记
  • 讲解
    • 模板题题目描述
    • 分析
    • 实现

不得不说这东西理解容易但是写代码的时候一堆边界问题，谔谔

讲解

先放例题：https://www.luogu.com.cn/problem/P5633

模板题题目描述

给你一个有 \(n\) 个节点，\(m\) 条边的带权无向图，你需要求得一个生成树，使边权总和最小，且满足编号为 \(s\) 的节点正好连了 \(k\) 条边。

分析

我们以（生成树中）与编号 \(s\) 相连的边数（\(s\) 的度数）为 \(x\) 轴，生成树的最小边权和为 \(y\) 轴作出函数曲线。

分析可知，此函数可以在中间若干个点达到最小值，这几个点的横坐标都是所有合法的最小生成树中 \(s\) 的度数。

而沿着这最小值点的左方向，函数值会越来越大，而且增速会越来越快。

同理，沿着最小值点的右方向，函数值也越来越大，而且增速会越来越快。

作出图像就是：

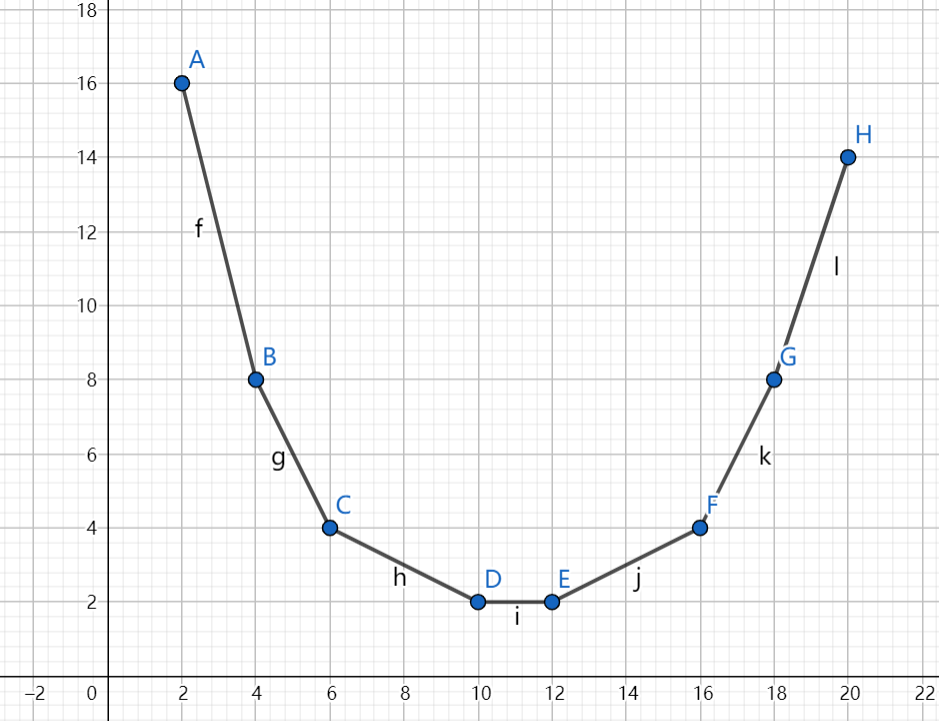
其中 \(D,E\) 就是上文所说的最小值点。

可以发现，作出的函数曲线是一个下凸壳，这意味着随着横坐标的增大，斜率是递增的。

有了递增的性质，我们就可以利用斜率来进行二分了。

比如说，题目要求的 \(s\) 度数为 \(6\)，对应上图的 \(C\) 点，那么通过二分斜率便可以找到一条与 \(C\) 点“相切”的直线：

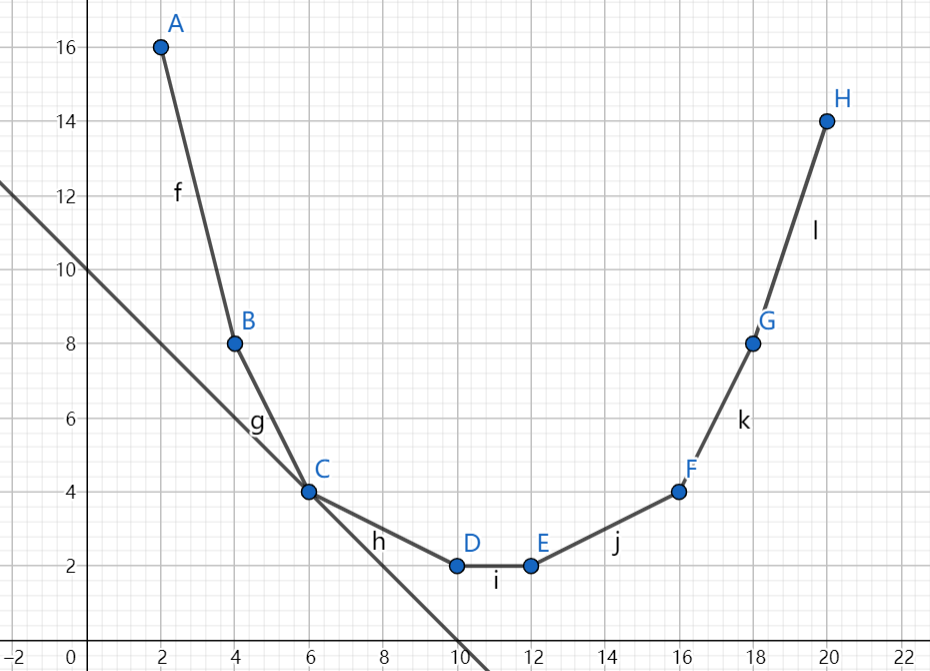
因此，根据函数意义，这个切点 \(C\) 的 \(y\) 轴坐标就是答案了。

从上面的过程就可以发现 wqs 二分的思想了：

因为直接求 \(C\) 的 \(y\) 轴坐标是困难的，所以我们从问题所对应的函数的曲线入手，通过找到的相应的切线的 \(y\) 轴坐标来得到答案。

最后的问题是，怎么找切线呢？

我们就让和 \(s\) 相连的边都减去二分值 \(mid\)，跑一遍最小生成树即可，最小生成树对应的边权和就是上图切线与 \(y\) 轴的截距。而我们要得到切点的 \(y\) 轴坐标就只需要让截距加上 \(cnt \times mid\) 即可，其中 \(cnt\) 就是此最小生成树中 \(s\) 的度数。

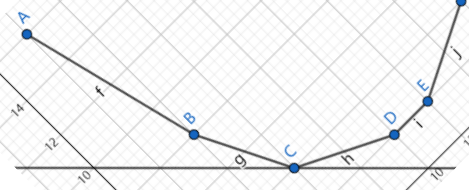
事实上，上面所说的求切点过程可以看作是将曲线进行了旋转，然后找到最小值。（个人认为这样理解最好懂）

而对于其它的题目，我们就根据题目来求相应的最值即可，方法例如：贪心，DP 等。

实现

上面的讲解涉及的细节较少，不妨参考下面的代码进一步理解。

// Problem: P5633 最小度限制生成树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5633
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
#define all(x) (x).begin(), (x).end()

#define x first
#define y second
using pii = pair<int, int>;
using ll = long long;

#define int long long

inline void read(int &x){
    int s=0; x=1;
    char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')x=-1;ch=getchar();}
    while(ch>='0' && ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
    x*=s;
}

const int N=1e5+5, M=1e6+50;

struct Edge{
	int u, v, w;
	
	bool operator < (const Edge &o)const{
		return w<o.w;
	}
}e[M], es[M], buf[M];

int tot, tots, totb;

int f[N];

int find(int x){
	return x==f[x]? x: f[x]=find(f[x]);
}

int n, m, s, k;
int res, cnt;

int cal(int x){
	rep(i,1,tots) es[i].w-=x;
	res=0, totb=0;
	rep(i,1,n) f[i]=i;
	
	for(int i=1, j=1; i<=tots || j<=tot; ){
		if(i>tots || j<=tot && e[j].w<=es[i].w) buf[++totb]=e[j++];
		else buf[++totb]=es[i++];
	}
	
	cnt=0;
	rep(i,1,totb){
		int u=buf[i].u, v=buf[i].v, w=buf[i].w;
		int pu=find(u), pv=find(v);
		if(pu!=pv){
			f[pu]=pv;
			if(u==s || v==s) cnt++;
			res+=w;
		}
	}
	rep(i,1,tots) es[i].w+=x;
	return cnt;
}

bool is_cc(){
	int g=0;
	rep(i,1,n){
		if(!g) g=find(i);
		else if(g!=find(i)) return false; 
	}
	return true;
}

signed main(){
	cin>>n>>m>>s>>k;
	rep(i,1,n) f[i]=i;
	rep(i,1,m){
		int u, v, w; read(u), read(v), read(w);
		if(u==s || v==s) es[++tots]={u, v, w};
		else e[++tot]={u, v, w};
		f[find(u)]=find(v);
	}
	if(!is_cc()) return puts("Impossible"), 0;
	
	sort(es+1, es+1+tots), sort(e+1, e+1+tot);
	
	int l=-30010, r=-l;
	if(cal(r)<k) return puts("Impossible"), 0;
	if(cal(l)>k) return puts("Impossible"), 0;
	
	while(l<r){
		int mid=l+r+1>>1;
		if(cal(mid)<=k) l=mid;
		else r=mid-1;
	}
	cal(l);

	int t=res+l*k;
	cout<<t<<endl;
	
	return 0;
}