【图论】圆方树笔记

基于 yxc 大佬讲解的圆方树的学习笔记。

问题

https://www.acwing.com/problem/content/362/

https://www.acwing.com/problem/content/2866/

https://www.luogu.com.cn/problem/P5236

这三题本质完全一样，是三倍经验。

题意是：给出 $n$ 点 $m$ 边的仙人掌图，对任意两点最短路进行查询。

无向仙人掌图的定义：任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。

比如下面绿色的三个图就是仙人掌，而黑色的不是。特别注意一下两个点如果存在两条不同连边也算（即下图第二个仙人掌）。

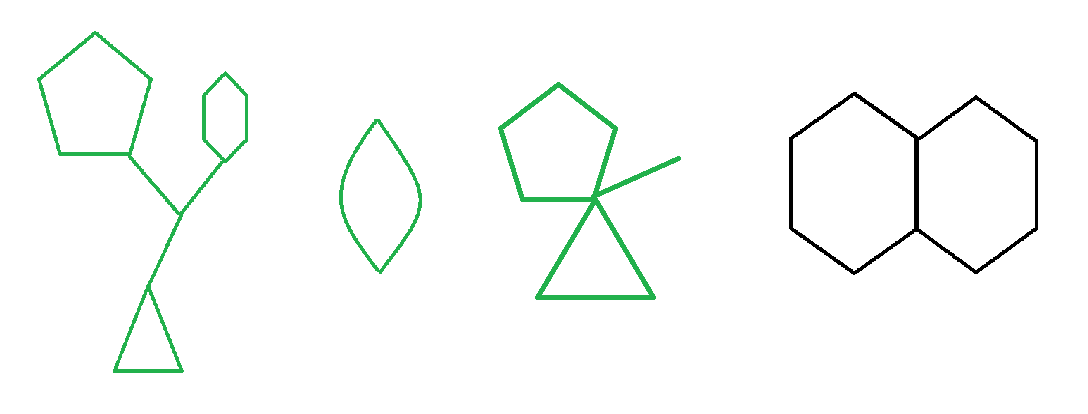
圆方树

因为仙人掌这样的图比较特殊，我们可以比较高效地求出任意两点间的最短路。

这里引入圆方树来解决。

网上很多资料将其作为无向图构建，而 yxc 大佬讲解中当作是外向树构建。在这个问题中两种构建方式不会影响求解，本文将其构建为外向树。

构建

记读入的图为原图，构建的圆方树为新图。

首先，新图保留着原图的点集，这些点记为圆点。

将原图任意一个点（实现中指定 $1$ 号点即可）作为根节点，然后在原图跑一遍 dfs。

每当找到一个环的时候（使用 tarjan 算法维护），将进入环的点（也就是边双的根节点）记为头节点，然后在新图上对加一个方点，并让头节点向这个方点连边，边权为 $0$，同时，方点向其它点 $u$ 连边，边权为原图中的 $u$ 到根节点的最短距离。

下面使原图与对应新图（圆方树）的一个例子：

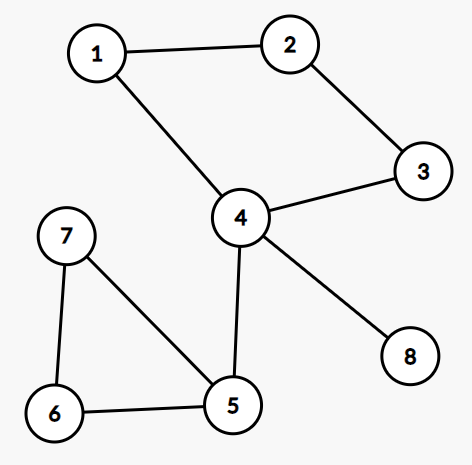
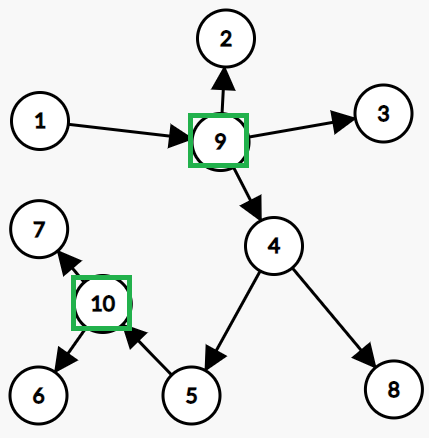
应用

构建完圆方树后，就不难用其来求两点 $u,v$ 最短路了：

• 当两点 $u,v$ 的最近公共祖先（LCA）为圆点时，答案就是圆方树上两点的距离，即：$dis[u, v] = d[u] + d[v] - 2d[lca(u, v)]$。（$d[u]$ 为 $u$ 到根节点的距离）
• 而当两点的 LCA 为方点时，记 $u,v$ 分别与环交于 $U,V$，注意到 $U,V$ 之间的距离有两种，我们需要取其中较短的，记为 $dis(u, v)_{\min}$，那么答案为 $dis(u, v)_{\min} + dis(u, U) + dis(v, V)$。

实现

#include<bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
#define all(x) (x).begin(), (x).end()

#define x first
#define y second
using pii = pair<int, int>;
using ll = long long;

inline void read(int &x){
    int s=0; x=1;
    char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')x=-1;ch=getchar();}
    while(ch>='0' && ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
    x*=s;
}

const int N=2e4+5, M=1e5+5;

int n, m, Q, nwn; // nwn 是圆方树的点数

struct Edge{
	int to, w, next;
}e[M];

int h1[N], h2[N], tot;

void add(int *h, int u, int v, int w){
	e[tot].to=v, e[tot].w=w, e[tot].next=h[u], h[u]=tot++;
}

int scir[N], s[N]; // scir[u] 代表 u 所在的环的边权和，s[u] 代表 u 所在环的前缀和（可以理解为固定一个起点并顺时针/逆时针方向）的长度。
int fu[N], fw[N], fe[N]; // 分别记录 dfs 过程中 dfs 树上 u 点的父节点、u 和父节点的边权，u 和父节点所对应的边的编号。

void build_cir(int x, int y, int W){
	int S=W;
	for(int u=y; u!=x; u=fu[u]){
		s[u]=S;
		S+=fw[u];
	}
	s[x]=scir[x]=S;
	++nwn;
	for(int u=y; u!=x; u=fu[u]){
		scir[u]=S;
		add(h2, nwn, u, min(S-s[u], s[u]));
	}
	add(h2, x, nwn, 0);
}

int dfn[N], low[N], ts;

void dfs(int u, int from){
	dfn[u]=low[u]=++ts;
	for(int i=h1[u]; ~i; i=e[i].next){
		int go=e[i].to;
		if(!dfn[go]){
			fu[go]=u, fw[go]=e[i].w, fe[go]=i;
			dfs(go, i);
			low[u]=min(low[u], low[go]);
			if(dfn[u]<low[go]) add(h2, u, go, e[i].w);
		}
		else if(i!=(from^1)) low[u]=min(low[u], dfn[go]);
	}	
	
	for(int i=h1[u]; ~i; i=e[i].next){ // 把 u 作为边双的根节点所对应的环一一找出来并建立圆方树。
		int go=e[i].to;
		if(dfn[u]<dfn[go] && fe[go]!=i) build_cir(u, go, e[i].w);
	}
}

int fa[N][15], d[N], dep[N];
void get_lca(int u, int p){
	dep[u]=dep[p]+1, fa[u][0]=p;
	rep(i,1,14) fa[u][i]=fa[fa[u][i-1]][i-1];
	for(int i=h2[u]; ~i; i=e[i].next){
		int go=e[i].to;
		d[go]=d[u]+e[i].w;
		get_lca(go, u);
	}
}

int U, V;
int lca(int u, int v){ // 推荐使用倍增法求 lca，因为能够比较方便地找到 lca 的两个儿子
	if(dep[u]<dep[v]) swap(u, v);
	dwn(i,14,0) if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
	if(u==v) return u;
	dwn(i,14,0) if(fa[u][i]!=fa[v][i]) u=fa[u][i], v=fa[v][i];
	U=u, V=v;
	return fa[U][0];
}

int main(){
	memset(h1, -1, sizeof h1);		
	memset(h2, -1, sizeof h2);		
	
	cin>>n>>m>>Q;
	nwn=n;
	rep(i,1,m){
		int u, v, w; read(u), read(v), read(w);
		add(h1, u, v, w), add(h1, v, u, w);
	}
	
	dfs(1, -1);
	get_lca(1, 0);
	while(Q--){
		int u, v; read(u), read(v);
		int p=lca(u, v);
		if(p<=n){
			cout<<d[u]+d[v]-(d[p]<<1)<<endl;
		}
		else{
			int du=d[u]-d[U], dv=d[v]-d[V];
			int t=abs(s[U]-s[V]);
			cout<<(du+dv+min(t, scir[U]-t))<<endl;
		}
	}
	
	return 0;
}