【BCC】冗余路径（做法 + 证明）
题意
给定一个连通的无向图让你进行加边操作，要求每一对点之间都至少有两条相互分离的路径，求最小的加边数。
两条路径相互分离，是指两条路径没有一条重合的道路。
分析
这意味着，从一个点到另一个点，不能够存在一条边满足：如果不经过这条边，这个点就到不了另一个点。
换句话说，就是不能存在一条边，使得去掉这条边后图不连通，那么题目要求的就是：给连通的无向图加边，使得无向图没有桥（即变成边双连通分量），最小化加边数。
做法
因为边双连通分量本来就没有桥，所以我们考虑对整个图求一遍边双连通分量（使用 tarjan 算法），然后将边双连通分量缩为一个点考虑。那么缩完点后得到的图一定是一棵树（因为图中不可能存在环）。
先给出结论：
所加的边数至少为 \(\lceil \frac{cnt}{2} \rceil\) （\(cnt\) 为叶结点个数），而这恰好就是答案。
证明
下面，我们要证明的是：
- 加边数至少为 \(\lceil \frac{cnt}{2} \rceil\)
- 给连通的无向图加 \(\lceil \frac{cnt}{2} \rceil\) （\(cnt\) 为叶结点个数）条边即可保证所得的图为边双连通分量
先证明 1：因为对于一个叶子节点 \(t\) ，如果把它与父节点相连的边割去会让它成为独立点，所以每个叶子节点都需要向其它点连一条边，因此加边数至少为 \(\lceil \frac{cnt}{2} \rceil\) 。
下证 2：
当图的点数 \(V\) 为 \(2\) 时，两个点都是叶节点，结论成立。
考虑 \(V\geqslant 2\) 的情况：
我们一定可以找到一个度数大于 \(1\) 的点，我们将它作为根节点 \(root\) ，直观的构造方法是：
叶子节点取 \(\lfloor \frac{cnt}{2} \rfloor\) 个点与另外 \(\lfloor \frac{cnt}{2} \rfloor\) 个一一相连，如果多出一个点则向根节点连接。
因此，我们只需要考察 \(V\) 为偶数的情况，\(V\) 为奇数时多出来的一个点向根节点连接即可。
但是这个构造方法是要满足一定的约束的，我们要证明在这个约束下仍保证这个构造方法可以实行。下面我们便说明这件事。
根节点下有若干棵子树，设有 \(n\) 棵。
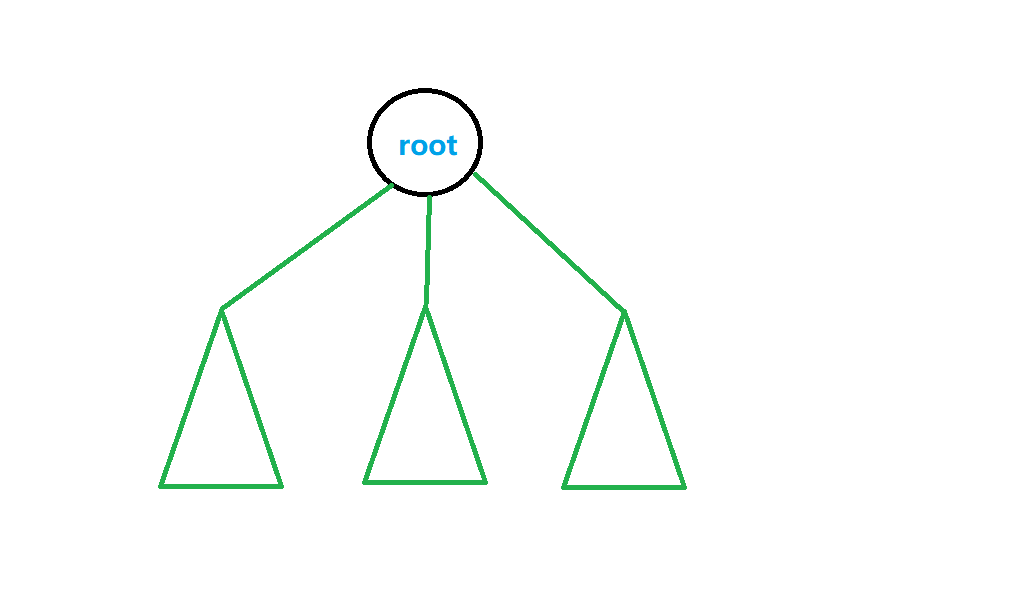
每个子树有若干个叶子节点，个数记为 \(a_1,a_2...a_n\) 。方便起见，我们排好了序（\(a_i \leq a_{i+1}\)）。
所谓约束，就是同一棵子树的叶节点之间不可以相连，因为即便是相连了， \(root\) 与该子树的边依然是桥，如果同一棵子树的叶节点之间存在连边，将次边去掉答案将更优。
下证：不同的子树的叶节点之间连边一定可以得到最优解。
第 \(i,j\) 棵子树间的叶节点连边，等价于 \(a_i,a_j\) 同时减去 \(1\) 。因此连边操作现在等价于：从数列 \(a\) 中选择两个数同时 \(-1\) 。（记为操作）
我们先证明：\(\sum_{i=1}^{n-1} a_i\geq a_n\) 时，一定能通过有限次上述操作使得最后的数列全部为 \(0\)：
构造方法：
将左式 \(a_i\) 的最小值与 \(a_n\) 同时 \(-1\) ，如果左式最小值减为 \(0\) 了就移除，如果出现左式中的 \(a_i > a_n\) 的情况，就将二者调换，继续操作。
最后，我们要证明的是：给出一个 \(V > 2\) 的树，一定存在一个点作为根，使得 子树叶节点树所对应的数列 \(a\) 满足 \(\sum_{i=1}^{n-1} a_i\geq a_n\):
构造方法：任意选取一个度数不为 \(1\) 的点作为根，如果 \(\sum_{i=1}^{n-1} a_i< a_n\) 我们就换根，让 \(a_n\) 所对应的子树的顶点作为根，直到对应的序列满足 \(\sum_{i=1}^{n-1} a_i \geq a_n\) ，这一定是有解的。
证毕。
证明是我乱想出来的，有矛盾的地方请告诉我qwq。
#include<bits/stdc++.h>
using namespace std;
const int N=5005, M=2e4+5;
int n, m;
struct node{
int to, next;
}e[M];
int h[N], tot;
void add(int u, int v){
e[tot].to=v, e[tot].next=h[u], h[u]=tot++;
}
int dfn[N], low[N], ts;
int stk[N], top;
int id[N], bcc_cnt;
bool is_bridge[N];
void tarjan(int u, int from){ // 起始点和从前而来的边
dfn[u]=low[u]=++ts;
stk[++top]=u;
for(int i=h[u]; ~i; i=e[i].next){
int go=e[i].to;
if(!dfn[go]){
tarjan(go, i);
low[u]=min(low[u], low[go]);
if(dfn[u]<low[go]) is_bridge[i]=is_bridge[i^1]=true;
}
else if(i!=(from^1)) // 非反向边
low[u]=min(low[u], dfn[go]);
}
if(dfn[u]==low[u]){
++bcc_cnt;
int y;
do{
y=stk[top--];
id[y]=bcc_cnt;
}while(y!=u);
}
}
int deg[N];
int main(){
memset(h, -1, sizeof h);
cin>>n>>m;
while(m--){
int u, v; cin>>u>>v;
add(u, v), add(v, u);
}
tarjan(1, -1);
for(int i=0; i<tot; i++) if(is_bridge[i]) deg[id[e[i].to]]++;
int cnt=0;
for(int i=1; i<=bcc_cnt; i++) if(deg[i]==1) cnt++;
cout<<(cnt+1)/2<<endl;
return 0;
}
