求n*m网格内矩形的数目
一个n*m的网格,求这个网格中矩形的数目。
比如以下2*2网格,总共有9个矩形:4个1*1的矩形,4个1*2的矩形,1个2*2的矩形
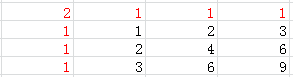
算法1:动态规划,假设dp[i][j]表示以第 i 行第 j 列的格子为右下角顶点的矩形数目,那么dp[i][j] = 1 + dp[i-1][j] + dp[i][j-1] – dp[i-1][j-1] , 这里的1表示i ,j 位置的格子自身构成1*1的矩形,之所以减去dp[i-1][j-1], 因为dp[i-1][j] 和 dp[i][j-1] 都包含了dp[i-1][j-1]。计算时注意i = 1 和 j = 1的边界条件。最后把所有dp[i][j]加起来就是我们所求的答案。以3*3网格举例,为了计算方便,红色为设置的边界值,黑色的才是最后需要加起来的值(结果为36)
int rectNum(int row, int column)
{
vector<vector<int> >dp(row+1, vector<int>(column+1, 1));
int res = 0;
dp[0][0] = 2;
for(int i = 1; i <= row; i++)
for(int j = 1; j <= column; j++)
{
dp[i][j] = 1 + dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1];
res += dp[i][j];
}
return res;
}
算法2:我们假设网格是1行m列的,那么总的矩形数目 = m(1*1的矩形) + m-1(1*2的矩形) + m-2(1*3的矩形) +…+1(1*m的矩形) = m*(m+1)/2,同理n行1列总的矩形数目是n*(n+1)/2. 对于n*m的网格,我们可以先确定好选取的行数(即确定矩形的高),公共有n*(n+1)/2种选法,选好以后就可以压缩成1行m列的网格来考虑了,因此总共n*(n+1)/2*m*(m+1)/2个矩形。(注意最后结果是否溢出int范围) 本文地址
int rectNum(int row, int column)
{
return row*(row+1)*column*(column+1)/4;
}
算法2还可以这样理解:两个对角点就可以确定一个矩形。对于一个n*m的网格,总共有(n+1)*(m+1)个顶点,因此第一个顶点有(n+1)*(m+1)种选取方法,选取好第一个顶点后,第二个顶点就有一些限制了,它不能和第一个顶点在同一条直线上,因此第二个顶点有n*m种选取方法;因此选取两个顶点总共有(n+1)*(m+1)*n*m种选取方法,考虑到矩形ABCD,选取AC、CA、BD、DB都表示同一个矩形,即这些选取方法中,包含的每个矩形都重复了四次,因此总共有(n+1)*(m+1)*n*m/4个矩形。
可以在hduoj 2524上测试算法的正确性
【版权声明】转载请注明出处:http://www.cnblogs.com/TenosDoIt/p/3740141.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号