庞果英雄会第二届在线编程大赛·线上初赛:AB数
给定两个正整数a,b,分别定义两个集合L和R,
集合L:即把1~a,1~b中整数乘积的集合定义为L = {x * y | x,y是整数且1 <= x <=a , 1 <= y <= b};
集合R:1~a,1~b中整数异或的集合定义为集合R = {x ^ y | x,y是整数且1 <= x <=a , 1 <= y <= b},其中^表示异或运算。
现从L中任取一个整数作为A,从R中任取一个整数作为B,如果必要在B的左边补0,使得B达到:“b的位数+1”位(十进制),然后把B接到A的右边,形成的一个十进制数AB。求所有这样形成数的和。
输入a,b 1<=a<=30, 1<=b<=10000000。
输出所有产生的AB数的和,由于结果比较大,输出对1000000007取余数的结果。
例如:a = 2, b = 4,
则L = {1 * 1, 1 * 2, 1 * 3, 1 * 4, 2 * 1, 2 * 2, 2 * 3, 2 * 4} = {1, 2, 3, 4, 6, 8}
R = {1^1,1^2,1^3,1^4,2^1,2^2,2^3,2^4} = {0, 1, 2, 3, 5, 6}
相接的时候保证R中的数至少有两位,所以相接后所有的AB数的集合是
{
100, 101, 102, 103, 105, 106,
200, 201, 202, 203, 205, 206,
300, 301, 302, 303, 305, 306,
400, 401, 402, 403, 405, 406,
600, 601, 602, 603, 605, 606,
800, 801, 802, 803, 805, 806
}
输出它们的和:14502。
假设b的位数为kb, 集合L,R中所有元素的和分别为sumL、sumR,集合L,R中元素的个数分别为sizeL、sizeR。从题目所给的例子可以很容易的分析出最后的结果 = sumL * (10^(kb + 1)) * sizeR + sumR * sizeL (对1000000007求模)。所以我们的目标是求sumL、sizeL和sumR、sizeR。
一 求集合R:sumR、sizeR
我们假设a <= b (如果a > b 可以两者交换),a的十进制位数为ka, b的十进制位数为kb。因此异或求解集合R中元素时,只有b的最后ka个二进制位受影响,b的前kb-ka个二进制位可以表示0…2^(kb-ka)-1的所有数。现在我们只考虑b的后面ka个二进制位:
1、假设b = 11001,a = 101,那么R = {00001…11001}^{001…101}表示的数有哪些呢? 我们可以看到两者异或后可以表示的最大的数是11001^100 = 11101(注意到后三位异或能表示的最大为001^100 = 101), 最小的数是00001^001 = 00000(注意到后三位异或能表示的最小为001^001 = 000),界于最大和最小的数之间的所有数都可以表示(这是因为后三位异或可以表示000~101之间的所有数)。
2、假设b = 11000,a = 101,那么R = {00001…11001}^{001…101}表示的数有哪些呢? 我们可以看到两者异或后可以表示的最大的数是11001^100 = 11101(注意到后三位异或能表示的最大为001^100 = 101), 最小的数是00001^001 = 00000(注意到后三位异或能表示的最小为001^001 = 000),界于最大和最小的数之间的所有数都是不是都可以表示呢,答案是否定的,b本身就不能表示(11000 = 11000^000, 但是题目中说明了y>=1,y不能等于0)。
3、那么什么时候R中不包括b呢:当b的后ka个二进制位全部为0时,b就不属于集合R
4、如何R中的最大元素,要求最大元素,就要使b的后ka个二进制位中1的个数最多,假设a = 10110101, b的后8位为backb = 00101101,注意到我们可以通过异或使backb从左边第三位(左起第一个1)起全部为1(即101101^010010 = 111111),backb的前两位最大能表示00^10 = 10,因此a^backb最大为10111111。即选取b的后ka个二进制位backb,把backb左起第一个二进制位1开始全部置1,backb的其余为和a的对应位异或,这样得到的数就是R的最大值。
5、还需要注意一点是,如果a、b中有一个数为1,那么R中1就不属于集合R,因为1要和0异或才能得到1.
综上所述,我们可以根据步骤4求得R的最大值,那么R = {0,1,2…maxR},然后根据步骤3和步骤5判断一下b和1是否要从R中剔除,求R的复杂度为O(32)(32为整数的位数)
二 求集合L:sumL,sizeL
最简单的就是枚举,用哈希表排除重复元素,但是这样时间复杂度为O(ab), 当b很大时,会超时。
注意到其实我们没有必要求出L中所有的元素,我们需要的是L中元素的个数和元素的和。同理假设a <= b
sumL =
1*{1,2,3…b} +
2*{1,2,3…b} +
…+
a*{1,2,3…b} - 重复的元素
假设集合Li = i * {1,2,3…b}, 注意到为避免重复元素,对于i,不用每次都从1开始乘, 至少可以从 i 开始即 Li = i *{i, i+1,…b}。我们还可以进一步缩小范围,假设i 素因子分解后 i = m * n * k,其中k是最小的素因子,那么我只要从max( b / k +1, i )开始乘,因为m*n*k*(b/k + 1) = m*n*b + i. 当i = m*n 时,m*n*b前面已经计算过,因此至少可以从m*n*b + i 开始计算。所以Li = i * {j, j+1, … ,b}, 其中j = max( b / minPrimeFactor(i) + 1, i ) ( i = 1 时特别考虑)。
所以sumL = U( Li ), 其中(i = 1…a, U表示求集合的并集)。
求集合的并集,我们很容易想到容斥原理:
那么对于集合Lj …Lk的交集可以如下求:
先求j, j+1, …, k 的最小公倍数lcm,那么他们的交集 = lcm * {start…end}, 其中
start = ceil(max( max(b / minPrimeFactor(i) + 1, i ) ) / lcm),i = j…k (即交集的最小元素 >= 所有集合的第一个元素的最大值)
end = j*b / lcm (即交集的最大元素 <= 第一个集合的最大元素)
如果a = 30我们就要求2^30-1次交集,注意到求交集的过程中很多为空集,比如L1∩L2 = 空集,因此L1∩L2∩L3就没必要求了,这样可以减去很多计算。可以通过dfs搜索+剪枝来求sumL,求的过程中我们也很容易求得sizeL。本文地址
三 求最终结果
通过公示 sumL * (10^(kb + 1)) * sizeR + sumR * sizeL (对1000000007求模)求最终结果
最后还需要注意的是,由于数据较大,用int会溢出,(我求最小公倍数时用int,这个错误找了好久)
class Test {
private:
static const long long MAXRES = 1000000007;
static int round(double d)
{
return ceil(d) - d < d - floor(d) ? ceil(d) : floor(d);
}
static long long sequenceSum(int minVal, int maxVal)
{
if(minVal > maxVal)return 0;
return (minVal + maxVal)*(maxVal - minVal + 1LL)/2;
}
//compute Least Common Multiple of a,b
static long long lcm(long long a, long long b)
{
long long tmp, aCopy = a, bCopy = b;
while(b != 0)
{
tmp = b;
b = a % b;
a = tmp;
}
//a is gcd(a,b)
return aCopy / a * bCopy;
}
//compute sum(R) and sizeof(R)
static void computeR()
{
bitset<32> bitMin(minp),bitMax(maxp);
int i = 31;
for(; i >= 0; i--)//find the first bit '1' in minp
if(bitMin[i] == true)break;
int minpBitNum = i + 1;
//containMax indicates whether element max(a,b) is in set R
bool containMax = false;
for(int k = 0; k < minpBitNum; k++)
if(bitMax[k] == true)containMax = true;
for(; i >= 0 && bitMax[i] == false; i--)
bitMax[i] = bitMax[i]^bitMin[i];
for(; i >= 0; i--)
bitMax[i] = true;
int maxR = bitMax.to_ulong();//max element in set R
sumR = 0;//sum of elements in R
sizeR = maxR + 1;//the number of element in R
sumR = sequenceSum(1, maxR);
if(!containMax)
{
sumR = (sumR - maxp) % MAXRES;
if(sumR < 0)sumR += MAXRES;
sizeR--;
}
if(minp == 1)
{
sumR--;
sizeR--;
}
}
static bool computeLRecur(int index, vector<int> &vec, long long lcmVec)
{
if(index == minp + 1)
{
int vecSize = vec.size();
if(vecSize == 0)return true;
int op = vecSize%2 == 0 ? -1 : 1;
int seqStart = 0;
for(int i = 0; i < vecSize; i++)
seqStart = max(seqStart, mulStartVal[vec[i]]);
seqStart = ceil( seqStart * 1.0 / lcmVec );
int seqEnd = vec[0] * maxp / lcmVec;
if(seqStart <= seqEnd)
{
sumL = (sumL + op * lcmVec *sequenceSum(seqStart, seqEnd))
% MAXRES ;
sizeL += op * (seqEnd - seqStart + 1);
return true;
}
else
return false;
}
if(computeLRecur(index + 1, vec, lcmVec))
{
vec.push_back(index);
computeLRecur(index + 1, vec, lcm(lcmVec, index));
vec.pop_back();
return true;
}
else return false;
}
//compute sum(L) and sizeof(L)
static void computeL()
{
//min prime factor of [0,1,2...30]
int minPriFac[] = {0, 1,2,3,2,5,2,7,2,3,2, 11,2,13,2,3,2,17,2,19,2
,3,2,23,2,5,2,3,2,29,2};
sumL = 0;
sizeL = 0;
mulStartVal.clear();
mulStartVal.push_back(0);
mulStartVal.push_back(1);
for(int i = 2; i <= minp; i++)
mulStartVal.push_back(max(maxp / minPriFac[i] + 1, i) * i);
vector<int> vec;
computeLRecur(1, vec, 1);
}
public:
static int minp, maxp;//minp = min(a,b),maxp = max(a,b)
//sumR = sum of elelment in set R
//sumL = sum of elelment in set L
//sizeR = number of element in set R
//sizeL = number of element in set L
static long long sumR, sizeR, sizeL, sumL;
static vector<int> mulStartVal;
static int run (int a,int b)
{
//--------compute the digit number of b
int bDigitNum = 0;
for(int bcopy = b, factor = 10; bcopy != 0;)
{
bcopy = bcopy / factor;
bDigitNum++;
}
minp = a > b ? b : a;
maxp = a > b ? a : b;
//--------comput sum(R) and sizeof(R)
computeR();
//--------comput sum(L) and sizeof(L)
computeL();
//compute final result, result = sumL*factor*sizeR + sumR*sizeL
long long factor = round(pow(10.0, bDigitNum + 1));
long long res = sumL * factor % MAXRES;
res = res * sizeR % MAXRES;
res = (res + (sizeL * sumR)) % MAXRES;
return res;
}
};
int Test::minp;
int Test::maxp;
long long Test::sumL;
long long Test::sizeL;
long long Test::sizeR;
long long Test::sumR;
vector<int> Test::mulStartVal;
//------------------------------------------
int main()
{
int a = 30, b = 10000000;
cout<<Test::run(a,b)<<endl;
return 0;
}
顺便附上caopengcs大神的代码,感谢他的分享

1 const int M = 1000000007; 2 3 int NUM,SUM; 4 int num[22],sum[22],all[33]; 5 6 7 8 class Test3 { 9 public: 10 static int length(int x) { 11 int i; 12 for (i = 0; x; x /=10, ++i) 13 ; 14 return i; 15 } 16 17 static long long gcd(long long x,long long y) { 18 return y?gcd(y, x % y):x; 19 } 20 21 static int mul(long long x, long long y) { 22 if (x >= M) { 23 x %= M; 24 } 25 if (y >= M) { 26 y %= M; 27 } 28 if( (x *= y) >= M) { 29 x %= M; 30 } 31 return x; 32 } 33 34 static int add(long long x,long long y) { 35 if (x >= M) { 36 x %= M; 37 } 38 if (y >= M) { 39 y %= M; 40 } 41 42 if ((x += y) >= M) { 43 x -= M; 44 } 45 return (int) x; 46 } 47 48 static int dec(long long x,long long y) { 49 if (x >= M) { 50 x %= M; 51 } 52 if (y >= M) { 53 y %= M; 54 } 55 if ((x -= y) < 0) { 56 x += M; 57 } 58 return (int) x; 59 } 60 61 static void help(long long x, int one,int *a,int now,int len, long long lcm) { 62 63 if (now >= len) { 64 if (one == 0) { 65 return; 66 } 67 long long n = x / lcm; 68 int s; 69 if (n & 1) { 70 s = mul(n, (n + 1) >> 1); 71 } 72 else { 73 s = mul(n >> 1, n + 1); 74 } 75 s = mul(s, lcm); 76 if (one & 1) { 77 SUM = add(SUM, s); 78 NUM = add(NUM, n); 79 } 80 else { 81 SUM = dec(SUM, s); 82 NUM = dec(NUM, n); 83 } 84 return; 85 } 86 help(x, one, a, now + 1, len, lcm); 87 long long temp = a[now] / gcd(lcm, a[now]); 88 if (temp > x / lcm) { 89 return; 90 } 91 lcm *= temp; 92 help(x, one + 1, a, now + 1, len, lcm); 93 } 94 95 static int run(int a,int b) { 96 int lenb = length(b), lena = length(a), len, L = 0; 97 memset(num,0,sizeof(num)); 98 memset(sum,0,sizeof(sum)); 99 for (int i = 1; i <= a; ++i) { 100 if ((i != 1) && ((i ^ 1) <= b)) { 101 num[0] = add(num[0], 1); 102 sum[0] = add(sum[0], 1); 103 break; 104 } 105 } 106 if (b > 1) { 107 for (int i = 1; i <= a; ++i) { 108 if ((i != b) && ((i ^ b) <= b)) { 109 num[0] = add(num[0], 1); 110 sum[0] = add(sum[0], b); 111 break; 112 } 113 } 114 } 115 for (int i = 2; i < b; ++i) { 116 num[0] = add(num[0], 1); 117 sum[0] = add(sum[0], i); 118 } 119 num[0] = add(num[0], 1); //0 120 for (int i = 1; i <= a; ++i) { 121 for (int j = 1; j <= a; ++j) { 122 if ((((i + b) ^ j) <= b) && (i + b != j)) { 123 len = max(length(i + b) - lenb - 1, 0); 124 num[len] = add(num[len], 1); 125 sum[len] = add(sum[len], i + b); 126 L = max(L, len); 127 break; 128 } 129 } 130 } 131 132 int s = 0, n = 0; 133 // ( (i - 1) * B, i * B] 134 int m = 0; 135 for (int i = a; i; --i) { 136 int k = 0; 137 for (int j = 0; j < m; ++j) { 138 if (all[j] % i) { 139 all[k++] = all[j]; 140 } 141 } 142 all[k++] = i; 143 m = k; 144 long long x = ((long long) i) * ((long long) b); 145 SUM = NUM = 0; 146 help(x, 0, all, 0, m, 1); 147 s = add(s, SUM); 148 n = add(n, NUM); 149 SUM = NUM = 0; 150 help(x - b, 0, all, 0, m, 1); 151 s = dec(s, SUM); 152 n = dec(n, NUM); 153 } 154 int w = 1; 155 for (int i = 0; i <= lenb; ++i) { 156 w = mul(w, 10); 157 } 158 int answer = 0; 159 int numR = 0; 160 161 for (int i = 0; i <= L; ++i) { 162 //printf("%d %d\n",num[i], sum[i]); 163 164 answer = add(add(mul(mul(s, w), num[i]), mul(n, sum[i])), answer); 165 numR += num[i]; 166 } 167 //cout<<"L: "<<s<<" "<<n<<endl; 168 //cout<<"R: "<<numR<<endl; 169 return answer; 170 } 171 };
【版权声明】转载请注明出处:http://www.cnblogs.com/TenosDoIt/p/3496453.html


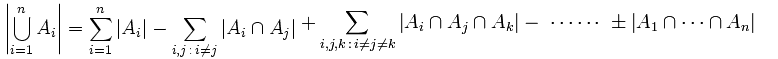


 浙公网安备 33010602011771号
浙公网安备 33010602011771号