(四)栈和队列

上一篇:(三)线性表

1,栈

  1.1顺序栈

  1.2链式栈

  1.3栈的应用

2,队列

  2.1顺序队列

    2.11顺序队列

    2.12循环队列

  2.2链式队列

    2.21链式队列

栈和队列

栈和队列都是受限的线性表，栈只能从一端进出，队列只能一端进一端出

栈

栈有两个端，表尾端称为栈顶(top),表头端称为栈底(bottom),不含元素的空表称为空栈

原则：后进先出

顺序栈

利用顺序存储结构实现栈，这指针top表示栈顶元素在顺序栈中的位置，设base表示栈底元素的位置

实现

//顺序栈
//初始化后，base始终指向栈底，若base==NULL，表明栈结构不存在。top初始
//指向栈底，表明空栈，每当有元素入栈时top++，出栈时top--
#include<iostream>
using namespace std;
#define maxsize 3

class OrderedStack{//==顺序栈存储结构==
public:
    int *base;//栈底
    int *top;//栈顶
    int stacksize;//栈可用容量
    OrderedStack(){};
    ~OrderedStack(){};
};

void initStack(OrderedStack &S){
    S.base=new int[maxsize];
    if(!S.base){
        cout<<"存储空间分配失败"<<endl;
        return;
    }
    S.top=S.base;//top初始化为base，空栈
    S.stacksize=maxsize;
}

void Push(OrderedStack &S,int e){//==入栈==
    if(S.top-S.base==S.stacksize){
        cout<<"栈空间已满"<<endl;
        return;
    }
    *S.top=e;
    S.top++;
}

void Pop(OrderedStack &S,int &e){//==出栈==
    if(S.top==S.base){
        cout<<"栈空"<<endl;
        return;
    }
    S.top--;
    e=*S.top;
}

void getTop(OrderedStack &S){//==获取栈顶元素==
    if(S.top==S.base){
        cout<<"栈空"<<endl;
        return;
    }
    cout<<"栈顶元素为"<<*(S.top-1)<<endl;
}

void isEmpty(OrderedStack &S){//==判空==
    if(S.top==S.base){
        cout<<"栈空"<<endl;
    }else{
        cout<<"栈非空"<<endl;
    }
}

void printStack(OrderedStack &S){//==输出栈==
    int *p=S.top;
    cout<<"输出栈"<<endl;
    while(!(p==S.base)){
        cout<<"|"<<*(p-1)<<"|"<<endl;
        p--;
    }
}

int main(){
  OrderedStack S;
  initStack(S);
  Push(S,12);
  Push(S,13);
  Push(S,9);
  printStack(S);
}

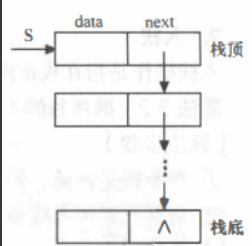
链式栈

定义链式栈的存储结构，包括数据data和指针next；当有新元素入栈时，将新元素的next指针指向前一个元素的地址，首元素的data域不存信息

实现

//链式栈
#include<iostream>
using namespace std;

class LinkedStack{//==链式栈存储结构==
public:
    int data;
    LinkedStack *next;
    LinkedStack(){};
    ~LinkedStack(){};
};
typedef LinkedStack * Linkpoint;

void initStack(Linkpoint &S){//==初始化==
    S=NULL;
}

void Push(Linkpoint &S,int e){//==入栈==
    Linkpoint p=(Linkpoint)malloc(sizeof(LinkedStack));
    p->data=e;
    p->next=S;
    S=p;
}

void Pop(Linkpoint &S,int &e){
    if(S==NULL){
        cout<<"栈空"<<endl;
        return;
    }
    e=S->data;
    Linkpoint p=S;//用p临时保存栈顶元素空间
    S=S->next;
    delete p;//修改完后释放空间，提高空间利用率
}

void getElem(Linkpoint &S){
    if(S==NULL){
        cout<<"栈空"<<endl;
        return;
    }
    cout<<"栈顶元素为:"<<S->data<<endl;
}

void printStack(Linkpoint &S){
    Linkpoint p=S;
    while (p){
        cout<<p->data<<endl;
        p=p->next;
    }
    delete p;
}

int main(){
    Linkpoint S;
    initStack(S);
    Push(S,12);
    Push(S,43);
    Push(S,123);
    printStack(S);
}

栈的应用

经典算法：计算表达式的值

1.初始化两个栈，操作数栈和运算符栈

2.若扫描到操作数，压入操作数栈

3.若扫描到运算符或界限符(主要是"()")，则比对运算符栈顶与扫描到的运算符或界限符的优先级，如果栈顶符号的优先级大于扫描的，则弹出运算符栈，操作数栈弹出两个值，按照弹出的运算符进行运算后自此压入操作数栈。

4.扫描到字符结尾，将操作数栈顶元素弹出就是结果

工具：c++stack库

stack<T> sx; T为数据类型，sx为变量名，创建栈

函数:

s.empty(); //如果栈为空则返回true, 否则返回false; s.size(); //返回栈中元素的个数 s.top(); //返回栈顶元素, 但不删除该元素 s.pop(); //弹出栈顶元素, 但不返回其值 s.push(x); //将元素压入栈顶

实现

//表达式求值
#include<iostream>
#include<stack>
using namespace std;

stack<char> Schar;//运算符栈
stack<double> Sdouble;//操作数栈

int getIndex(char operat){//==获取运算符对应的索引==
    int index=-1;
    switch(operat){
        case '+':
            index=0;
            break;
        case '-':
            index=1;
            break;
        case '*':
            index=2;
            break;
        case '/':
            index=3;
            break;
        case '(':
            index=4;
            break;
        case ')':
            index=5;
            break;
        case '#':
            index=6;
            break;
        default:
            cout<<"error:非法符号";
            break;
    }
    return index;
}

char getPriority(char operat1,char operat2){
    const char priority[][7]={
        {'>', '>', '<', '<', '<', '>', '>'},
        {'>', '>', '<', '<', '<', '>', '>'},
        {'>', '>', '>', '>', '<', '>', '>'},
        {'>', '>', '>', '>', '<', '>', '>'},
        {'<', '<', '<', '<', '<', '=', '0'},
        {'>', '>', '>', '>', '0', '>', '>'},
        {'<', '<', '<', '<', '<', '0', '='},
    };
    int index1=getIndex(operat1);
    int index2=getIndex(operat2);
    return priority[index1][index2];//这里没有异常处理,当index=-1
}

double calculate(double a,char operat,double b){//==计算a operat b==
    switch(operat){
        case '+':
            return a+b;
        case '-':
            return a-b;
        case '*':
            return a*b;
        case '/':
            return a/b;
        default:
            cout<<"error:非法符号";
            return -1;
    }
}

double getAnswer(){//==求表达式值==
    Schar.push('#');
    int counter=0;
    char c=getchar();
    while(c!='#'||Schar.top()!='#'){//当读完c，两个字符都是#时退出循环，计算完毕
        if(isdigit(c)){//isdiget()判断c是字符还是数字
            if(counter==1){//如果counter为1，表示多位数
                double t=Sdouble.top();//取一位数
                Sdouble.pop();//一位数出栈
                Sdouble.push(t*10+(c-'0'));//入栈多位数
                counter=1;//再置一
            }else{
                Sdouble.push(c-'0');//将一位数入栈
                counter++;
            }
            c=getchar();
        }else{
            counter=0;//counter置零
            switch(getPriority(Schar.top(),c)){
                case '<'://优先级不符合，符号入栈
                    Schar.push(c);
                    c=getchar();
                    break;
                case '='://如果两个符号分别时'('和')'则弹出),先计算括号里优先级低的算式
                    Schar.pop();
                    c=getchar();
                    break;
                case '>'://优先级符合时运算
                    char operat=Schar.top();
                    Schar.pop();//取运算符
                    double a=Sdouble.top();
                    Sdouble.pop();//取操作数1
                    double b=Sdouble.top();
                    Sdouble.pop();//取操作数2
                    Sdouble.push(calculate(b,operat,a));//计算，并入栈
            }
        }
    }
    return Sdouble.top();
}
int main(){
    cout<<"输入表达式(以#结尾)"<<endl;
    while(!Schar.empty())
        Schar.pop();
    while(!Sdouble.empty())//若两个栈初始非空,则将其所有元素出栈
        Sdouble.pop();
    double ans=getAnswer();
    cout<<ans<<endl;
}

队列

顺序队列

普通顺序队列

和顺序栈类似，顺序队列中用front和rear分别指示队列头元素及队列尾元素

初始化队列时令front=rear=0,每当插入新元素时，尾指针rear增1；每当删除队列头元素时，头指针front增1

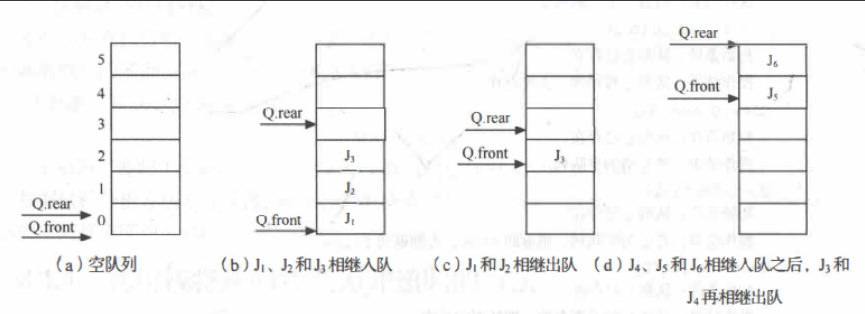
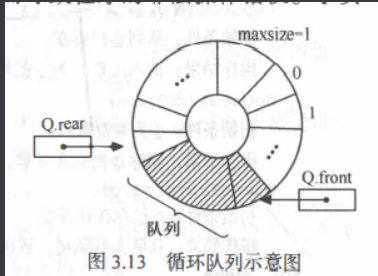
顺序队列在尾指针移动到队尾时，再前进的话会发生溢出错误，但是这时顺序队列并未完全占满如图d，所以引入循环队列，解决此问题

循环队列

实现

//循环队列
/*队列的存储本质还是数组，用base指针存储其首地址，用front,rear计数器来做队
首和队尾指示*/
//通过front=(fornt+1)%maxsize来实现循环
#include<iostream>
using namespace std;
#define maxSize 10
class CircularQueue{//==循环队列存储结构==
    public:
    int *base;//存储空间基址
    int front;//头指针
    int rear;//尾指针
};

void initQueue(CircularQueue &Q){//==初始化==
    Q.base=new int[maxSize];
    if(!Q.base){
        cout<<"空间分配失败"<<endl;
        return;
    }
    Q.front=Q.rear=0;
}

void getLength(CircularQueue &Q){//==求长度==
    cout<<"队列长度为:"<<(Q.rear-Q.front+maxSize)%maxSize<<endl;
}

void Enqueue(CircularQueue &Q,int e){//==入队==
    if((Q.rear+1)%maxSize==Q.front){
        cout<<"队满"<<endl;
        return;
    }
    Q.base[Q.rear]=e;
    Q.rear=(Q.rear+1)%maxSize;
}

void Dequeue(CircularQueue &Q,int &e){//==出队==
    if(Q.front==Q.rear){
        cout<<"队空"<<endl;
        return;
    }
    e=Q.base[Q.front];
    Q.front=(Q.front+1)%maxSize;
}

void getHead(CircularQueue Q){//==取队头元素==
    if(Q.front==Q.rear)
        cout<<"队空"<<endl;
    else
        cout<<"队头元素为"<<Q.base[Q.front]<<endl;
}

void printQueue(CircularQueue Q){//==输出队列==
    if(Q.front==Q.rear){
        cout<<"队空"<<endl;
        return;
    }
    int p=Q.front;
    while (p<Q.rear){
        cout<<Q.base[p]<<endl;
        p++;
    }
}
int main(){
    CircularQueue Q;
    initQueue(Q);
    Enqueue(Q,12);
    Enqueue(Q,32);
    Enqueue(Q,78);
    int e;
    printQueue(Q);
    Dequeue(Q,e);
    getLength(Q);
    printQueue(Q);
    getHead(Q);
}

链式队列

链式队列

实现

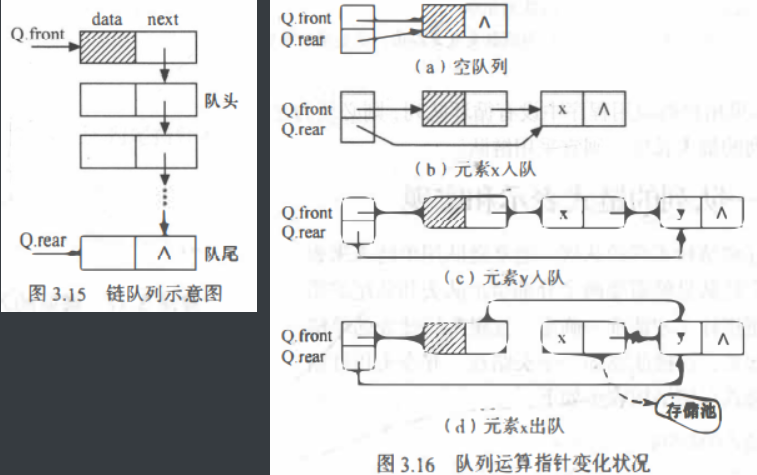
//链式队列
//链式队列的首节点不存数据，用它的指针来指第一个元素
#include<iostream>
using namespace std;

class LinkedQueue{//==节点的存储结构==
    public:
    int data;
    LinkedQueue *next;
};
typedef LinkedQueue * Queueptr;
class LinkQueue{//==指针存储结构==
    public:
    Queueptr front;
    Queueptr rear;
};

void initQueue(LinkQueue &Q){//==初始化==
    Q.front=Q.rear=(Queueptr)malloc(sizeof(LinkedQueue));
    Q.front->next=NULL;
}

void Enqueue(LinkQueue &Q,int e){//==入队==
    Queueptr p=(Queueptr)malloc(sizeof(LinkedQueue));
    p->data=e;
    p->next=NULL;
    Q.rear->next=p;//插到队尾
    Q.rear=p;//更新队尾
}

void Dequeue(LinkQueue &Q,int &e){
    if(Q.front==Q.rear){
        cout<<"队空"<<endl;
        return;
    }
    Queueptr p=Q.front->next;//主要利用队首节点来出队
    e=p->data;
    Q.front->next=p->next;//更新队首节点，就删除了第一个元素
    if(Q.rear==p)
        Q.rear=Q.front;//当最后一个元素被删，队尾指针重新指向头节点
    delete p;
}

void getHead(LinkQueue Q){
    if(Q.front==Q.rear)
        cout<<"栈空"<<endl;
    else
        cout<<"队头元素为:"<<Q.front->next->data<<endl;
}
void printQueue(LinkQueue Q){//==输出==
    if(Q.front==Q.rear){
        cout<<"队空"<<endl;
        return;
    }
    Queueptr p=Q.front->next;
    while (p){
        cout<<p->data<<endl;
        p=p->next;
    }
    
}
int main(){
    LinkQueue Q;
    initQueue(Q);
    Enqueue(Q,12);
    Enqueue(Q,23);
    Enqueue(Q,357);
    int e;
    Dequeue(Q,e);
    printQueue(Q);
    getHead(Q);
}

下一篇:(五)串、数组和广义表