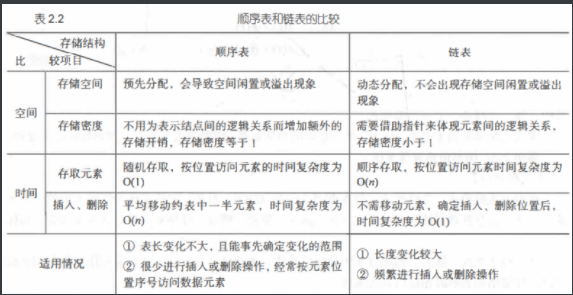
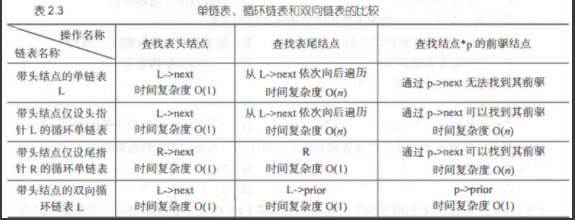
(三)线性表
上一篇:(二)时间复杂度和空间复杂度
1,顺序表
2.链表
3.总结
顺序表
基本操作
InitList (&L) :构造一个空的线性表L。
DestroyList(&L) :销毁线性表L。
ClearList (&L):将L重置为空表。
ListEmpty(L) :若L为空表, 则返回true, 否则返回false。
ListLength(L) :返回L中数据元素个数。
GetElem(L,i,&e) :若,1≤i≤ListLength(L),则用e返回L中第i个数据元素的值。
LocateElem(L,e) :返回L中第1个 值与e相同的元素在 L中的位置 。若这样的数据元素不存在 , 则返回值为0。
PriorElem(r,,cur_e,&pre_e) :若cur_e是L的数据元素,且不是第一个,则用pre_e返回其前驱,否则操作失败,pre_e无定义。
Listinsert(&L,i,e) :若1≤i≤ListLength(L)+1,在 L中第1个位置之前插入新的数据元素 e, L的长度加1。
ListDelete(&L,i) :若1≤i≤ListLength(L),删除L的第1个数据元素,L的长度减1。
TraverseList(L) :对线性表L进行遍历,在遍历过程中对 L的每个结点访问一次。
各操作时间复杂度:
按序查找:O(1):直接取用
按值查找:O(n)(最坏情况,具体看算法)
插入或删除:O(n):每次插入或删除元素都要对后面的所有元素后移或前移,若操作的元素在开头或末尾,则需要操作n次
静态顺序表
长度固定,一旦初始化后不再改变
//静态顺序表
#include<iostream>
using namespace std;
#define maxSize 5//定义最大长度
class StaticOrderList//==静态顺序表存储结构==
{
public:
int * elem;//首地址
int length;//已存入的元素的长度
StaticOrderList();
~StaticOrderList();
};
StaticOrderList::StaticOrderList()
{
}
StaticOrderList::~StaticOrderList()
{
}
bool initList(StaticOrderList &L){//==初始化==
L.elem=new int[maxSize];//静态分配空间
if(!L.elem){
cout<<"存储空间分配失败"<<endl;
return false;
}
L.length=0;
return true;
}
bool getElem(StaticOrderList &L,int i,int &e){//==取值==
if(i<1||i>L.length){
cout<<"取值范围无效"<<endl;
return false;
}
e=L.elem[i-1];
return true;
}
int locateElem(StaticOrderList &L,int e){//==查找==
for (int i = 0; i < L.length; i++)
{
if(L.elem[i]==e){
return i+1;
}
}
cout<<"未查到该元素"<<endl;
return 0;
}
bool listInsert(StaticOrderList &L,int i,int e){//==插入==
if(i<1||i>L.length+1){
cout<<"插入范围无效"<<endl;
return false;
}
if(L.length==maxSize){
cout<<"空间已满"<<endl;
return false;
}
for(int j=L.length-1;j>=i-1;j--){
L.elem[j+1]=L.elem[j];
}
L.elem[i-1]=e;
L.length++;
return true;
}
bool listDelete(StaticOrderList &L,int i){//==删除==
if(i<1||i>L.length){
cout<<"删除范围无效"<<endl;
return false;
}
for(int j=i;j<=L.length-1;j++){
L.elem[j-1]=L.elem[j];
}
L.length--;
return true;
}
void printList(StaticOrderList &L){
cout<<"输出表:";
for(int i=0;i<=L.length-1;i++){
cout<<L.elem[i]<<" ";
}
cout<<endl;
}
int main(){
StaticOrderList L;
initList(L);
listInsert(L,1,2);
listInsert(L,1,4);
listInsert(L,1,6);
listInsert(L,1,3);
listInsert(L,2,7);
printList(L);
listDelete(L,2);
printList(L);
cout<<L.length;
}动态顺序表
//动态顺序表
#include<iostream>
using namespace std;
#define initSize 3
class DynamicOrderList
{
public:
int *elem;
int length;
int maxSize;
DynamicOrderList(){};
~DynamicOrderList(){};
};
bool initList(DynamicOrderList &L){//==初始化==
L.elem=(int *)malloc(initSize * sizeof(int));
if(!L.elem){
cout<<"存储空间分配失败"<<endl;
return false;
}
L.length=0;
L.maxSize=initSize;
return true;
}
void increaseSize(DynamicOrderList &L,int len){//动态增加长度
int *p=L.elem;
L.elem=new int[L.maxSize + len];
for(int i=0;i<L.length;i++){
L.elem[i]=p[i];
}
L.maxSize+=len;
delete p;
}
bool getElem(DynamicOrderList &L,int i,int &e){//==取值==
if(i<1||i>L.length){
cout<<"取值范围无效"<<endl;
return false;
}
e=L.elem[i-1];
return true;
}
int locateElem(DynamicOrderList &L,int e){//==查找==
for (int i = 0; i < L.length; i++)
{
if(L.elem[i]==e){
return i+1;
}
}
cout<<"未查到该元素"<<endl;
return 0;
}
bool listInsert(DynamicOrderList &L,int i,int e){//==插入==
if(i<1||i>L.length+1){
cout<<"插入范围无效"<<endl;
return false;
}
if(L.length==L.maxSize){
increaseSize(L,2);//空间满了之后再申请
}
for(int j=L.length-1;j>=i-1;j--){
L.elem[j+1]=L.elem[j];
}
L.elem[i-1]=e;
L.length++;
return true;
}
bool listDelete(DynamicOrderList &L,int i){//==删除==
if(i<1||i>L.length){
cout<<"删除范围无效"<<endl;
return false;
}
for(int j=i;j<=L.length-1;j++){
L.elem[j-1]=L.elem[j];
}
L.length--;
return true;
}
void printList(DynamicOrderList &L){
cout<<"输出表:";
for(int i=0;i<=L.length-1;i++){
cout<<L.elem[i]<<" ";
}
cout<<endl;
}
int main(){
DynamicOrderList L;
initList(L);
listInsert(L,1,2);
listInsert(L,1,3);
listInsert(L,2,7);
printList(L);
cout<<L.maxSize;
listInsert(L,2,5);
printList(L);
cout<<L.maxSize;
}链表
在物理存储单元上非连续,非顺序的存储结构
根据链表结点所含指针个数、指针指向和指针连接方式,可将链表分为单链表、循环链表、 双向链表、二叉链表、十字链表、邻接表、邻接多重表等。
其中单链表、循环链表和双向链表用 千实现线性表的链式存储结构,其他形式多用于实现树和图等非线性结构。
单链表
普通单链表

带头节点的单链表

几个概念:
首元节点:链表中第一个数据的节点,普通单链表的第一个,带头结点的单链表的第二个
头节点:首元节点前设置的节点,其指针域指向首元节点,数据域可以不存储任何信息,也可以存储单链表的附加信息
头指针:链表的首地址,若无头节点,指向第一个数据,若有,指向第一个元素
增加头节点
1.增加头节点,对链表的第一个元素的操作与其他元素相同,无需特殊处理
2.无头节点的链表判空条件:L==NULL;有头节点的链表判空条件:L->next==NULL
带头节点的单链表的实现
//有头节点的单链表
/*ps:开始用的对象和指针,后来发现函数中实例化的对象是局部变量,返回出来的L
只能记录相邻的数据,之后的数据随函数释放而消失,所以改用malloc分配空间,对
地址的操作是可以记录的*/
#include<iostream>
using namespace std;
class SingleLinkedList{//==单链表的存储结构==
public:
int data;
SingleLinkedList *nextp;
SingleLinkedList(){};
~SingleLinkedList(){};
};
typedef SingleLinkedList * Linkpoint;
void initList(Linkpoint &L){//==初始化==
L=(Linkpoint)malloc(sizeof(SingleLinkedList));
L->data=0;//头节点的data域存单链表的长度
L->nextp=NULL;//nextp域存下一个节点地址
}
void listInsert(Linkpoint &L,int i,int e){//插入
Linkpoint p=L;//在函数内对L操作都用新的指针,不要直接对L操作
Linkpoint s=(Linkpoint)malloc(sizeof(SingleLinkedList));
int j=1;
while(p&&(j<i)){
p=p->nextp;
j++;
}
if(!p||j>i){
cout<<"插入范围无效"<<endl;
return;
}
s->data=e;
s->nextp=p->nextp;
p->nextp=s;
L->data++;
}
void printList(Linkpoint &L){//==输出==
Linkpoint p=L->nextp;
cout<<"输出单链表"<<endl;
while(p){//因为头节点最初指向NULL,每次插入后,尾节点都指向NULL
cout<<p->data<<"->";
p=p->nextp;
}
cout<<"NULL"<<endl;
cout<<"单链表的长度为:"<<L->data<<endl;
}
void getElem(Linkpoint &L,int i){//==取值==
Linkpoint p=L->nextp;
int j=1;
while (p&&(j<i)){
p=p->nextp;
j++;
}
if(!p||j>i){
cout<<"取值范围无效"<<endl;
return;
}
cout<<"第"<<i<<"个元素为:"<<p->data<<endl;
}
void locateElem(Linkpoint &L,int e){//==查找==
Linkpoint p=L->nextp;
int j=1;
while(p){
if(p->data==e){
cout<<"元素"<<e<<"在第"<<j<<"位"<<endl;
return;
}
p=p->nextp;
j++;
}
cout<<"待查找元素不存在"<<endl;
}
void deleteElem(Linkpoint &L,int i){//==删除==
Linkpoint p=L;
Linkpoint s=(Linkpoint)malloc(sizeof(SingleLinkedList));
int j=1;
while(p&&(j<i)){
p=p->nextp;
j++;
}
if(!p||j>i){
cout<<"删除范围无效"<<endl;
return;
}
Linkpoint q;
q=p->nextp;
p->nextp=q->nextp;//令p-next指向p-next-next就把p-next删除了
delete q;
L->data--;
}
//建立单链表-头插法和尾插法
void createList_H(Linkpoint &L,int n){//==输入n个字符插入单链表==
L=(Linkpoint)malloc(sizeof(SingleLinkedList));
L->nextp=NULL;
L->data=0;//L.data存长度
cout<<"输入数据按回车继续:";
for(int i=0;i<n;i++){
Linkpoint p=(Linkpoint)malloc(sizeof(SingleLinkedList));
cin>>p->data;
p->nextp=L->nextp;
L->nextp=p;
L->data++;
}
}
void createList_R(Linkpoint &L,int n){//==尾插法==
L=(Linkpoint)malloc(sizeof(SingleLinkedList));
L->nextp=NULL;
L->data=0;
Linkpoint r=L;
for(int i=0;i<n;i++){
Linkpoint p=(Linkpoint)malloc(sizeof(SingleLinkedList));
cin>>p->data;
p->nextp=NULL;
r->nextp=p;
r=p;
L->data++;
}
}
int main(){
Linkpoint L;
createList_R(L,5);
printList(L);
}循环链表
循环链表就是一种特殊的单链表,其尾节点的指针指向了头节点,使节点首尾相连
单链表:p=NULL或p->next=NULL
循环链表:p=L或p->next=NULL
双向链表
循环单链表中查找后继节点的执行时间为O(1),而查找其前驱节点的时间为O(n),因为只能顺指针方向像狗查询,双向链表加上前驱指针后解决了这个问题
双向链表和单链表的区别就是双链表有前后两个指针,分别指向其前驱和后继
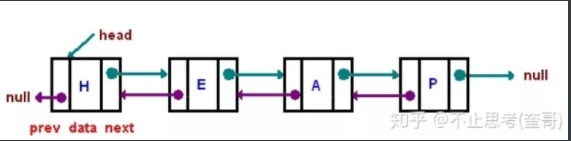
对于双链表,有d->next->prior=d->prior->next=d
实现
因为初始化的节点也可以存数据,所以加入flag标志是否初始节点
此双链表的结构是可以随意插入删除,L始终是首节点的地址,输出是从L开始向后输出的
且首节点的len记录链表长度,当L地址发生变化时,确保新L的len还能记录长度
L地址变化的情况:首节点前插入,删除首节点
//双链表
//本程序的初始节点不是头节点,只是初始化后的第一个点
//开始用p.next==NULL&&p.prior==NULL来判断初始节点,然后对其data域操作,
//但是操作后,L的next和prior还是null的,所以增加flag来标志初始节点
#include<iostream>
using namespace std;
class DoubleLinkedList{//==双链表存储结构==
public:
int data;
int flag=0;//flag标志节点是否初始节点,默认不是初始节点
int len;
DoubleLinkedList * prior;
DoubleLinkedList * next;
DoubleLinkedList(){};
~DoubleLinkedList(){};
};
typedef DoubleLinkedList * DuLinkList;
void initList(DuLinkList &L){//==初始化==
L=(DuLinkList)malloc(sizeof(DoubleLinkedList));
L->prior=NULL;
L->next=NULL;
L->flag=1;//初始化
L->len=0;//len记录链表长度
}
void listInsert_H(DuLinkList &L,int i,int e){//==前插==
if(L->flag){//如果是初始节点,把第一个数据插在其data域
L->data=e;
L->flag=0;//之后标志位置零
L->len++;//长度+1
return;
}
int j=1;
int len=L->len;//记录旧长度
DuLinkList p=L;
while(p&&(j<i)){//p移动到待插位置
p=p->next;
j++;
}
if(!p||j>i){
cout<<"插入范围无效"<<endl;
return;
}
DuLinkList s=(DuLinkList)malloc(sizeof(DoubleLinkedList));
s->data=e;
s->prior=p->prior;
if(p->prior){
p->prior->next=s;//p的前驱的后继本来是p,现在是前插的s;(这里,
} //若p是初始节点,则其没有前驱和后继节点)
s->next=p; //严蔚敏的教材上没有这一步的判断,导致NULL无
p->prior=s; //指针程序错误
if(i==1){//如果,插在第一个元素前面,则更新L,使L始终为开头
L=s;
}
L->len=len+1;//记录新长度
}
void listInsert_R(DuLinkList &L,int i,int e){//==后插==
if(L->flag){
L->data=e;
L->flag=0;
L->len++;
return;
}
int j=1;
int len=L->len;//记录旧长度
DuLinkList p=L;
while(p&&(j<i)){
p=p->next;
j++;
}
if(!p||j>i){
cout<<"插入范围无效"<<endl;
return;
}
DuLinkList s=(DuLinkList)malloc(sizeof(DoubleLinkedList));
s->data=e;
s->next=p->next;
if(p->next){//同前插,若后继为NULL,则跳过,否则更新
p->next->prior=s;
}
s->prior=p;
p->next=s;
L->len=len+1;
}
void printList(DuLinkList &L){//==输出==
if(L->flag){
cout<<"NULL<->NULL"<<endl;
cout<<"链表长度为:0"<<endl;
return;
}
DuLinkList p=L;
cout<<"输出双链表"<<endl;
cout<<"NULL<->";
while(p){//因为头节点最初指向NULL,每次插入后,尾节点都指向NULL
cout<<p->data<<"<->";
p=p->next;
}
cout<<"NULL"<<endl;
cout<<"链表长度为:"<<L->len<<endl;
}
void deleteElem(DuLinkList &L,int i){//==删除==
int j=1;
int len=L->len;//记录旧长度
DuLinkList p=L;
while(p&&(j<i)){
p=p->next;
j++;
}
if(!p||j>i){
cout<<"删除范围无效"<<endl;
return;
}
if(!(p->prior||p->next)){//分情况:初始节点
L->flag=1;//初始节点,flag置1
}else if(!p->prior){//首节点,此时需要更新L
p->next->prior=NULL;
L=p->next;
}else if(!p->next){//尾节点
p->prior->next=NULL;
}else{//中间节点
p->prior->next=p->next;
p->next->prior=p->prior;
}
L->len=len-1;
}
int main(){
DuLinkList L;
initList(L);
listInsert_H(L,1,23);
listInsert_H(L,1,45);
listInsert_H(L,2,12);
deleteElem(L,2);
deleteElem(L,1);
deleteElem(L,1);
printList(L);
}
本文来自博客园,作者:Tenerome,转载请注明原文链接:https://www.cnblogs.com/Tenerome/articles/DataStructure3.html