(五)串，数组和广义表

串

定义

由零个或多个字符组成的有限序列

串中任意个连续的字符组成的子序列称为该串的子串

由一个或多个空格组成的串称为空格串，空格串不是空串

串也有两种存储结构，顺序存储和链式存储，但考虑到存储效率和算法的方便性，串多采用顺序存储结构

串的存储实现不难，但是串的模式匹配很重要

模式匹配算法

子串的定位运算被称为串的模式匹配或串匹配。设有S和T两个字符串，S称为主串，也叫正文串，T称为子串，也叫模式。模式匹配就是在主串S中查找与模式T相匹配的子串，若成功，则返回字串第一个字符在主串中的位置

1.BF算法

//串的顺序存储
//BF算法实现串的模式匹配
//直接使用c++库函数string
#include<iostream>
#include<string>
using namespace std;

void Index_BF(string S,string T){//S主串，T子串
    int i=0,j=0;
    while(i<=S.length()-1&&j<=T.length()-1){
        if(S[i]==T[j]){
            i++;
            j++;
        }else{
            i=i-j+1;//一旦查找不对，i从下一位，j从首位开始重新比较，指针回溯
            j=0;
        }
    }
    if(j>T.length()-1){//退出循环时，如果j达到条件，则匹配到了，i达到条件，则匹配失败
        cout<<"匹配成功"<<endl;
        cout<<"子串在主串的位置是:"<<i-T.length()+1<<endl;
    }else{
        cout<<"匹配失败"<<endl;
    }
}
int main(){
    string str="aaaabcd";
    string ttr="aabcd";
    Index_BF(str,ttr);
}

最坏情况时的时间复杂度O(n*m):主串长度n，子串长度m，相当于两层for循环

2.KMP算法

"KMP"算法相比于"BF"算法，优势在于：

• 在保证指针 i 不回溯的前提下，当匹配失败时，让模式串向右移动最大的距离；
• 并且可以在O(n+m)的时间数量级上完成对串的模式匹配操作； 故，"KMP"算法称为“快速模式匹配算法”。

保证 i 指针不回溯的前提下，如果想实现功能，就只能让 j 指针回溯

j 指针回溯的距离，就相当于模式串向右移动的距离。 j 指针回溯的越多，说明模式串向右移动的距离越长。

对于一个给定的模式串，其中每个字符都有可能会遇到匹配失败，这时对应的 j 指针都需要回溯，具体回溯的位置其实还是由模式串本身来决定的，和主串没有关系

计算next数组:

计算方法是：对于模式串中的某一字符来说，提取它前面的字符串，分别从字符串的两端查看连续相同的字符串的个数，在其基础上 +1 ，结果就是该字符对应的值。

每个模式串的第一个字符对应的值为 0 ，第二个字符对应的值为 1 。

例如：求模式串 “abcabac” 的 next 。前两个字符对应的 0 和 1 是固定的。

对于字符 ‘c’ 来说，提取字符串 “ab” ，‘a’ 和 ‘b’ 不相等，相同的字符串的个数为 0 ，0 + 1 = 1 ，所以 ‘c’ 对应的 next 值为 1 ；

第四个字符 ‘a’ ，提取 “abc” ，从首先 ‘a’ 和 ‘c’ 就不相等，相同的个数为 0 ，0 + 1 = 1 ，所以，‘a’ 对应的 next 值为 1 ；

第五个字符 ‘b’ ，提取 “abca” ，第一个 ‘a’ 和最后一个 ‘a’ 相同，相同个数为 1 ，1 + 1 = 2 ，所以，‘b’ 对应的 next 值为 2 ；

第六个字符 ‘a’ ，提取 “abcab” ，前两个字符 “ab” 和最后两个 “ab” 相同，相同个数为 2 ，2 + 1 = 3 ，所以，‘a’ 对应的 next 值为 3 ；

最后一个字符 ‘c’ ，提取 “abcaba” ，第一个字符 ‘a’ 和最后一个 ‘a’ 相同，相同个数为 1 ，1 + 1 = 2 ，所以 ‘c’ 对应的 next 值为 2 ；

所以，字符串 “abcabac” 对应的 next 数组中的值为（0,1,1,1,2,3,2）。

具体的算法如下：

模式串T为(下标从1开始)：“abcabac” next数组(下标从1开始)： 01

第三个字符 ‘c’ ：由于前一个字符 ‘b’ 的 next 值为 1 ，取 T[1] = ‘a’ 和 ‘b’ 相比较，不相等，继续；由于 next[1] = 0，结束。 ‘c’ 对应的 next 值为1；（只要循环到 next[1] = 0 ,该字符的 next 值都为 1 ）

模式串T为： “abcabac” next数组(下标从1开始)：011

第四个字符 ’a‘ ：由于前一个字符 ‘c’ 的 next 值为 1 ，取 T[1] = ‘a’ 和 ‘c’ 相比较，不相等，继续；由于 next[1] = 0 ，结束。‘a’ 对应的 next 值为 1 ；

模式串T为： “abcabac” next数组(下标从1开始)：0111

第五个字符 ’b’ ：由于前一个字符 ‘a’ 的 next 值为 1 ，取 T[1] = ‘a’ 和 ‘a’ 相比较，相等，结束。 ‘b’ 对应的 next 值为：1(前一个字符 ‘a’ 的 next 值) + 1 = 2 ；

模式串T为： “abcabac” next数组(下标从1开始)：01112

第六个字符 ‘a’ ：由于前一个字符 ‘b’ 的 next 值为 2，取 T[2] = ‘b’ 和 ‘b’ 相比较，相等，所以结束。‘a’ 对应的 next 值为：2 (前一个字符 ‘b’ 的 next 值) + 1 = 3 ；

模式串T为： “abcabac” next数组(下标从1开始)：011123

第七个字符 ‘c’ ：由于前一个字符 ‘a’ 的 next 值为 3 ，取 T[3] = ‘c’ 和 ‘a’ 相比较，不相等，继续；由于 next[3] = 1 ，所以取 T[1] = ‘a’ 和 ‘a’ 比较，相等，结束。‘a’ 对应的 next 值为：1 ( next[3] 的值) + 1 = 2 ；

模式串T为： “abcabac” next数组(下标从1开始)：0111232

基于next的KMP算法的实现

先看一下 KMP 算法运行流程（假设主串：ababcabcacbab，模式串：abcac）。

第一次匹配：

第二次匹配:

第三次匹配:

原理理解:

i指针一直前进，当有子串中的相同元素时，比较其前的元素和子串中相同元素前的元素是否相同，若相同则继续匹配后面的元素，不相同则检查下面一位，所以i不需要回溯，一直向后移动就行，j根据情况需要，前移或后移比较元素是否相同

而next存储的就是相同的元素序列的位置

实现

//串的模式匹配
//KMP算法
#include<iostream>
#include<string>
using namespace std;

void getNext(string T,int next[]){//求next数组
    int i=1,j=0;
    next[1]=0;
    while(i<T.length()){
        if(j==0||T[i-1]==T[j-1]){//下标从0开始
            i++;
            j++;
            next[i]=j;
        }else{
            j=next[j];
        }
    }
}
void Index_KMP(string S,string T,int next[]){
    int i=1,j=1;
    while(i<=S.length()&&j<=T.length()){
        if(j==0||S[i-1]==T[j-1]){
            i++;
            j++;
        }else{
            j=next[j];
        }
    }
    if(j>T.length()){
            cout<<"匹配成功"<<endl;
            cout<<"T在S中的起始位置是:"<<i-T.length()<<endl;
        }else{
            cout<<"匹配失败"<<endl;
        }
}

int main(){
    string str="aaaabcd";
    string ttr="aabc";
    int next[100];
    getNext(ttr,next);
    Index_KMP(str,ttr,next);
}

数组

数组数据结构可以直接利用自带的数组结构实现

特殊矩阵的压缩存储

对称矩阵：

可以用一维数组存储

对称矩阵的实现过程是，若存储下三角中的元素，只需将各元素所在的行标 i 和列标 j 代入下面的公式：

存储上三角的元素要将各元素的行标 i 和列标 j 代入另一个公式：

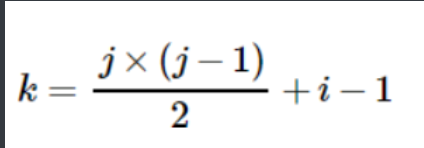
上下三角矩阵：也用一维数组存

稀疏矩阵:

矩阵中分布大量的0

只存非零元素

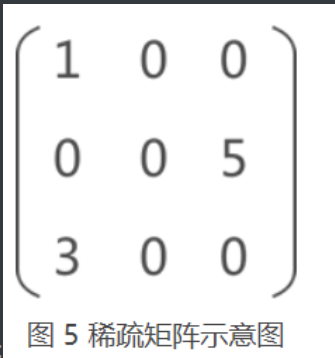
例如，存储图 5 中的稀疏矩阵，需存储以下信息：

• (1,1,1)：数据元素为 1，在矩阵中的位置为 (1,1)；
• (3,3,1)：数据元素为 3，在矩阵中的位置为 (3,1)；
• (5,2,3)：数据元素为 5，在矩阵中的位置为 (2,3)；
• 除此之外，还要存储矩阵的行数 3 和列数 3；

三元顺序表，稀疏矩阵的三元组表示

将稀疏矩阵压缩为三元组数组

//三元组存储稀疏矩阵
#include<iostream>
using namespace std;
#define number 20
class triple{
    public:
    int i,j;//行标i，列标j
    int data;//元素值
};

class TSMatrix{
    public:
    triple data[20];
    int n,m,num;//n:行数;m:列数;num:非零元素个数;
};

void initTsMatrix(TSMatrix &T){
    T.m=3;
    T.n=3;
    T.num=3;//三行三列三个非零元素的稀疏矩阵

    T.data[0].i=1;
    T.data[0].j=1;
    T.data[0].data=1;

    T.data[1].i=2;
    T.data[1].j=3;
    T.data[1].data=5;

    T.data[2].i=3;
    T.data[2].j=1;
    T.data[2].data=3;
}

void display(TSMatrix T){
    for(int i=1;i<=T.n;i++){//非零元素的位置是从1开始的
        for(int j=1;j<=T.m;j++){
            int value=0;
            for(int k=0;k<T.num;k++){
                if(i==T.data[k].i && j==T.data[k].j){
                    cout<<T.data[k].data<<" ";
                    value=1;
                    break;
                }  
            }
            if(value==0){
                cout<<"0"<<" ";
            }


        }
        cout<<endl;
    }
}

int main(){
    TSMatrix T;
    initTsMatrix(T);
    display(T);
}

 

广义表

定义

广义表，又称列表，广义表中既可以存储不可再分的元素，也可以存储广义表

通常，广义表中的单个元素称为“原子”，存储的广义表称为“子表”

类似数学中的集合

表头和表尾

当广义表非空时，称第一个数据为表头，可以是单个元素或子表。剩下的数据构成的新的广义表为表尾

eg：在广义表中 LS={1,{1,2,3},5} 中，表头为原子 1，表尾为子表 {1,2,3} 和原子 5 构成的广义表，即 {{1,2,3},5}。

再比如，在广义表 LS = {1} 中，表头为原子 1 ，但由于广义表中无表尾元素，因此该表的表尾是一个空表，用 {} 表示。

实现

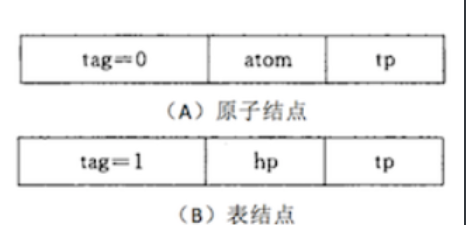
表示原子的节点构成由 tag 标记位、原子值和 tp 指针构成，表示子表的节点还是由 tag 标记位、hp 指针和 tp 指针构成。

 

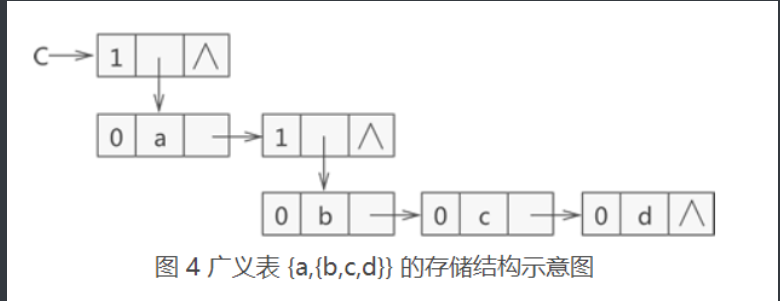
//广义表
//存储表{a,{b,c,d}};
#include <iostream>
using namespace std;

class glist{
public:
    int tag;   //标志域
    char atom; //原子节点值域
    glist *hp; //指向表头
    glist *tp; //指向下一个元素
};

typedef glist *Glist;

void createList(Glist &L){
    //节点1
    L = (Glist)malloc(sizeof(glist));
    L->tag = 1;
    L->hp = (Glist)malloc(sizeof(glist));
    L->tp = NULL;
    //节点2
    L->hp->tag = 0;
    L->hp->atom = 'a';
    L->hp->tp = (Glist)malloc(sizeof(glist));
    //节点3
    L->hp->tp->tag = 1;
    L->hp->tp->hp = (Glist)malloc(sizeof(glist));
    L->hp->tp->tp = NULL;
    //节点4
    L->hp->tp->hp->tag = 0;
    L->hp->tp->hp->atom = 'b';
    L->hp->tp->hp->tp = (Glist)malloc(sizeof(glist));
    //节点5
    L->hp->tp->hp->tp->tag = 0;
    L->hp->tp->hp->tp->atom = 'c';
    L->hp->tp->hp->tp->tp = (Glist)malloc(sizeof(glist));
    //节点6
    L->hp->tp->hp->tp->tp->tag = 0;
    L->hp->tp->hp->tp->tp->atom = 'd';
    L->hp->tp->hp->tp->tp->tp = (Glist)malloc(sizeof(glist));
    //结束标志
    L->hp->tp->hp->tp->tp->tp->tag=-1;
}
// tap==1,则L的下级有值，L=L->hp
// tap==0,L的同级有值，L=L->tp
//退出的条件是tag==0&&L->tp==NULL(非空表)
void display(Glist L){
    while(1){
        if (L->tag==1){
            L = L->hp;
            cout<<"{";
        }else if(L->tag==0){
            cout << L->atom;
            L = L->tp;
        }else{
            break;
        }
    }
    cout<<"}";

}

int main(){
    Glist L;
    createList(L);
    display(L);

}