P1744 采购特价商品

题目描述

中山路店山店海，成了购物狂爱与愁大神的“不归之路”。中山路上有$n(n\leqslant 100)$家店，每家店的坐标均在$-10000\sim 10000$之间。其中的$m$家店之间有通路。若有通路，则表示可以从一家店走到另一家店，通路的距离为两点间的直线距离。现在爱与愁大神要找出从一家店到另一家店之间的最短距离。你能帮爱与愁大神算出吗？

输入格式

共$n+m+3$行：

第$1$行：整数$n$

第$2$行到第$n+1$行：每行两个整数$x$和$y$，描述了一家店的坐标

第$n+2$行：整数$m$

第$n+3$行到第$n+m+2$行：每行描述一条通路，由两个整数$i$和$j$组成，表示第$i$家店和第$j$家店之间有通路。

第$n+m+3$行：两个整数$s$和$t$，分别表示原点和目标店

输出格式

仅一行：一个实数（保留两位小数），表示从$s$到$t$的最短路径长度。

样例数据

输入

5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5

输出

3.41

分析

两点间距离公式：

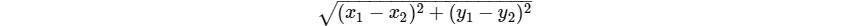
 然后就是$SPFA$模板，更改起始点终止点即可

代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')
#define MAXN 2000100
#define INF 1000000000.0

using namespace std;

typedef long long ll;
typedef double Db;

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

struct Edge
{
    int To , Next;
    Db Dis;
}E[MAXN];

int Head[MAXN] , Count , n;
bool Visit[MAXN];
Db Dis[MAXN];
int x[MAXN] , y[MAXN];
int Start , End;

inline Db Distance(int a1 , int b1 , int a2 , int b2)
{
    int Delta_X = a1 - a2;
    int Delta_Y = b1 - b2;
    return sqrt(abs(Delta_X) * abs(Delta_X) + abs(Delta_Y) * abs(Delta_Y));
}

inline void Add_Edge(int u , int v , Db d)
{
    E[++Count].Dis = d;
    E[Count].To = v;
    E[Count].Next = Head[u];
    Head[u] = Count;
}

queue <int> Q;

inline void SPFA()
{
    for(int i = 1; i <= n; i++)
    {
        Dis[i] = INF;
        Visit[i] = false;    
    }
    Dis[Start] = 0;
    Q.push(Start);
    Visit[Start] = true;
    while(!Q.empty())
    {
        int u = Q.front();
        Q.pop();
        Visit[u] = false;
        for(int i = Head[u]; i; i = E[i].Next)
        {
            int v = E[i].To;
            if(Dis[v] > E[i].Dis + Dis[u])
            {
                Dis[v] = E[i].Dis + Dis[u];
                if(!Visit[v])
                    Q.push(v);
            }
        }
    }
}

int main()
{
    n = Read();
    for(int i = 1; i <= n; i++)
        x[i] = Read() , y[i] = Read();
    int m = Read();
    while(m--)
    {
        int u = Read() , v = Read();
        Db d = Distance(x[u] , y[u] , x[v] , y[v]);
        Add_Edge(u , v , d);
        Add_Edge(v , u , d);
    }
    Start = Read() , End = Read();
    SPFA();
    printf("%.2lf" , Dis[End]);
    return 0;
}