混合背包问题

题目描述

一个旅行者有一个最多能用$V$公斤的背包，现在有$n$件物品，它们的重量分别是$W_1，W_2，...,W_n$，它们的价值分别为$C_1,C_2,...,C_n$。有的物品只可以取一次（01背包），有的物品可以取无限次（完全背包），有的物品可以取的次数有一个上限（多重背包）。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

输入格式

输入有多组数据，对于输入每组数据的第一行：二个整数，$V$(背包容量，$V\leqslant 200$)，$N$(物品数量，$N\leqslant 200$)；
第$2..N+1$行：每行三个整数$W_i,C_i,P_i$，前两个整数分别表示每个物品的重量，价值，第三个整数若为$0$，则说明此物品可以购买无数件，若为其他数字，则为此物品可购买的最多件数($P_i$)。

输出格式

对于每组输入输出仅一行，一个数，表示最大总价值。

样例数据

输入

10 3
2 1 0
3 3 1
4 5 4

输出

11

分析

首先判断$P_i$是否等于$0$，如果等于，那么就是完全背包的板子，否则就是多重背包的板子，最后$Dp_V$即为答案，代表容量为$V$的背包所能装的最大价值

状态转移方程：

完全背包或01背包

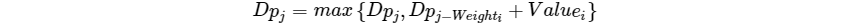
 多重背包

代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')
#define MAXN 2000100
#define INF 1e6

using namespace std;

typedef long long ll;
typedef double Db;

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

int Weight[10001] , Value[10001] , P[10001];
int Dp[10001];

int main()
{
    int V = Read() , N = Read();
    for(int i = 1; i <= N; i++)
        Weight[i] = Read() , Value[i] = Read() , P[i] = Read();
    for(int i = 1; i <= N; i++)
    {
        if(P[i] == 0)
            for(int j = Weight[i]; j <= V; j++)
                Dp[j] = max(Dp[j] , Dp[j - Weight[i]] + Value[i]);
        else
            for(int j = V; j >= 0; j--)
                for(int k = 1; k <= P[i]; k++)
                    if(j - k * Weight[i] >= 0)
                    Dp[j] = max(Dp[j] , Dp[j - k * Weight[i]] + k * Value[i]);
    }
    Write(Dp[V]);
    return 0;
}

/*
10 3
2 1 0
3 3 1
4 5 4

11
*/