关于差分约束的一点理解

引例

给定$n$个变量和$m$个不等式，每个不等式形如$x_i-x_j\leqslant a_k$，求$x_{n-1}-x_0$的最大值$0<i,j\leqslant n$

$x_1-x_0\leqslant 2 \\x_2-x_0\leqslant 7 \\x_3-x_0\leqslant 8 \\x_2-x_1\leqslant 3 \\x_3-x_2\leqslant 2 $

变形得到

$x_3-x_0\leqslant 8 \\x_3-x_0\leqslant 9 \\x_3-x_0\leqslant 7$

对于每个不等式$x_i-x_j\leqslant a_k$，对结点$j$和$i$建立一条$j\rightarrow i$的有向边，边权为$a_k$，求$x_{n-1}-x_0$的最大值即为求$0$到$n-1$的最短路

类似于SPFA的松弛操作

SPFA的松弛操作：如果$d_u+w(u,v)<d_v$，那么更新$d_v=d_u+w(u,v)$

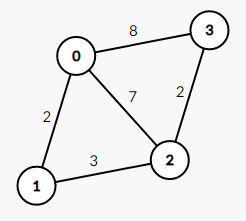
差分约束

数形结合

变形原不等式得到

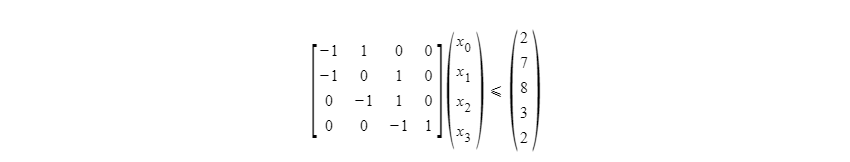
$x_i-x_j\leqslant a_k$得到$x_i\leqslant x_j+a_k$。

令$i=v,j=u,d=x$，可以得到$d_v\leqslant d_u+w(j,i)$

SPFA的松弛操作$if(d_u+w(u,v)<d_v)$那么$d_v=d_u+w(u,v)$，即为$d_u+w(u,v)\geqslant d_v$ 

三角不等式

$B-A\leqslant c①\\C-B\leqslant a②\\C-A\leqslant b③$

 

 

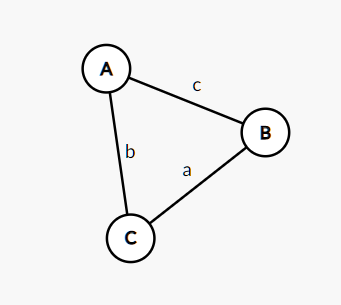
 要求$C-A$的最大值，只需$①+②$，即可得到$C-A\leqslant a+c$，本质上就是求$min(b,a+c)$，三角不等式推广到$m$个，变量推广为$n$个，就变成$n$个点$m$条边的最短路问题

判断是否有解

最短路会出现负权圈或者根本就不可达的情况，所以在不等式组转化的图上也有可能出现三种情况

·有解

·无解

·有无限多解

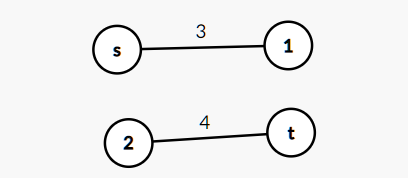
$x_t-x_s$最大值不存在

有负环

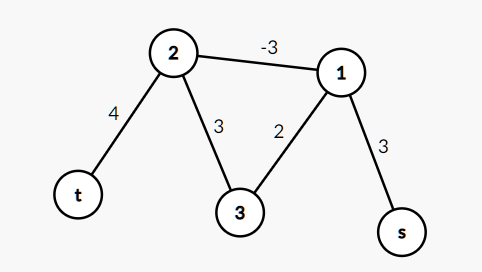
$x_t-x_s$最大值无限大

不相连

最小值问题

改变符号即可

不等式的标准化

既有$ \leqslant$又有$ \geqslant$

如果需要求的是两个变量差的最大值，那么需要将所有不等式转变成$ \leqslant $的形式，建图后求最短路
相反，如果需要求的是两个变量差的最小值，那么需要将所有不等式转化成$ \geqslant $，建图后求最长路

形如$A-B=c$

转化为$A-B\leqslant c①\\A-B\geqslant c②$，建图

整数域，形如$A-B<c$

变形，整理成$A-B\leqslant c-k(k \in Z)$