微分中值定理与简单例题

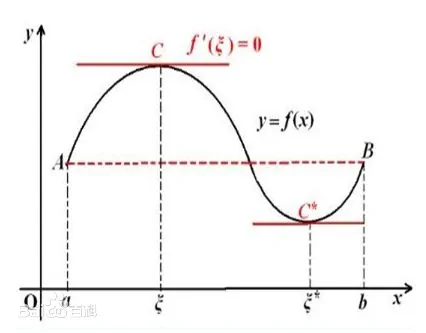
罗尔中值定理

描述

如果$R$上的函数$f(x)$满足以下条件：

（1）在闭区间$[a,b]$上连续

（2）在开区间$(a,b)$内可导

（3）$f(a) = f(b)$

则至少存在一个$ξ∈(a,b)$，使得$f'(ξ)=0$。

证明

因为函数$f(x)$在闭区间$[a,b] $上连续，所以存在最大值与最小值，分别用 $M $和 $m$ 表示，分两种情况讨论：

1. 若 $M=m$，则函数 $f(x)$ 在闭区间 $[a,b]$ 上必为常函数，结论显然成立。

2. 若 $M>m$，则因为 $f(a)=f(b)$ 使得最大值 $M$ 与最小值 $m$ 至少有一个在 $(a,b)$ 内某点$ξ$处取得，从而$ξ$是$f(x)$的极值点，又条件 $f(x)$ 在开区间 $(a,b)$ 内可导得，$f(x)$ 在 $ξ$ 处取得极值，由费马引理，可导的极值点一定是驻点，推知：$f'(ξ)=0$。

拉格朗日中值定理

描述

如果$R$上的函数$f(x)$满足以下条件：

（1）在闭区间$[a,b]$上连续

（2）在开区间$(a,b)$内可导

则至少存在一个$ξ∈(a,b)$，使得$f'(ξ)=\frac{f(a)-f(b)}{a-b}$

拉格朗日中值公式

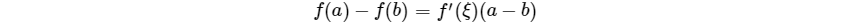
证明

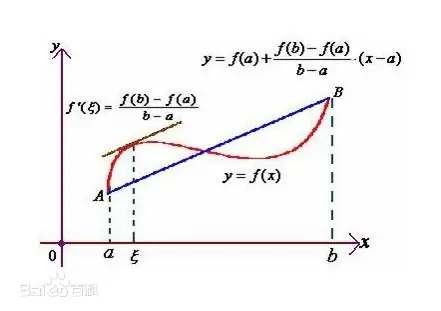
令$g(x) = f(x)-f(a)-\frac{f(a)-f(b)}{a-b}(x-a)$，可得$g(a)=g(b)$，又根据罗尔中值定理，必有$g'(\xi)=f'(\xi)-\frac{f(a)-f(b)}{a-b}=0$，变形得$f(a)-f(b)=f'(\xi)(a-b)$

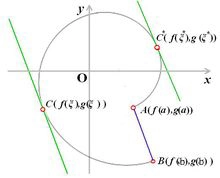
柯西中值定理

描述

如果$R$上的函数$f(x),g(x)$满足以下条件：

（1）在闭区间$[a,b]$上连续

（2）在开区间$(a,b)$内可导

则至少存在一个$ξ∈(a,b)$，使得$\frac{f(a)-f(b)}{g(a)-g(b)}=\frac{f'(\xi)}{g'(\xi)}$

证明

令$F(x)=[f(a)-f(b)][g(x)-g(a)]-[g(a)-g(b)][f(x)-f(a)]$，$F(a)=F(b)=0$，又根据罗尔中值定理，必有$[f(a)-f(b)]g'(\xi)-[g(a)-g(b)]f'(\xi)=0$，所以有$\frac{f(a)-f(b)}{g(a)-g(b)}=\frac{f'(\xi)}{g'(\xi)}$

例题

e.g.1

求证：$x>1$时，$e^{x}>ex$

证明：令$f(x)=e^{x}$，显然$f(x)$满足拉格朗日中值定理使用条件。则在区间$(1,x)$内，由拉格朗日中值定理可知，$f(x)-f(1)=f'(\xi)(x-1)$，得$e^{x}-e=e^{\xi}(x-1)$，又因为$\xi\in (1,x),x>1$，故$e^{\xi}(x-1)>0$，所以$e^{x}-e>0$，即$e^{x}>e$，$Q.E.D$

e.g.2

求证：当$0<a<b$时，$\frac{a-b}{b}<ln\frac{a}{b}<\frac{a-b}{a}$

证明：$ln\frac{a}{b}=lna-lnb$，令$f(x)=lnx$，显然$f(x)$满足拉格朗日中值定理使用条件。$f(a)-f(b)=f'(\xi)(a-b)$，所以$f(a)-f(b)=\frac{a-b}{\xi}$，因为$\xi\in (a,b),a<b$，所以$\frac{a-b}{b}<lna-lnb<\frac{a-b}{a}$即$\frac{a-b}{b}<ln\frac{a}{b}<\frac{a-b}{a}$，$Q.E.D$

e.g.3

求证：$a>b>0,n>1$时，$nb^{n-1}(a-b)<a^n-b^n<na^{n-1}(a-b)$

证明：令$f(x)=x^n$，显然$f(x)$满足拉格朗日中值定理使用条件。$f(a)-f(b)=f'(\xi)(a-b)$，所以$a^n-b^n=n\xi^{n-1}(a-b)$，又因为$\xi\in(b,a)$，所以$nb^{n-1}(a-b)<a^n-b^n<na^{n-1}(a-b)$，$Q.E.D$