P4779 【模板】单源最短路径(标准版)单源最短路Dijkstra
题目描述
给定一个$n$个点,$m$条有向边的带非负权图,请你计算从$s$出发,到每个点的距离。
数据保证你能从$s$出发到任意点。
输入格式
第一行为三个正整数$n,m,s$。 第二行起$m$行,每行三个非负整数 $u_i, v_i, w_i$,表示从$u_i$到$v_i$有一条权值为$w_i$的有向边。
输出格式
输出一行$n$个空格分隔的非负整数,表示$s$到每个点的距离。
输入输出样例
输入
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
输出
0 2 4 3
样例解释
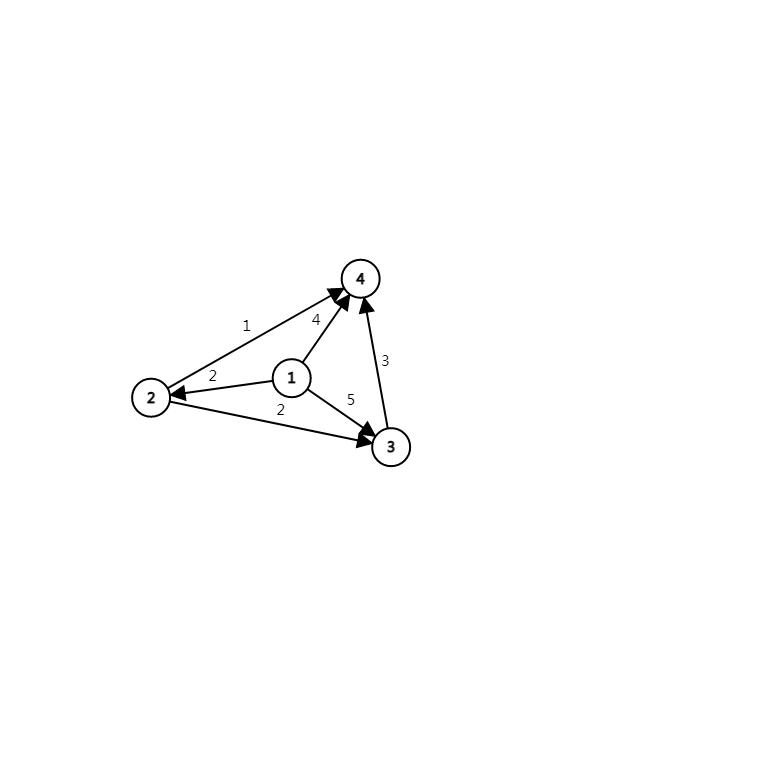
由$1\rightarrow 1$,距离为$0$,由$1\rightarrow 2$,距离为$2$,由$1\rightarrow 3$,距离最小等于$1\rightarrow 2\rightarrow 3 = 4$,由$1\rightarrow 4$,距离最小等于$1\rightarrow 2\rightarrow 4 = 3$
分析
模板题,裸$Dijkstra$即可
代码
#include <bits/stdc++.h> #define Enter puts("") #define Space putchar(' ') using namespace std; typedef long long ll; typedef double Db; inline ll Read() { ll Ans = 0; char Ch = getchar() , Las = ' '; while(!isdigit(Ch)) { Las = Ch; Ch = getchar(); } while(isdigit(Ch)) { Ans = (Ans << 3) + (Ans << 1) + Ch - '0'; Ch = getchar(); } if(Las == '-') Ans = -Ans; return Ans; } inline void Write(ll x) { if(x < 0) { x = -x; putchar('-'); } if(x >= 10) Write(x / 10); putchar(x % 10 + '0'); } const int MAXN = 100010 , MAXM = 500010; struct Edge { int To , Dis , Next; }; Edge E[MAXM]; int Head[MAXN] , Dis[MAXN] , Count; bool Visit[MAXN]; int n , m , s; inline void Add_Edge(int u , int v , int d) { E[++Count].Dis = d; E[Count].To = v; E[Count].Next = Head[u]; Head[u] = Count; } struct Node { int Dis; int Position; bool operator < (const Node &x)const { return x.Dis < Dis; } }; priority_queue <Node> Q; inline void Dijkstra() { Dis[s] = 0; Q.push((Node) {0 , s}); while(!Q.empty()) { Node Temp = Q.top(); Q.pop(); int x = Temp.Position , d = Temp.Dis; if(Visit[x]) continue; Visit[x] = 1; for(int i = Head[x]; i; i = E[i].Next) { int y = E[i].To; if(Dis[y] > Dis[x] + E[i].Dis) { Dis[y] = Dis[x] + E[i].Dis; if(!Visit[y]) Q.push((Node) {Dis[y] , y}); } } } } int main() { n = Read(); m = Read(); s = Read(); for(int i = 1; i <= n; i++) Dis[i] = 0x7fffffff; for(int i = 0; i < m; i++) { int u , v , d; u = Read(); v = Read(); d = Read(); Add_Edge(u , v , d); } Dijkstra(); for(int i = 1; i <= n; i++) Write(Dis[i]) , Space; return 0; }

