1996:登山
题目描述
五一到了,PKU-ACM队组织大家去登山观光,队员们发现山上一个有$N$个景点,并且决定按照顺序来浏览这些景点,即每次所浏览景点的编号都要大于前一个浏览景点的编号。同时队员们还有另一个登山习惯,就是不连续浏览海拔相同的两个景点,并且一旦开始下山,就不再向上走了。队员们希望在满足上面条件的同时,尽可能多的浏览景点,你能帮他们找出最多可能浏览的景点数么?
输入格式
第一行:$N(2\leqslant N\leqslant 1000)$景点数
第二行: $N$个整数,每个景点的海拔
输出格式
一行整数,表示最多能浏览的景点数
分析
与合唱队形基本相同,均为最长不下降子序列接最长不上升子序列,但是要求输出结果不同,合唱队形是$N-Ans$,本题只需输出$Ans$即可
状态转移方程
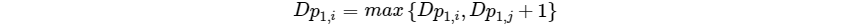
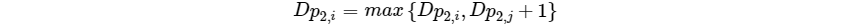
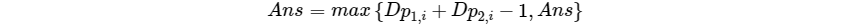
代码
#include <bits/stdc++.h> #define Enter puts("") #define Space putchar(' ') using namespace std; typedef long long ll; typedef double Db; inline ll Read() { ll Ans = 0; char Ch = getchar() , Las = ' '; while(!isdigit(Ch)) { Las = Ch; Ch = getchar(); } while(isdigit(Ch)) { Ans = (Ans << 3) + (Ans << 1) + Ch - '0'; Ch = getchar(); } if(Las == '-') Ans = -Ans; return Ans; } inline void Write(ll x) { if(x < 0) { x = -x; putchar('-'); } if(x >= 10) Write(x / 10); putchar(x % 10 + '0'); } int T[100001]; int Dp[10][10001]; int Ans; int main() { int n; n = Read(); for(int i = 1; i <= n; i++) T[i] = Read(); T[0] = 0; for(int i = 1; i <= n; i++) for(int j = 0; j < i; j++) if(T[i] > T[j]) Dp[1][i] = max(Dp[1][i] , Dp[1][j] + 1); T[n + 1] = 0; for(int i = n; i > 0; i--) for(int j = n + 1; j > i; j--) if(T[i] > T[j]) Dp[2][i] = max(Dp[2][i] , Dp[2][j] + 1); for(int i = 1; i <= n; i++) Ans = max(Dp[1][i] + Dp[2][i] - 1, Ans); Write(Ans); return 0; }

