最长公共子序列（LCS）

题目描述

我们称序列$Z=\left \langle z_{1},z_{2},...,z_{k}\right \rangle$是序列$X=\left \langle x_{1},x_{2},...,x_{m}\right \rangle$的子序列当且仅当存在 严格上升 的序列$\left \langle i_{1},i_{2},...,i_{k}\right \rangle$，使得对$j=1,2,...,k$，有$x_{i_{j}}=z_{j}$。比如$Z=\left \langle a,b,f,c\right \rangle$是$X=\left \langle a,b,c,f,b,c\right \rangle$的子序列

现在给出两个序列$X$和$Y$，你的任务是找到$X$和$Y$的最大公共子序列，也就是说要找到一个最长的序列$Z$，使得$Z$既是$X$的子序列也是$Y$的子序列。

输入格式

输入包括多组测试数据。每组数据包括一行，给出两个长度不超过$200$的字符串，表示两个序列。两个字符串之间由若干个空格隔开。

输出格式

对每组输入数据，输出一行，给出两个序列的最大公共子序列的长度。

样例数据

输入

abcfbc         abfcab
programming    contest 
abcd           mnp

输出

4
2
0

分析

如果$A_{i}=B_{j}$的话，那么$Dp_{i,j}=Dp_{i-1,j-1}+1$，其中$Dp_{i,j}$表示序列$A$在第$i$个元素之前与序列$B$在第$j$个元素之前最长公共子序列的长度

状态转移方程

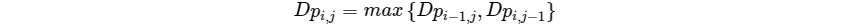
代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')

using namespace std;

typedef long long ll;
typedef double Db;

inline ll Read() 
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch)) 
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch)) 
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x) 
{
    if(x < 0) 
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

char a[1001] , b[1001];
int Dp[1001][1001];
int main() 
{
    while(~scanf("%s%s" , a + 1 , b + 1)) 
    {
        int n = strlen(a + 1);
        int m = strlen(b + 1);
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                if(a[i] == b[j])
                    Dp[i][j] = Dp[i - 1][j - 1] + 1;
                else
                    Dp[i][j] = max(Dp[i - 1][j] , Dp[i][j - 1]);
        Write(Dp[n][m]) , Enter;
        memset(Dp , 0 , sizeof(Dp));
    }
    return 0;
}