记忆化搜索与路径输出

引例

在一个地图上有$N$个地窖$\left ( N\leqslant 200\right )$，每个地窖中埋有一定数量的地雷。同时，给出地窖之间的连接路径，并规定路径都是单向的，也不存在可以从一个地窖出发经过若干地窖后又回到原来地窖的路径。某人可以从任意一处开始挖地雷，然后沿着指出的连接往下挖，（仅能选择一条路径），当无连接时挖地雷工作结束。设计一个挖地雷方案，使他能挖到最多的地雷

样例数据

输入

6
5 10 20 5 4 5 
1 2
1 4
2 4
3 4
4 5
4 6
5 6
0 0

输出

3-4-5-6
34

分析

记忆化搜索，注意建边加边及输出格式。

状态转移方程

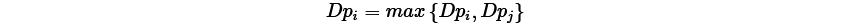
 其中$Dp_{j}$表示从$j$出发，能挖到的最多地雷数，然后枚举每一个点

代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')

using namespace std;

typedef long long ll;
typedef double Db;

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

struct Edge
{
    int To , Nxt;
}E[100001];

int Head[10001] , Next[10001];
int Edge_Count;
int n , a[10001] , Ans , Dp[10001]; 

inline void Add_Edge(int x , int y)
{
    E[++Edge_Count].Nxt = Head[x];
    E[Edge_Count].To = y;
    Head[x] = Edge_Count;
}

inline int DFS(int x)
{
    if(Dp[x])
        return Dp[x];
    Dp[x] = a[x];
    for(int i = Head[x]; i; i = E[i].Nxt)
    {
        int T = DFS(E[i].To);
        if(Dp[x] < T + a[x])
        {
            Dp[x] = T + a[x];
            Next[x] = E[i].To;
        }
    }
    return Dp[x];
}

int main()
{
    n = Read();
    for(int i = 1; i <= n; i++)
        a[i] = Read();
    int u , v;
    while(1)
    {
        u = Read();
        v = Read();
        if(u == 0 && v == 0)
            break;
        Add_Edge(u , v);
    }
    int Start;
    for(int i = 1; i <= n; i++)
        if(Ans < DFS(i))
        {
            Ans = DFS(i);
            Start = i;
        }
    while(Start)
    {
        Write(Start);
        Start = Next[Start];
        if(Start)
            putchar('-');
    }
    Enter;
    Write(Ans);
    return 0;
}