Floyd最短路及路径输出

引例

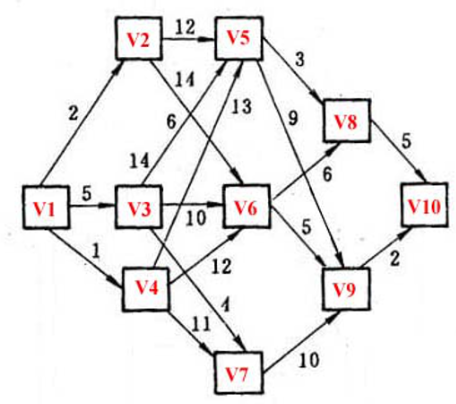
下图表示城市之间的交通路网，线段上的数字表示费用。如图，求$V_{1}$→$V_{n}$最短路径长度及路径

样例数据

输入

10
0 2 5 1 0 0 0 0 0 0
0 0 0 0 12 14 0 0 0 0
0 0 0 0 6 10 4 0 0 0
0 0 0 0 13 12 11 0 0 0
0 0 0 0 0 0 0 3 9 0
0 0 0 0 0 0 0 6 5 0
0 0 0 0 0 0 0 0 10 0
0 0 0 0 0 0 0 0 0 5
0 0 0 0 0 0 0 0 0 2
0 0 0 0 0 0 0 0 0 0

输出

minlong=19
1 3 5 8 10

分析

用$Dp$数组记录状态并初始化之为$INF$，如果输入的$G_{i, j}$不是0则$Dp_{i, j}$ = $G_{i, j}$。裸$Floyd$，$Path$数组记录路径，递归输出，输出时勿忘判断此时是否存在$Path$，且要先输出1因为从1开始且1不会被判断到

代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')

using namespace std;

typedef long long ll;
typedef double Db;

const int INF = 0x3f3f3f;

//template <typename T>

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

int G[1001][1001];
int n;
int Dp[1001][1001];
int Path[1001][1001];

inline void Print_Path(int x , int y)
{
    if(x == y) 
    {
        printf("%d" , x);
        return ;
    }
    int k = Path[x][y];
    if(Path[x][y])
        Print_Path(x , k);        
    printf("%d " , y);
}

/*inline void Init()
{ 
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= n; j ++ )
        {
            if(i == j) 
                Dp[i][j] = 0;
            else 
                Dp[i][j] = INF;
            Path[i][j] = i;
        }            
}*/

int main()
{
    n = Read();
    //Init();
    memset(Dp , INF , sizeof(Dp));
    for(int i = 1; i <= n; i++)    
        for(int j = 1; j <= n; j++)
        {
            G[i][j] = Read();
            if(G[i][j])
                Dp[i][j] = G[i][j];    
        }
/*    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            if(!Dp[i][j]) 
                Dp[i][j] = INF;
*/
    for(int i = 1; i <= n; i++)
        Dp[i][i] = 0;
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
            {
                if(Dp[i][j] > Dp[i][k] + Dp[k][j])
                {
                    Dp[i][j] = Dp[i][k] + Dp[k][j];
                    Path[i][j] = k;
                }
            }
    printf("minlong=%d" , Dp[1][n]);
    Enter;
    cout << "1 ";
    Print_Path(1 , n);
    return 0;
}