P1045 [NOIP2003 普及组] 麦森数
题目描述
形如2^P−1的素数称为麦森数,这时P一定也是个素数。但反过来不一定,即如果P是个素数,2^P−1不一定也是素数。
到1998年底,人们已找到了37个麦森数。最大的一个是P=3021377,它有909526位。麦森数有许多重要应用,它与完全数密切相关。
任务:从文件中输入P(1000<P<3100000),计算2^P−1的位数和最后500位数字(用十进制高精度数表示)
输入格式
文件中只包含一个整数P(1000<P<3100000)
输出格式
第一行:十进制高精度数2^P−1的位数。
第2-11行:十进制高精度数2^P−1的最后500位数字。(每行输出50位,共输出10行,不足500位时高位补0)
不必验证2^P−1与PP是否为素数。
输入输出样例
输入 #1
1279
输出 #1
386 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000 00000000000000104079321946643990819252403273640855 38615262247266704805319112350403608059673360298012 23944173232418484242161395428100779138356624832346 49081399066056773207629241295093892203457731833496 61583550472959420547689811211693677147548478866962 50138443826029173234888531116082853841658502825560 46662248318909188018470682222031405210266984354887 32958028878050869736186900714720710555703168729087
分析
对于2^p,有
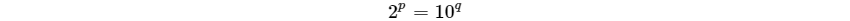
所以
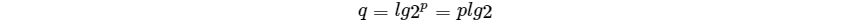
对于10^n,其位数为n+1位,故2^p的位数为
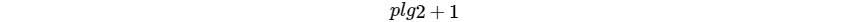
直接输出
其次就是压位高精度
代码
#include <bits/stdc++.h> #define Enter puts("") #define Space putchar(' ') using namespace std; typedef long long ll; typedef double Db; typedef unsigned long long Ull; inline ll Read() { ll Ans = 0; char Ch = getchar() , Las = ' '; while(!isdigit(Ch)) { Las = Ch; Ch = getchar(); } while(isdigit(Ch)) { Ans = (Ans << 3) + (Ans << 1) + Ch - '0'; Ch = getchar(); } if(Las == '-') Ans = -Ans; return Ans; } inline void Write(ll x) { if(x < 0) { x = -x; putchar('-'); } if(x >= 10) Write(x / 10); putchar(x % 10 + '0'); } int a[100001]; const int Maxn = 100000; int main() { int p; p = Read(); Write((int)(p*log10(2.0)+1)); Enter; int left = p % 10; p /= 10; a[0] = 1; for(int i = 1; i <=p; i++) { for(int j = 0; j <= 100; j++) a[j] <<= 10; for(int j = 0; j <= 100; j++) { if(a[j] >= Maxn) { a[j + 1] += a[j] / Maxn; a[j] %= Maxn; } } } for(int i = 1; i <= left; i++) { for(int j = 0; j <= 100; j++) a[j] <<= 1; for(int j = 0; j <= 100; j++) { if(a[j] >= Maxn) { a[j + 1] += a[j] / Maxn; a[j] %= Maxn; } } } a[0]--; for(int i = 99; i >= 0; i--) { printf("%05d" , a[i]); if(i % 10 == 0) Enter; } return 0; }

