关于牛顿迭代与求方程*似解的思考

背景

　　多数方程不存在求根公式，因此求精确根非常困难，甚至不可解，从而寻找方程的*似根就显得特别重要。方法使用函数和f(x)的泰勒级数的前面几项来寻找方f(x)的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附*具有*方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。不说人话

简例

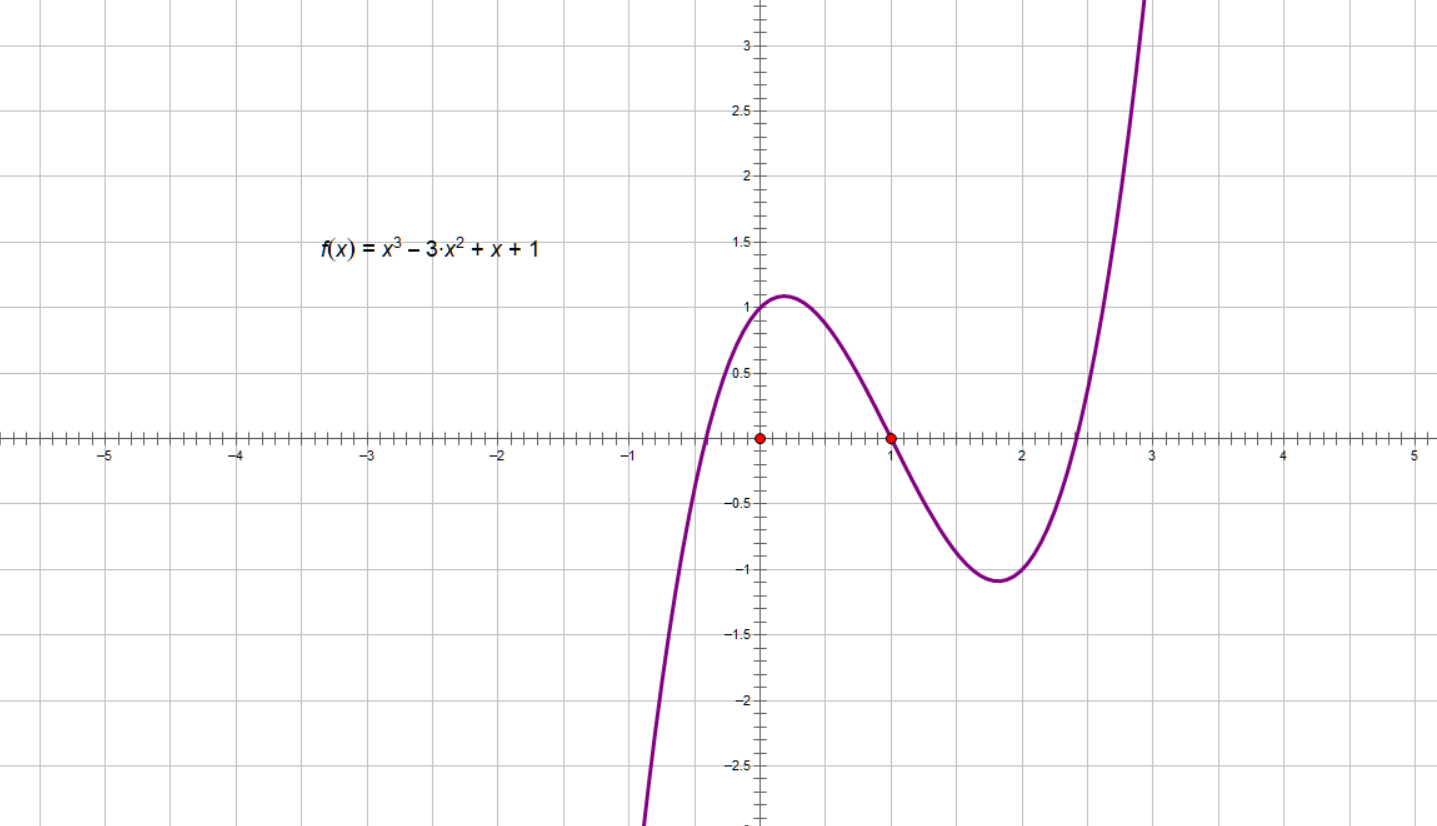
 已知函数f(x) = x^3 - 3x^2 + x + 1,求其三个*似根

我们可取函数上任意点A(x0,f(x0))，过A点做该曲线的切线交x轴与B(x1,0)

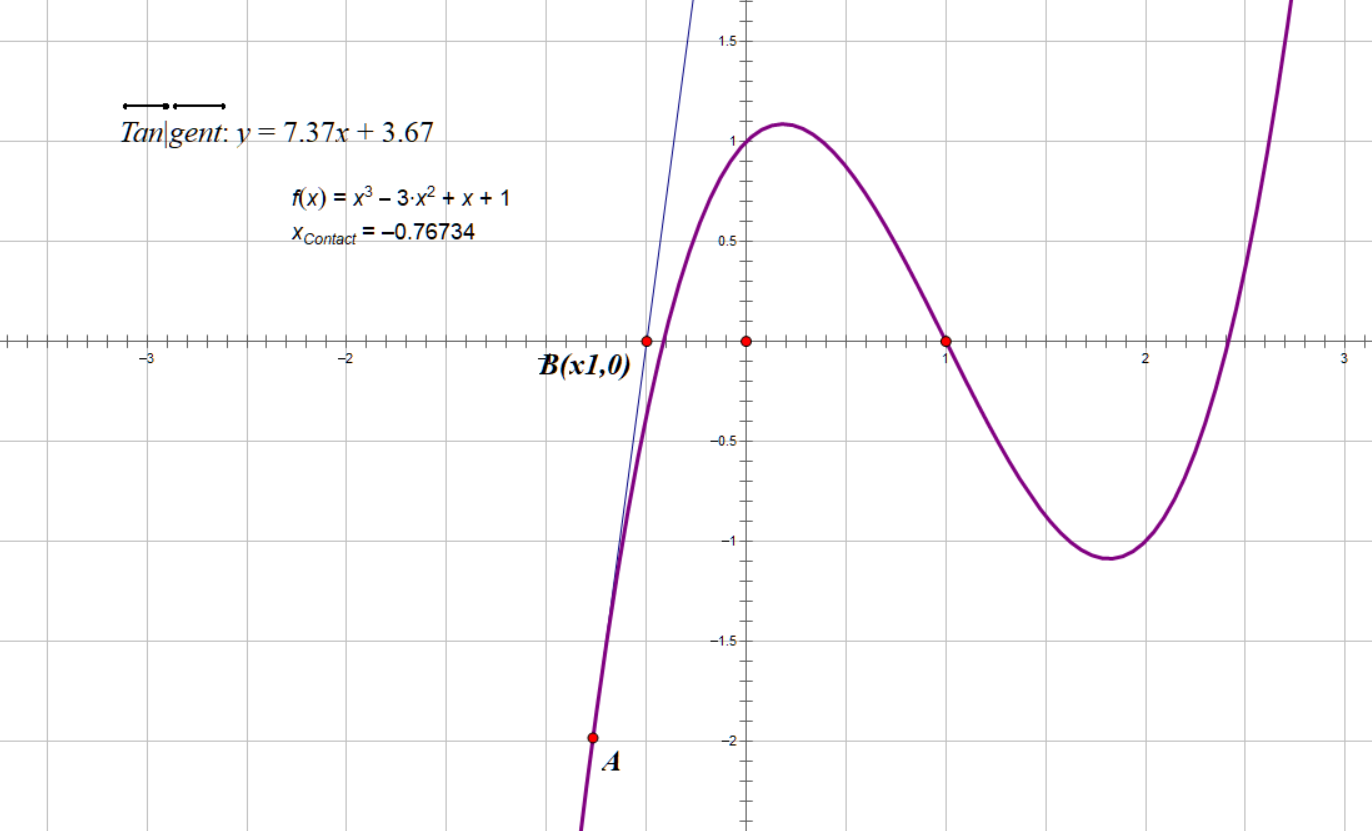
 此时我们可称x1为该函数零点r的一次*似值

过曲线上一点C(x1,f(x1))作切线交x轴与D(x2,0),则称x2为零点r的二次*似值

 

 

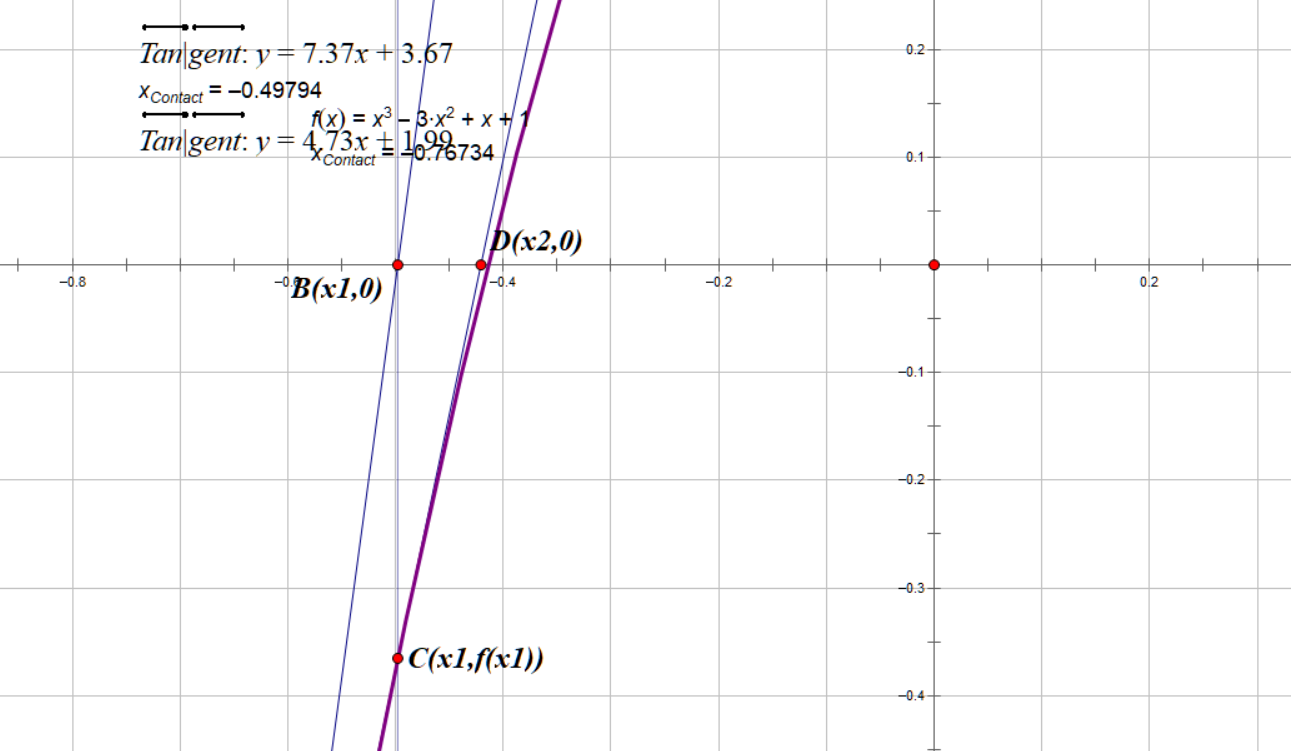
重复以上过程，得r的*似值序列，其中，称为r的n+1次*似值，上式称为牛顿迭代公式。

显而易见，当n→+∞时，此时的n次*似值即为r

已经证明，如果是连续的，并且待求的零点是孤立的，那么在零点周围存在一个区域，只要初始值位于这个邻*区域内，那么牛顿法必定收敛。 并且，如果不为0, 那么牛顿法将具有*方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。

公式推导

取曲线上一点(x0,f(x0)),设该切线过(x1,0)则过该点的切线方程为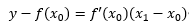

 

进而

 

 移项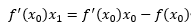

 

 解得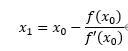

 以此类推

 

 

 

 

 

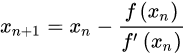
ps：据说要比二分快