P1337 [JSOI2004]平衡点 / 吊打XXX

题目描述

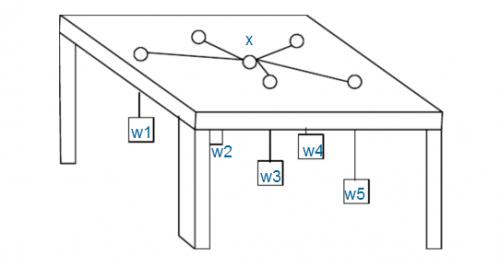
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入格式

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )

输出格式

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

输入输出样例

输入

3
0 2
2 4
1 3

输出

2

分析

应该算紫题里比较简单的一道了，虽然是一道模拟退火的板子题但是我不会，但是直接正交分解移动一点就更新一点长度还是很简单的

程序

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')

using namespace std;

typedef long long ll;
typedef unsigned long long Ull;
typedef double Db;

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

int n , X[100001] , Y[100001] , Weight[100001];
Db x , y  , Length = 10000.0;

inline Db E(Db x)
{
    return x * x;
}

inline void Move(Db l)
{
    Db New_X = 0 , New_Y = 0 , G;
    for(int i = 1; i <= n; i++)
    {
        G = sqrt(E(X[i] - x) + E(Y[i] - y));
        if(G == 0)
            continue;
        New_X += Weight[i] / G * (X[i] - x);
        New_Y += Weight[i] / G * (Y[i] - y);
    }
    G = sqrt(New_X * New_X + New_Y * New_Y);
    x += l / G * New_X;
    y += l / G * New_Y;
}
int main()
{
    n = Read();
    for(int i = 1; i <= n; i++)
    {
        X[i] = Read();
        Y[i] = Read();
        Weight[i] = Read();
    }
    while(Length > 4e-4)
    {
        Move(Length);
        Length *= 0.9;    
    }
    printf("%.3f %.3f" , x , y);
    return 0;
}