GAMES102 Lecture 01
Lecture 01
-
图像是离散的像素
-
图形是具有数学意义的点、线、面,是连续的,有数学表达的
-
渲染是在解积分方程
-
仿真是在解偏微分方程
函数拟合
线性空间
- 元素之间有运算:加法、数乘
- 线性结构:对加分和数乘封闭
- 加法交换律、结合了、数乘分配律
- 基/维数:\(L=span\{V_1,V_2,...,V_N\} = \{\sum_{i=1}^na_iV_i\vert a_i\in R\}\)
- 每个元素就表达(对应)为\(n\)个实数,即一个向量\((a_1,a_2,...,a_n)\)
- 例子
- 欧氏空间:1D空间、2D平面、3D空间
- \(n\)次多项式:\(f(x)sum_{k=0}^na_kx^k\)
映射 (mapping)
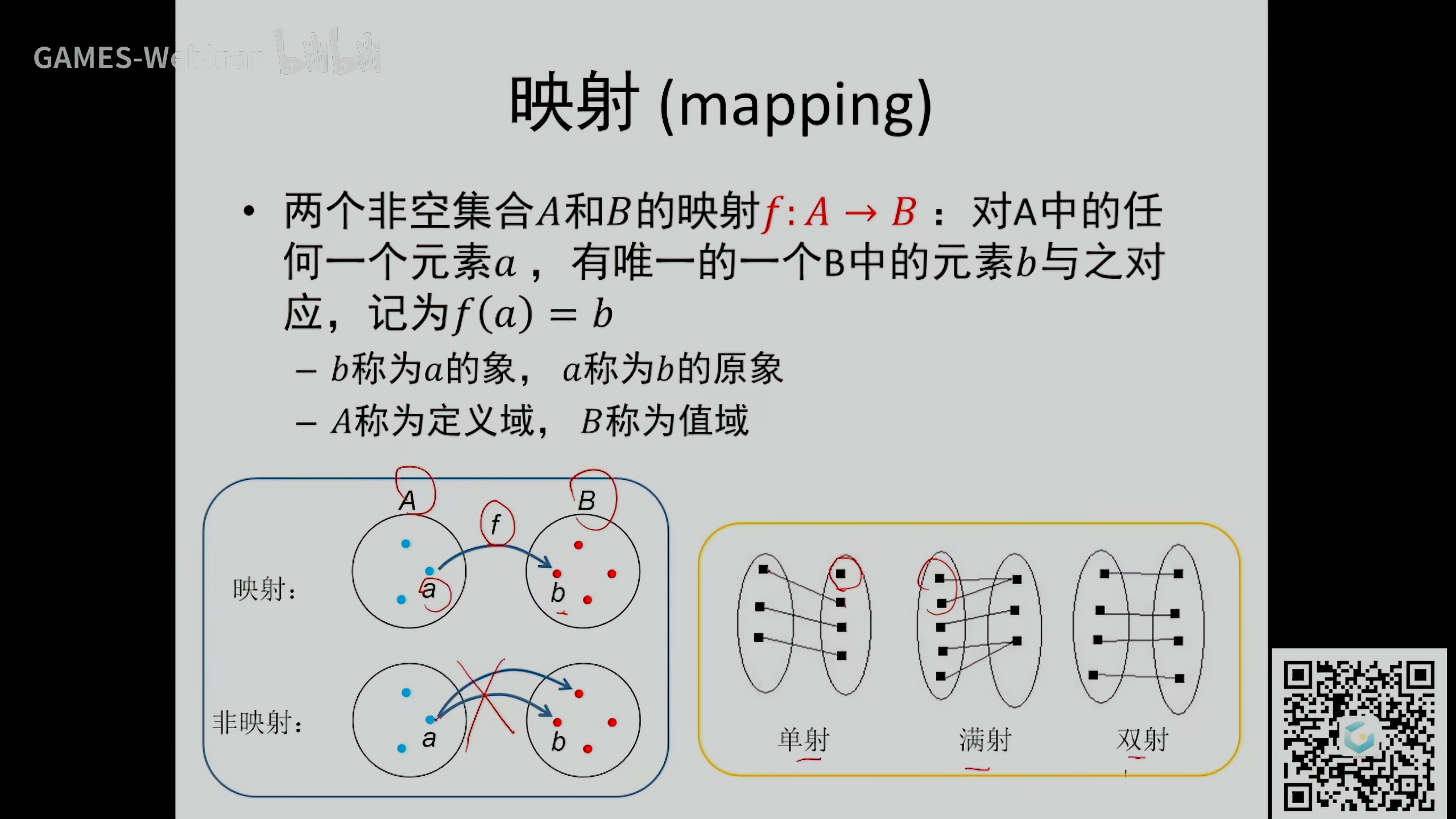
- 一个原象只有对应一个象才是映射
- 每个原象都和一个象一一对应称为单射
- 每个象都有原象对应称为满射
- 同时满足单射和满射称为双射
函数 (Function)
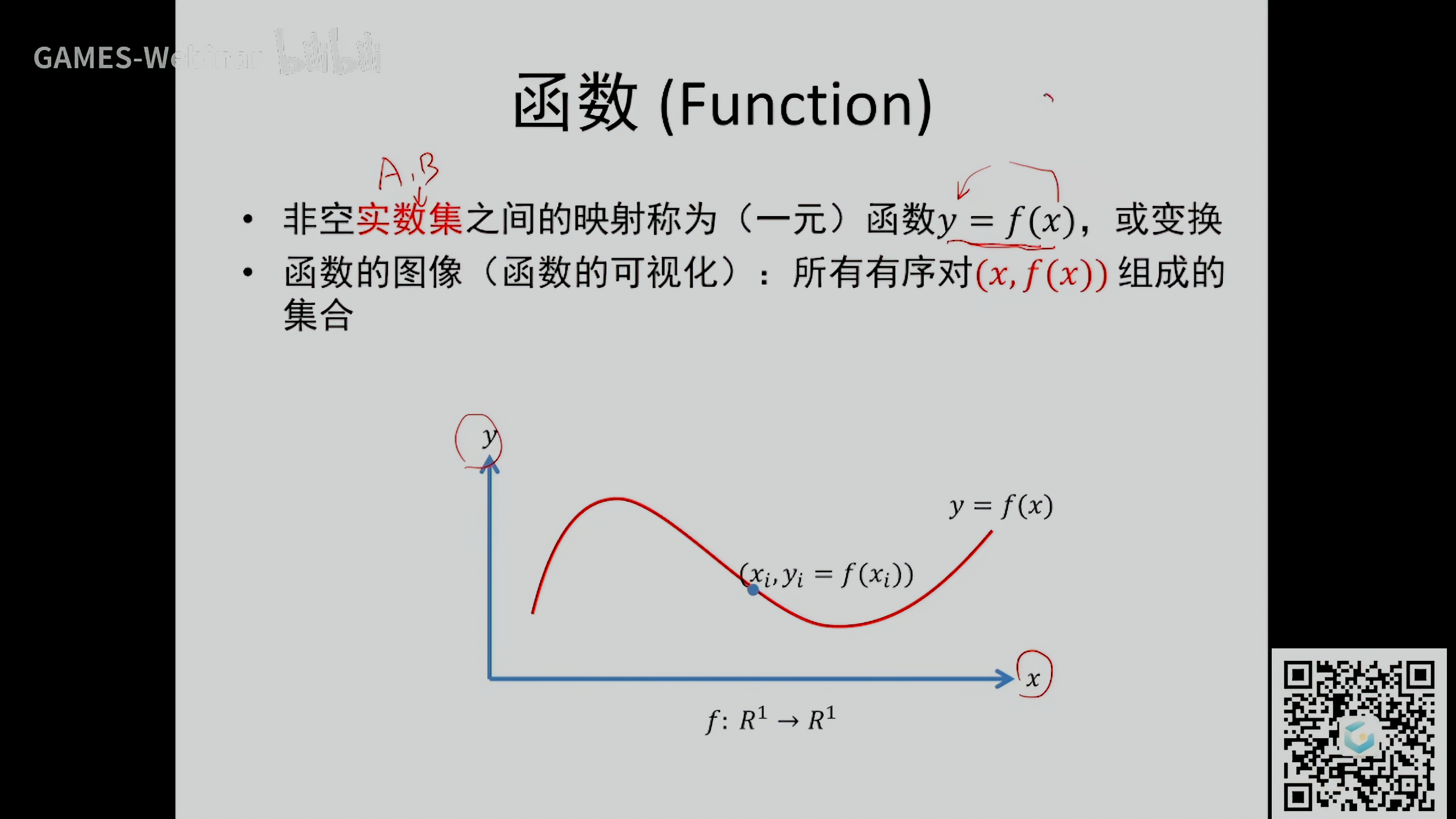
这里特指实数到实数的变换
- 幂函数
- 三角函数
- 对数函数
- 指数函数
- 反三角函数
- ...
函数的集合(函数空间)
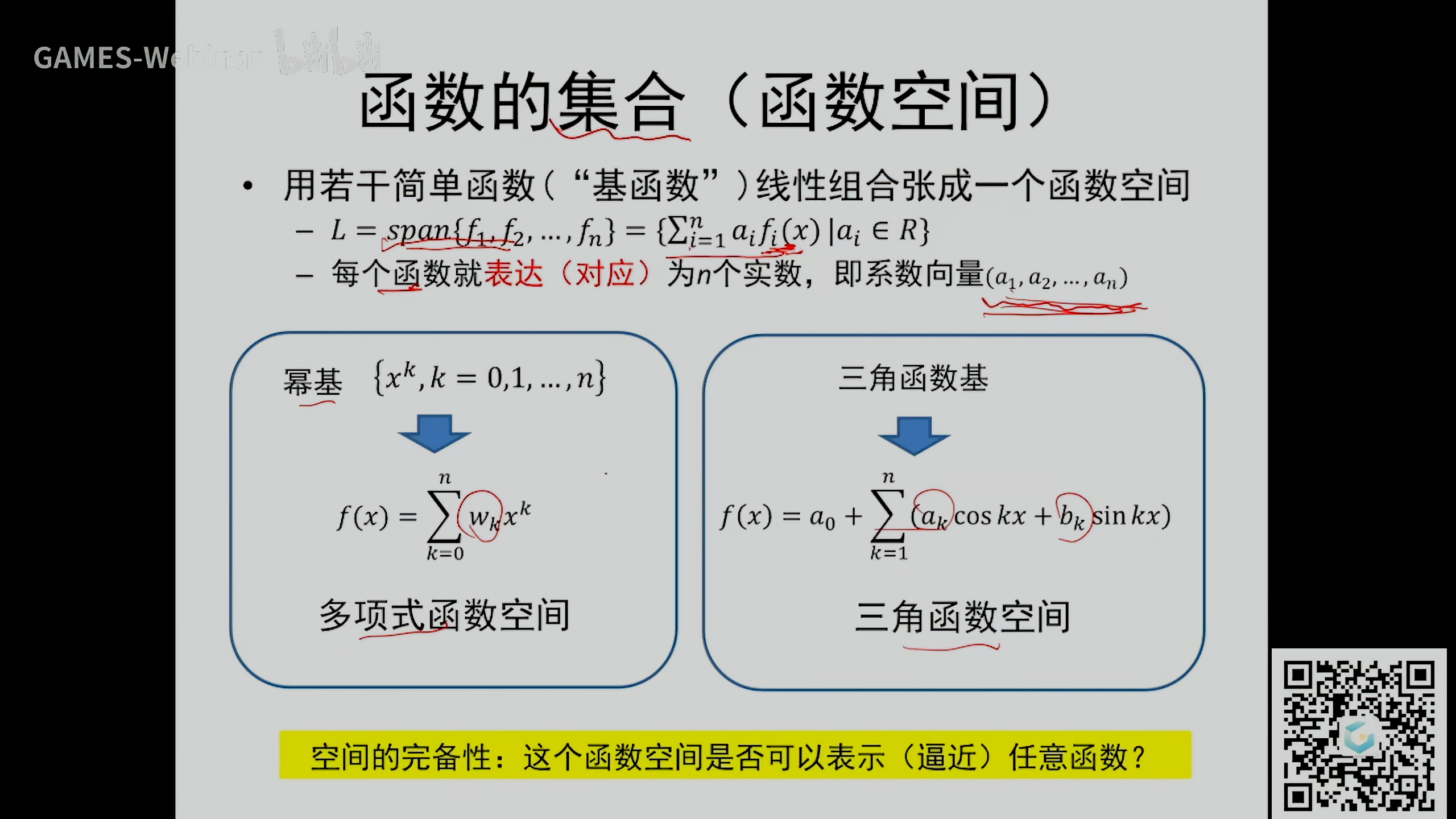
- 用若干个简单函数(“基函数”)线性组合张成一个函数空间
- \(L=span\{f_1,f_2,...,f_n\}=\{\sum_{i=1}^na_if_i(x)\vert a_i\in R\}\)
- 每个函数就表达(对应)\(n\)个实数,即系数向量\(\{a_1,a_2,...,a_n\}\)
空间的完备性:这个函数空间是否可以表示(逼近)任意函数
万能逼近定理:Weierstrass逼近定理
- 定理1:闭区间上的连续函数可用多项式级数一致逼近
- 定理2:闭区间上周期为\(2\pi\)的连续函数可用三角函数级数一致逼近
对于\([a,b]\)上的任意连续函数\(g\),及任意给定的\(\epsilon>0\),必存在\(n\)次代数多项式\(f(x)=\sum_{k=0}^nw_kx^k\),使得\(\underset{x\in[a,b]}{min}\lvert f(x)-g(x)\rvert <\epsilon\)
赋范空间
- 内积诱导函数、距离
- \(<f,g>=\int_a^bf(x)g(x)dx\)
- 度量空间:可度量函数之间的距离
- Lp番薯
- 赋范空间+完备性=巴拿赫空间 Banach
- 内积空间(无限维)+完备性=希尔伯特空间 Hilbert
傅里叶级数
任何一个周期函数都可以写成\(cos\)和\(sin\)的组合
如何求满足要求的函数?
-
大部分的实际应用问题
- 可建模为:找一个映射/变换/函数
- 输入不一样、变量不一样、维数不一样
-
三步
-
到哪找?
- 确定某个函数集合/空间
- 线性函数空间 \(A=span\{B_0(x),...,B_n(x)\}\)
- 多项式函数\(span\{1,x,x^2,...,x^n\}\)
- RBF函数
- 三角函数
- 线性函数空间 \(A=span\{B_0(x),...,B_n(x)\}\)
- 函数表达为
- \(f(x)=\sum_{k=0}^na_kB_k(x)\)
- 求\(n+1\)个系数\((a_0,...,a_n)\) 待定系数
- 确定某个函数集合/空间
-
找哪个?
-
度量哪个函数是最好的
损失函数小则好
-
目标1:加入要求很严格,函数一定要经过给定的点,就要插值(零误差)
- \(y_i=f(x_i),i=0,1,...,n\)
- 联立,求解线性方程组
- \(\sum_{k=0}^{n}a_kB_k(x_i)=y_i,i=0,1,...,n\)
- 求解\((n+1)\times(n+1)\)线性方程组
- \(n\)次拉格朗日插值多项式
- \(\sum_{k=0}^{n}a_kB_k(x_i)=y_i,i=0,1,...,n\)
- 病态问题:系数矩阵条件数高时,求解不稳定
-
目标2:函数尽量靠近数据的(逼近),函数与给定值不一定要严格相等,但要误差最小
-
\(min=\sum_{i=0}^n(y_i-f(x_i))^2\)
-
也可以是绝对值、点到函数的垂足距离
但是这样不好找,不好优化不好求解
-
最小二乘法
-
对各系数求导、得Normal equation 法方程(线性方程组)
- \(AX=b\)
-
问题
-
点多,系数少?
表达能力不够,Underfitting 欠拟合
-
点少,系数多?
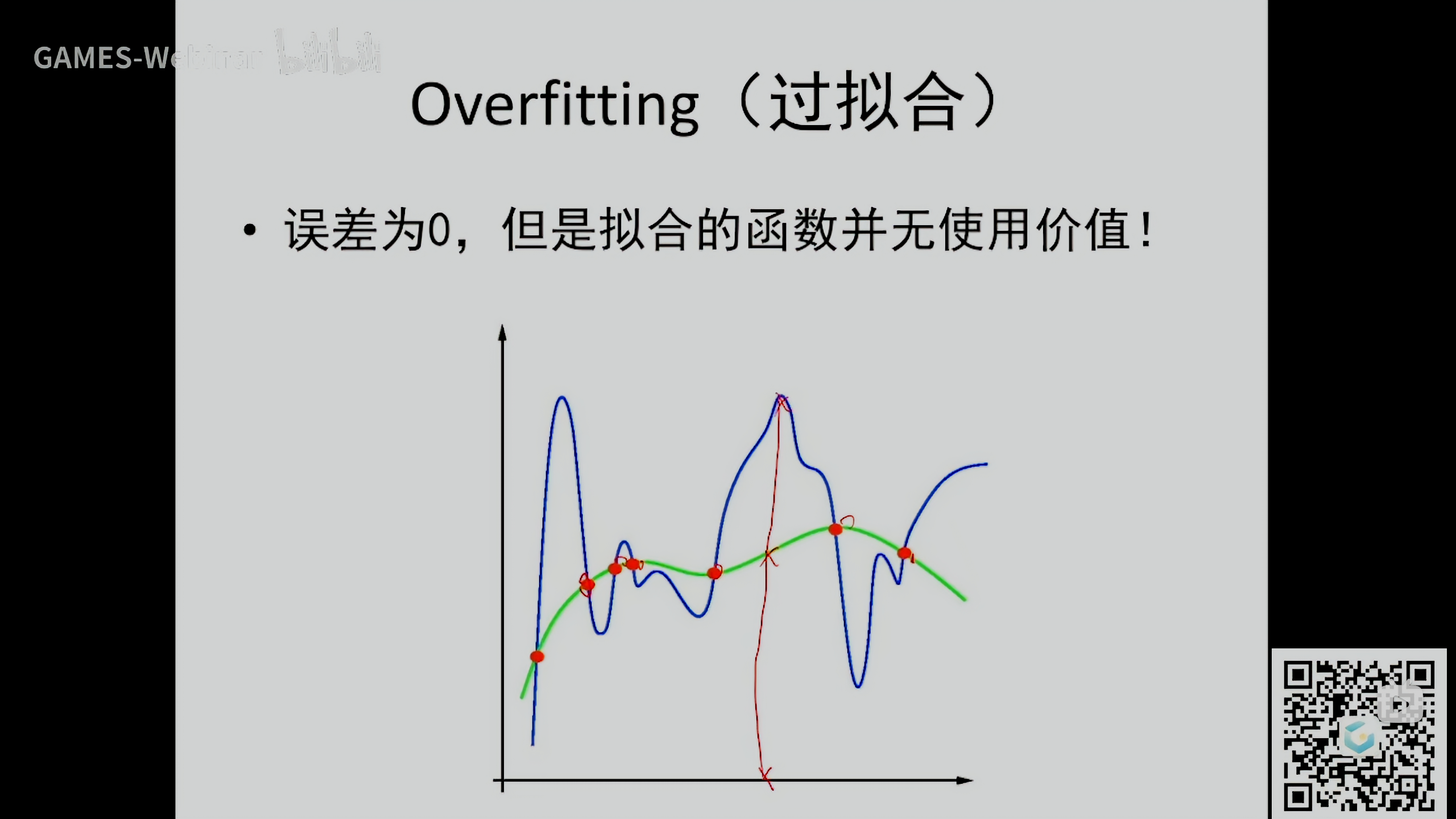
本来是逼近,结果每个点都插值,Overfitting (过拟合)
虽然在给定点的误差为0,但在其他点非常震荡,无使用价值
- 降低过拟合的概率:数据集中90%做拟合,10%不做拟合而做验证
-
需要根据不同的应用与需求,不断尝试(不断”调参“)
-
-
-
-
-
怎么找?
- 求解或优化:不同的优化方法与技巧,既要快、又要好
-
Lagrange插值函数
- 插值\(n+1\)个点、次数不超过\(n\)的多项式是存在且唯一的
- \(n+1\)个变量,\(n+1\)个方程
- \(p_k(x)=\prod_{i\in B_k}\frac{x-x_i}{x_k-x_i}\)
- 插值函数的自由度=未知量个数\(-\)已知量个数
避免过拟合的常用方法
- 数据去噪
- 剔除训练样本中的噪声
- 数据增广
- 增加样本数,或者增加样本的代表性和多样性
- 模型简化
- 预测模型过于复杂,拟合了训练样本中的噪声
- 选用更简单的模型,或者对模型进行裁剪
- 正则约束
- 适当的正则项,比如方差正则项、系数正则项
岭回归正则项
-
选择一个函数空间
-
基函数的线性表达
- \(W=(w_0,w_1,...,w_n)\)
- \(y=f(x)=\sum_{i=-}^nw_iB_i(x)\)
-
最小二乘拟合
- \(\underset{W}{min}\lVert Y-XW\rVert^2\)
-
Ridge regression 岭回归
-
\(\underset{W}{min}\lVert Y-XW\rVert^2+\mu\lVert W\rVert_2^2\)
这里除了误差要最小,还要求系数的模也很小,\(\mu\)是一个权表示比例,这样可以让模型更加稳定
-
-
稀疏学习:稀疏正则化
-
冗余基函数(过完备)
不知道该选哪些基函数,但知道好多函数都跟要求的函数类似,将它们全拿来,这些函数可能过冗余的,甚至是线性相关的(过完备)
-
通过优化来选择合适的基函数
-
系数向量的\(L_0\)模(非0元素个数)尽量小
非0元素越少,0元素就越多
那么也就是希望系数为0的项尽量多,通过这样的优化,就只是选了部分我要的基函数来表达我要的函数
-
挑选(“学习”)出合适的基函数
- \(\underset{\alpha}{min}\lVert Y-XW\rVert^2+\mu\lVert W\rVert_0\)
- \(\underset{\alpha}{min}\lVert Y-XW\rVert^2,\ \rm s.\rm t. \lVert W\rVert_0 \le\beta\)
-
压缩感知
有一些信号\(x\),比如是很高维的,其中只有少量的元素是非0,那么要记录这样的信号需要很长的存储
于是可以通过一个采样矩阵\(\Phi\), 采样矩阵对其进行一个点积(线性乘法)得到一个短的\(y\)
-
已知采样矩阵\(\Phi\)和\(y\),能不能恢复出\(x\)
- 数学上不可能,因为方程个数小于未知数个数,\(x\)有无穷多个
- 但是其中有个解最稀疏,这个解是唯一的
-
那么如果一个信号是稀疏的,通过这样一个优化,就能用很少的存储量存储这个稀疏信号,通过这样的优化反写出\(x\),并且在以概率1收敛,不保证每次都是真解,但是很大概率是真解(解1000次有999次这样),不是一定真解的原因是中间优化存在一些随机量
非函数型的曲线拟合
- Bezier
- B样条
将大问题变为小问题,将复杂函数分成段,每段分别取拟合
函数库
- Eigen


