递归的两种思路
理解递归，首先要理解栈是什么
栈：就是放在桌子上的一叠盘子
官方解释：栈（stack）又名堆栈，是一种运算受限的线性表。仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
人话解释：所谓的栈就是一个线性表。最上面的一个盘子就是栈顶，最下面的一个盘子就是栈底。出栈(pop)就是取走最上面的一个盘子，入栈(push)就是往上面放一个盘子。
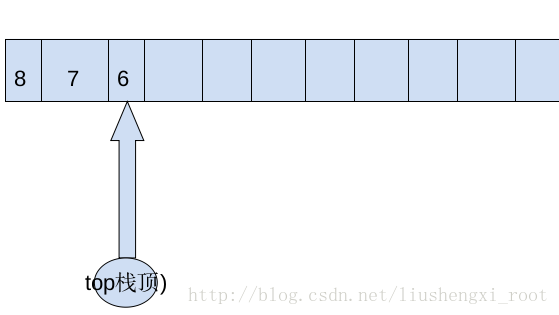
小示例（数组实现的顺序栈）：
#include<stdio.h>
#include<stdlib.h>
#define MAX 30
#define FALSE -1
#define TRUE 0
typedef struct //data structure of stack
{
int data[MAX];
int top ;
}stack;
int init_stack(stack **s) //init the stack
{
*s=(stack *)malloc(sizeof(stack));
if( *s == NULL)
return FALSE ;
(*s)->top= -1;
return TRUE ;
}
int push_stack(stack *s ,int x ) //push x
{
if(s->top == MAX - 1 ) //sure the stack is or not full
{
printf("the stack is full !!\n");
return FALSE;
}
s->data[++s->top]= x ; //frist --
return TRUE;
}
int pop_stack(stack *s ) //pop a element ,return the element's itself
{
if(s->top == -1)
{
printf("the strack is empty !!\n");
return FALSE;
}
else return (s->data[s->top--]);
}
int main(void)
{
stack *s ;
init_stack(&s);
push_stack(s,8);
push_stack(s,7);
push_stack(s,6);
printf("======%5d\n",pop_stack(s)); //6
printf("======%5d\n",pop_stack(s));//7
printf("======%5d\n",pop_stack(s)); //8
push_stack(s,1);
push_stack(s,2);
push_stack(s,3);
printf("======%5d\n",pop_stack(s)); //3
printf("======%5d\n",pop_stack(s)); //2
printf("======%5d\n",pop_stack(s)); //1
printf("======%5d\n",pop_stack(s)); //error ,the stack is empty !!
}简易图解释如下：
顺序：先进后出！！
递归：递归算法是把问题转化为规模缩小了的同类问题的子问题。然后递归调用函数（或过程）来表示问题的解。一个过程(或函数)直接或间接调用自己本身,这种过程(或函数)叫递归过程(或函数).
第一种方法：从大到小，从上到下
示例1：求斐波那契数列的前n项
#include<stdio.h>
int Fibonacci(int n);
int main(void)
{
int n,i,c=0;
printf("Please input the n :\n");
scanf("%d",&n);
for(i=1; i<=n; i++)
{
c = Fibonacci(i);
printf("%d\t",c);
if(i%4==0)
printf("\n");
}
}
int Fibonacci(int n)
{
long int f;
if(n==1 || n==2) //**从小的出口递归退出**
f=1;
else if(n>=3)
f = Fibonacci(n-1) + Fibonacci(n-2);
return f;
}第二种方法：从小到大，从下到上
示例2：使用递归函数，计算100以内的素数之和
#include<stdio.h>
int fun(int n ,int sum )
{
int flag= 0,i;
if(n > 100) //**从大的出口递归退出**
return sum ;
for( i= n- 1;i>1;i--)
{
if(n%i == 0)
{
flag= 1;
break;
}
}
return (flag) ? fun(n+ 1,sum):fun(n+ 1,sum+ n);
}
int main(void)
{
printf("%d\n",fun(2,0));
return 0;
}递归需要注意的地方：
递归算法有四个特性：
（1）必须有可最终达到的终止条件，否则程序将陷入无穷循环
（2）子问题在规模上比原问题小，或更接近终止条件；
（3）子问题可通过再次递归调用求解或因满足终止条件而直接求解；
（4）子问题的解应能组合为整个问题的解。
