栈的应用--马踏棋盘-贪心加栈

问题描述

问题牵引：

1.为什么用数组来作为栈的实现，而不是动态分配，指针加减？
2.directionNext和count数组起了什么作用？是如何实现的？
3.为什么需要while(1)?它是如何起作用的？为什么需要贪心？
4.贪心的思想是如何实现的？
5.核心代码过程的实现是怎样的？

实现代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define ROW 8
#define COL 8
#define maxStep 64  //不管怎样，都是64步

typedef struct {
    int abscissa;  //横坐标
    int ordinate;  //纵坐标
    int direction;  //表示方向
}MyStack;

int ChessBoard[ROW+1][COL+1]={0};  //储存路径的棋盘,可以看出是从1 开始的

//分别有（1 ~ 8）个方向
int HTry1[8]={1, -1, -2, 2, 2, 1, -1, -2};
int HTry2[8]={2, -2, 1, 1, -1, -2, 2, -1};

MyStack PointStack[maxStep];  //结构体数组来作为栈的实现
int top = -1; //栈顶  
int sum = 0;  //一共要计算多少步

int flagOperate = 0; //操作标记
int num = 0;  //记录结果数

void printChessBoard() {
    printf("棋盘路径是:\n");
    for(int i = 1;i <= ROW;i++) {
        for(int j = 1;j <= COL;j++) {
            printf("%5d ", ChessBoard[i][j]);
        }
        printf("\n");
    }
    printf("\n\n");
}
//入栈
void push(int abscissa, int ordinate) {
    ++top;
    PointStack[top].abscissa = abscissa;
    PointStack[top].ordinate = ordinate;
    PointStack[top].direction = -1;  //初始化方向
}

//出栈
void pop() {
    PointStack[top].abscissa = 0;
    PointStack[top].ordinate = 0;
    PointStack[top].direction = -1; //初始化方向
    --top;
}

//标记棋盘
void markChessBoard(int abscissa, int ordinate) {
    ChessBoard[abscissa][ordinate] = top+1;
}

int check(int xx,int yy) //类似于DFS 的检查函数
{
    if(xx > 0 &&  xx <= ROW  && yy > 0 && yy <= COL  &&  ChessBoard[xx][yy] == 0)
        return 1;
    else return 0;
}
void runChessBoard() {
    int xNow, yNow; //当前马所在的坐标
    while(1) {
        if(flagOperate == 1) {
            if(top == maxStep - 1) {
                printChessBoard();
                break;
            }
        }else if(flagOperate == 2 ) {
            if(top == maxStep - 1){
                num++;
                printf("%d \n\n", num);
                printChessBoard();
            }
        }
        if(sum != 0  && num == sum )
            break;
        xNow = PointStack[top].abscissa;
        yNow = PointStack[top].ordinate;

        //对下面八个方向重新排序，出口最少的优先
        int count[8]={0};
        for(int i = 0;i < 8;i++) {
            int xNext = xNow, yNext = yNow;
            xNext += HTry1[i];
            yNext += HTry2[i];
            if(check(xNext,yNext)) {
                for(int j = 0;j < 8;j++) {
                    int xNextNext = xNext, yNextNext = yNext;
                    xNextNext += HTry1[j];
                    yNextNext += HTry2[j];
                    if(check(xNextNext,yNextNext)) {
                        count[i]++;  //count 数组保存了下一步（8个方向）的下一步有多少步
                    }
                }
            }
        }
        //对方向进行排序，实际要走的方向记录在directionNext中
        int directionNext[8] = {0};
        int temp = 9;
        int  k = 0;
        for(int i = 0;i < 8;i++) {
            temp = 9;
            for(int j = 0;j < 8;j++) {
                if(count[j]<temp){
                    directionNext[i] = j;
                    temp = count[j];
                    k = j;
                }
            }
            count[k] = 9;
        }
        //走下一步
        int direnow = 0;  //通过directionNext数组的牵引找到那个下一步最少的点进行踏走
        for(direnow = PointStack[top].direction + 1 ; direnow <  8  ; direnow++) {
            int xRealNext = xNow, yRealNext = yNow;
            xRealNext += HTry1[directionNext[direnow]];
            yRealNext += HTry2[directionNext[direnow]];
            PointStack[top].direction += 1;
                if(check(xRealNext,yRealNext)) {
                push(xRealNext, yRealNext);
                markChessBoard(xRealNext, yRealNext);
                break;
            }
        }
        //判断无路可走出栈
        if(PointStack[top].direction >= 7) {
            int x, y;
            x = PointStack[top].abscissa;
            y = PointStack[top].ordinate;
            ChessBoard[y][x] = 0; //棋盘标记取消
            pop();
        }
    }
}
void InitStartPoint() {
    int x, y;
    //输入起始坐标点
    printf("请输入起始点（x，y）(1~~8):");
    scanf("%d%d", &x, &y);
    printf("请输入你的选择：\n  1.找出一个结果\n  2.找出所有结果(几乎不可能)\n  3.找多少个解  \n 输入:");
    scanf("%d", &flagOperate);

    while( x > ROW || x <  1 || y > COL || y < 1  || flagOperate < 1 ||  flagOperate > 3) {    //进入while 就是输入错误的处理
        if((x > ROW||x  <  1)&&(y > COL || y  < 1 )) {
            printf("输入的坐标超出范围，请重新输入（1~8）：");
            scanf("%d%d", &x, &y);
        }else if(flagOperate < 1 || flagOperate >  3) {
            printf("输入错误，请重新输入：\n");
            printf("请输入你的选择：\n  1.找出一个结果\n  2.找出所有结果(几乎不可能)\n   3.找多少个解  \n 输入:");
            scanf("%d", &flagOperate);
        }
    }
    if(flagOperate == 3){  //找多少个解，按照所有来计算，欺骗用户
        printf("请输入所找的解的数量：( > 0)");
        scanf("%d",&sum);
        flagOperate = 2;
    }
    //入首栈
    push(x, y);
    markChessBoard(x, y);
}
int main(void) {
    InitStartPoint();
    clock_t start,finish; //开始结束时间
    double duration;  //运行用时
    start = clock();
    runChessBoard();
    finish = clock();
    duration = (double) (finish - start) / CLOCKS_PER_SEC;
    printf("运行用时: %f second\n", duration);
}

运行截图：

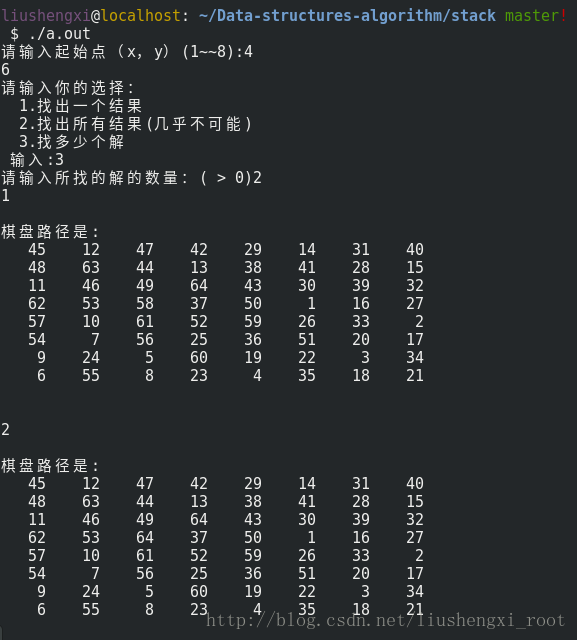
小枝小解：

1.为什么用数组来作为栈的实现，而不是动态分配，指针加减？因为数组含有自然下标，第几步可以直接等于 top+1 ；用指针的话 ，还必须用 top-base 来计算一下，带来了一定的麻烦。

2.directionNext和count数组起了什么作用？是如何实现的？先不着急,让我们来看几段小示例,你就会知道了。

(1).(count数组)我们将文中的代码进行下面的改动:

        xNow = PointStack[top].abscissa;
        yNow = PointStack[top].ordinate;
        //对下面八个方向重新排序，出口最少的优先
        int count[8]={0};
        for(int i = 0;i < 8;i++) {
            int xNext = xNow, yNext = yNow;
            xNext += HTry1[i];
            yNext += HTry2[i];

            printf("计算出来的下一步的坐标是:");

            printf("%5d%5d \n",xNext,yNext);
            if(check(xNext,yNext)) {
                for(int j = 0;j < 8;j++) {
                    int xNextNext = xNext, yNextNext = yNext;
                    xNextNext += HTry1[j];
                    yNextNext += HTry2[j];
                    if(check(xNextNext,yNextNext)) {
                        count[i]++;  //count 数组保存了下一步（8个方向）的下一步有多少步
                    }
                }
            }
        }
        printf("count 数组是:\n");
        for(int j = 0 ;j< 8;j++)
            printf("%4d",count[j]);
        printf("\n\n");
        exit(1);

运行结果：

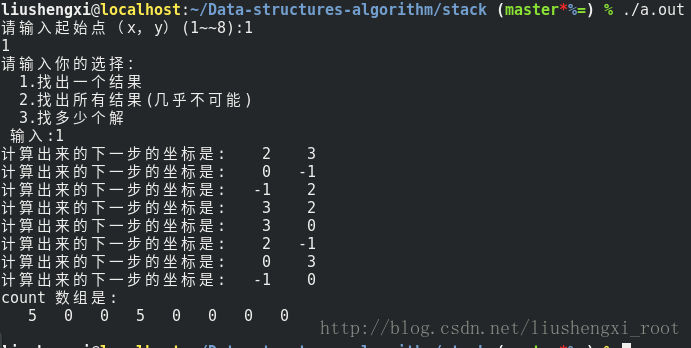
分析：

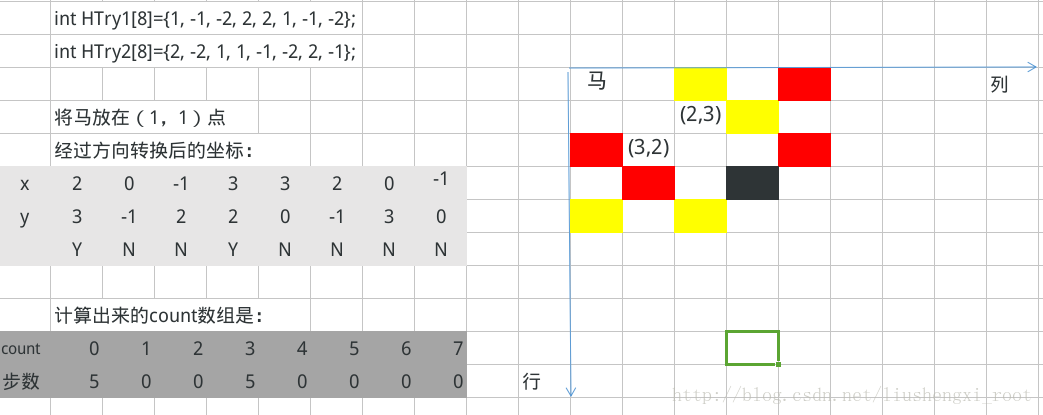
图中黄色表示（3，2）这一点能走的地方，红色表示（2，3）这一点能走的地方，黑色代表重合。可见都是5个地方。那么count数组中其实就是存储了一个方向上的下一步可走的步数

(2).（directionNext数组） 示例代码:

#include<stdio.h>
int main(void)
{
    int count[8]={3,2,5,1,4,7,6,9};
    int i ;
        int directionNext[8] = {0};
        int temp = 9;
        int  k = 0;
        for(int i = 0;i < 8;i++) {
            temp = 9;
            for(int j = 0;j < 8;j++) {
                if(count[j]<temp){
                    directionNext[i] = j;
                    temp = count[j];
                    k = j;
                }
            }
            count[k] = 9;
        }
    for(i= 0;i< 8;i++)
    {
        printf("count下标：%d : %d \n",i,count[i]);
    }
    for(i= 0;i< 8;i++)
    {
        printf("directionNext下标：%d : %d \n",i,directionNext[i]);

    }
}

运行结果：

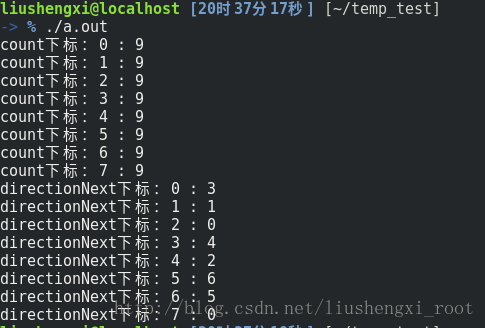
分析：由结果可以看到，directionNext 中是存储了count数组中从小到大排列之后的下标

3.为什么需要while(1)?它是如何起作用的？为什么需要贪心？因为如果要求所有解的话，就需要用到它。如果已经找到一个方法，就进行下一步，判断无路可走， 又出栈，进行下一个方向的寻找，即可满足找多少条路的要求。

4.贪心的思想是如何实现的？哪一个点的下一步少，就选哪一个先走，就能达到优化的需求

PS: 其实这个程序的效率还不是我想要的，因为这个程序去计算10万条路径的话，还是需要一定的时间的（30多秒吧好像是），而我想要的是在一秒中之内解决。在网上搜到一篇文章，贴出链接：文章但是无奈能力有限，没有改造出来，如果有人愿意搞搞，欢迎联系我（QQ：1589570280）

参考资料：http://www.jianshu.com/p/6c185f290e10