运算符重载的几个小例子
0.重载运算符时,*必须首先决定是将其声明为类的成员函数(有一个this指针)还是非成员函数!!!* 一般有下面的这样一些规则:
必须这样做的:
- =,[ ],( ) , -> 必须是成员函数
- 希望为类自定义IO运算符时 ,输入 >> 和输出 << 运算符必须是友元非成员函数
按你的想法和要求做的:
- += ,-= 等复合赋值运算符之类的一般来讲是成员,但并非必须,与 = 号完全不同.
- 改变对象状态的运算符或者是与给定类型密切相关的运算符,如:递增(++),递减(–)和 (*) 解引用运算符,通常来讲是成员函数
- 具有对称性的运算符(int + double)可能转换为任意一端的运算对象,例如:算术(+ - * / ),相等性(==),关系(< > != )和位运算符等,通常为非成员函数
不应该被重载的运算符:
1. ,(逗号)
2. & (取地址)
3. || (逻辑或)
4. && (逻辑与)
当我们把运算符定义为成员函数时,他的左侧运算对象必须是运算符所属类的一个对象
1.坐标 :
#include <iostream>
using namespace std;
/**
* 定义Coordinate类
* 数据成员:m_iX,m_iY
* 成员函数:构造函数
* 重载--运算符,重载+运算符
*/
class Coordinate // 坐标
{
public:
Coordinate(int x, int y)
{
m_iX = x ;
m_iY = y ;
}
// 前置--运算符重载
Coordinate &operator--( ){
--m_iX ;
--m_iY ;
return *this ;
}
// 后置--运算符重载
Coordinate operator--(int ){
Coordinate temp(*this) ;
this->m_iX-- ;
this->m_iY-- ;
return temp ;
}
// +号运算符重载
Coordinate operator+(Coordinate &temp2){
int x = this->m_iX + temp2.m_iX ;
int y = this->m_iY + temp2.m_iY ;
return Coordinate(x,y);
}
public:
int m_iX;
int m_iY;
};
int main(void)
{
Coordinate coor1(1, 3);
Coordinate coor2(2, 4);
Coordinate coor3(0, 0);
coor1--; //(0,2)
--coor2; //1,3
coor3 = coor1 + coor2; //1,5
cout << coor3.m_iX << endl;
cout << coor3.m_iY << endl;
return 0;
}重点与难点:前置减减与后置减减的重载
// 前置--运算符重载
Coordinate &operator--( ){
--m_iX ;
--m_iY ;
return *this ;
}
// 后置--运算符重载
Coordinate operator--(int ){ //好象是必须要写为int 参数
Coordinate temp(*this) ;
this->m_iX-- ;
this->m_iY-- ;
return temp ;
}执行结果:
2.复数的加减乘除运算 :
#include<iostream>
using namespace std;
//复数
class plural{
public:
plural() = default ;
plural(int a,int b):Real_component(a),Imaginary_part(b){}
plural operator+(plural &) ; // 重载 + 号
plural operator-(plural &) ; // 重载 - 号
plural operator*(plural &) ; // 重载 * 号
void print() ;
private:
int Real_component ; //实部
int Imaginary_part ; //虚部
};
plural plural::operator+(plural &a )
{
plural temp ;
temp.Real_component = a.Real_component + Real_component ;
temp.Imaginary_part = a.Imaginary_part + Imaginary_part ;
return temp ;
}
plural plural::operator-(plural &b )
{
int x = Real_component - b.Real_component ;
int y = Imaginary_part - b.Imaginary_part ;
return plural(x,y);
}
plural plural::operator*(plural &c )
{
int x = c.Real_component *Real_component - c.Imaginary_part*Imaginary_part ;
int y = c.Real_component * Imaginary_part + c.Imaginary_part * Real_component ;
return plural(x,y) ;
}
void plural::print()
{
if(Imaginary_part < 0)
cout << Real_component << Imaginary_part << "i " << endl ;
else
cout << Real_component << "+" << Imaginary_part << "i " << endl ;
}
int main(void)
{
plural f1(1,-4),f2(-1,9) ,add ;
cout << "f1 == " ;
f1.print();
cout << "f2 == " ;
f2.print();
add = f1 +f2 ;
cout << "f1 + f2 == " ;
add.print() ;
plural sub = f1 - f2 ;
cout << "f1 - f2 == " ;
sub.print();
plural mul = f1 * f2 ;
cout << "f1 * f2 == " ;
mul.print();
return 0;
}
执行结果:
3.有理数的加减乘除运算:
#include<iostream>
#include<cmath>
using namespace std ;
// 有理数
class RationalNumber{
public:
RationalNumber() = default;
RationalNumber(int a,int b):molecular(a),denominator(b){}
RationalNumber operator + (RationalNumber &);
RationalNumber operator - (RationalNumber &);
RationalNumber operator * (RationalNumber &);
RationalNumber operator / (RationalNumber &);
void print() ;
private:
RationalNumber &reduction();
int molecular ; //分子
int denominator ; //分母
};
//考虑分母为零和化简
int gcd(int a,int b) //找到最大公约数
{
return a%b ?gcd(b,a%b):b; //gcd 算 法
}
RationalNumber &RationalNumber::reduction() //化简函数
{
if(denominator < 0 )
{
molecular = -molecular ;
denominator = -denominator ;
}
int temp = gcd(abs(molecular),abs(denominator));
molecular /= temp ;
denominator /= temp ;
return *this ; //改变调用对象
}
RationalNumber RationalNumber:: operator + (RationalNumber &rhs)
{
int a,b,c,d ;
a = molecular ;
b= denominator ;
c= rhs.molecular ;
d= rhs.denominator ;
return RationalNumber(a*d+b*c,b*d);
}
RationalNumber RationalNumber:: operator - (RationalNumber &rhs)
{
int a,b ;
int multiy ;
multiy = rhs.denominator * denominator ;
a = molecular* rhs.denominator ;
b= denominator * rhs.molecular ;
return RationalNumber(a-b,multiy);
}
RationalNumber RationalNumber:: operator * (RationalNumber &rhs)
{
int a,b,c,d ;
a = molecular ;
b= denominator ;
c= rhs.molecular ;
d= rhs.denominator ;
return RationalNumber(a*c,b*d);
}
RationalNumber RationalNumber:: operator / (RationalNumber &rhs)
{
int a,b,c,d ;
a = molecular ;
b= denominator ;
c= rhs.molecular ;
d= rhs.denominator ;
return RationalNumber(a*d,b*c);
}
void RationalNumber::print()
{
reduction();
cout << molecular << "/ " << denominator << endl ;
}
int main(void)
{
RationalNumber t1(8,-16),t2(2,3) ,t3 ;
cout << "t1 == " ;
t1.print() ;
cout << "t2 == " ;
t2.print() ;
cout << "t1 + t2 == " ;
t3 = t1 + t2 ;
t3.print() ;
cout << "t1 - t2 == " ;
t3 = t1 - t2 ;
t3.print() ;
cout << "t1 * t2 == " ;
t3 = t1 * t2 ;
t3.print() ;
cout << "t1 / t2 == " ;
t3 = t1 / t2 ;
t3.print() ;
cout << endl ;
return 0;
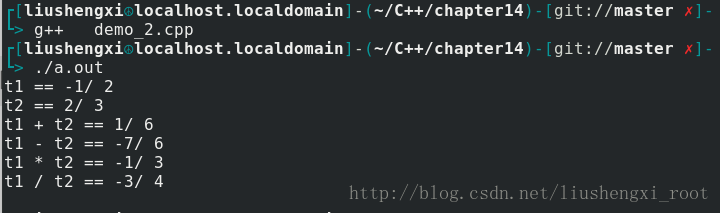
}执行结果: