贪心算法
贪心算法有很多经典的应用,比如霍夫曼编码(Huffman Coding)、Prim 和 Kruskal 最小生成树算法、还有 Dijkstra 单源最短路径算法。最小生成树算法和最短路径算法我们后面会讲到,所以我们今天讲下霍夫曼编码,看看它是如何利用贪心算法来实现对数据压缩编码,有效节省数据存储空间的
什么是贪心算法?
关于贪心算法,我们先看一个例子。
假设我们有一个可以容纳 100kg 物品的背包,可以装各种物品。我们有以下 5 种豆子,每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大,我们如何选择在背包中装哪些豆子?每种豆子又该装多少呢?

实际上,这个问题很简单,就是按照单价从大到小来装就行了,对吧?
以上本质上借助的就是贪心算法。结合这个例子,我总结一下贪心算法解决问题的步骤,我们一起来看看。
- 第一步,当我们看到这类问题的时候,首先要联想到贪心算法:针对一组数据,我们定义了限制值和期望值,希望从中选出几个数据,在满足限制值的情况下,期望值最大
类比到刚刚的例子,限制值就是重量不能超过 100kg,期望值就是物品的总价值。这组数据就是 5 种豆子。我们从中选出一部分,满足重量不超过 100kg,并且总价值最大。
- 第二步,我们尝试看下这个问题是否可以用贪心算法解决:每次选择当前情况下,在对限制值同等贡献量的情况下,对期望值贡献最大的数据。
类比到刚刚的例子,我们每次都从剩下的豆子里面,选择单价最高的,也就是重量相同的情况下,对价值贡献最大的豆子。
- 第三步,我们举几个例子看下贪心算法产生的结果是否是最优的。大部分情况下,举几个例子验证一下就可以了。严格地证明贪心算法的正确性,是非常复杂的,需要涉及比较多的数学推理。
实际上,用贪心算法解决问题的思路,并不总能给出最优解。
我来举一个例子。在一个有权图中,我们从顶点 S 开始,找一条到顶点 T 的最短路径(路径中边的权值和最小)。贪心算法的解决思路是,每次都选择一条跟当前顶点相连的权最小的边,直到找到顶点 T。按照这种思路,我们求出的最短路径是 S->A->E->T,路径长度是 1+4+4=9。
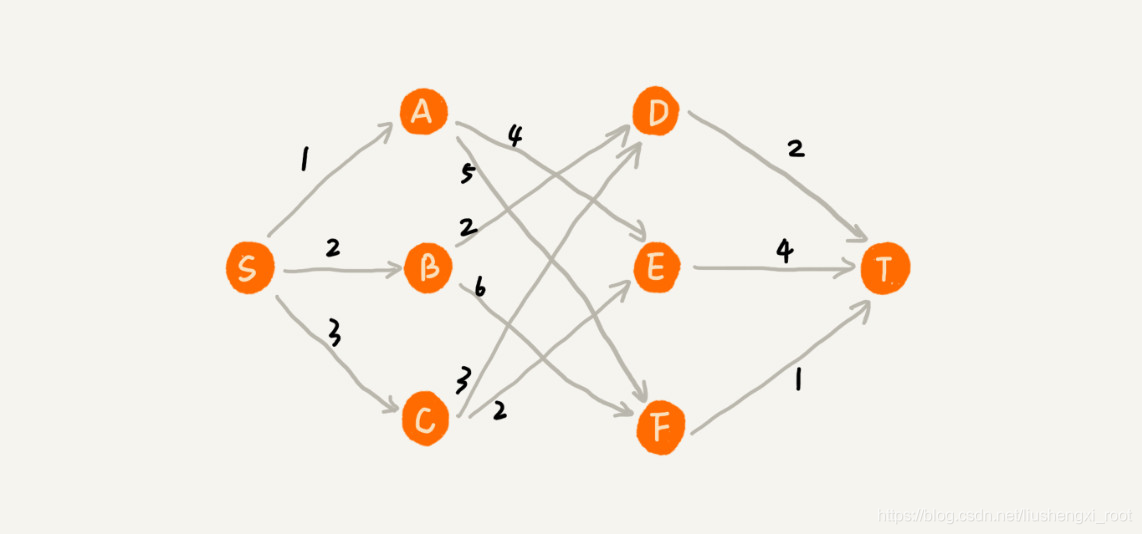
很明显,这不是最短路径,最短路径是S->B->D->T,那么这是为什么呐?
在这个问题上,贪心算法不工作的主要原因是,前面的选择,会影响后面的选择。如果我们第一步从顶点 S 走到顶点 A,那接下来面对的顶点和边,跟第一步从顶点 S 走到顶点 B,是完全不同的。所以,即便我们第一步选择最优的走法(边最短),但有可能因为这一步选择,导致后面每一步的选择都很糟糕,最终也就无缘全局最优解了。
贪心算法实战分析
1. 分发糖果(Leetcode题目)
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
示例 1:
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
贪心思想分析:期望是让糖果数目最小,限制就是那两个条件,如果下一个要大,那自然最好的选择就是多给一个糖果最好,所以在这里我们先不考虑其他的,就给他一个糖果就好.这样遍历过去主要是无法处理1,2,3,3,2,1这类数据,那么再逆着遍历贪心就行了(这个比较难想到)
class Solution {
public:
int candy(vector<int>& rat) {
//贪心
int len = rat.size();
vector<int> candy(len,1);
candy[0]=1;
for(int i=0 ;i< len-1 ;i++){
if(rat[i+1] > rat[i] )
candy[i+1] =candy[i]+1;
}
//逆着贪心
for(int i=len-1 ;i > 0;i--){
if(rat[i-1] > rat[i] && candy[i-1] <=candy[i])
candy[i-1] = candy[i]+1;
}
int result = 0 ;
for(auto i:candy)
result+=i;
return result;
}
};
2. 2. 钱币找零(有面值为1的可以"考虑"贪心,没有就 DP )
这个问题在我们的日常生活中更加普遍。假设我们有 1 元、2 元、5 元、10 元、20 元、50 元、100 元这些面额的纸币,它们的张数分别是 c1、c2、c5、c10、c20、c50、c100。我们现在要用这些钱来支付 K 元,最少要用多少张纸币呢?
在生活中,我们肯定是先用面值最大的来支付,如果不够,就继续用更小一点面值的,以此类推,最后剩下的用 1 元来补齐。
在贡献相同期望值(纸币数目)的情况下,我们希望多贡献点金额,这样就可以让纸币数更少,这就是一种贪心算法的解决思路。直觉告诉我们,这种处理方法就是最好的。实际上,要严谨地证明这种贪心算法的正确性,需要比较复杂的、有技巧的数学推导,我不建议你花太多时间在上面,不过如果感兴趣的话,可以自己去研究下。
3. 3. 区间覆盖
假设我们有 n 个区间,区间的起始端点和结束端点分别是 [l1, r1],[l2, r2],[l3, r3],……,[ln, rn]。我们从这 n 个区间中选出一部分区间,这部分区间满足两两不相交(端点相交的情况不算相交),最多能选出多少个区间呢(这是期望)?

这个问题的处理思路稍微不是那么好懂,不过,我建议你最好能弄懂,因为这个处理思想在很多贪心算法问题中都有用到,比如任务调度、教师排课等等问题。 (这个应该和动态规划放在一起比较一下)
这个问题的解决思路是这样的:我们假设这 n 个区间中最左端点是 lmin,最右端点是 rmax。这个问题就相当于,我们选择几个不相交的区间,从左到右将 [lmin, rmax] 覆盖上。我们按照起始端点从小到大的顺序对这 n 个区间排序。
我们每次选择的时候,左端点跟前面的已经覆盖的区间不重合的,右端点又尽量小的,这样可以让剩下的未覆盖区间尽可能的大,就可以放置更多的区间。这实际上就是一种贪心的选择方法。

leetcode题目:
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
class Solution
{
public:
int eraseOverlapIntervals(vector<Interval> &vals)
{
if(vals.size() == 0 )
return 0;
//期望是移除的数量最小,那么还是找最短的区间去覆盖整个区间即可
sort(vals.begin(), vals.end(), [](const Interval &a, const Interval &b) {
return a.start < b.start;
});
int result = 0;
stack<Interval> ss ;
ss.push(vals[0]);
for (int i = 1; i < vals.size(); i++)
{
Interval tmp = ss.top();
if (vals[i].end < tmp.end){ //前一个比当前的区间长
result+=1;
ss.pop();//把上一个淘汰,下面自然会push进去
}
else if(vals[i].start < tmp.end && vals[i].end >= tmp.end){ //区间相交
result += 1;
continue;//不用push,直接淘汰
}
//满足所有条件 push
ss.push(vals[i]);
}
return result;
}
};
4. 如何实现Huffman编码?
霍夫曼编码不仅会考察文本中有多少个不同字符,还会考察每个字符出现的频率,根据频率的不同,选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法,来进一步增加压缩的效率。如何给不同频率的字符选择不同长度的编码呢?根据贪心的思想,我们可以把出现频率比较多的字符,用稍微短一些的编码;出现频率比较少的字符,用稍微长一些的编码。
5. 在一个非负整数 a 中,我们希望从中移除 k 个数字,让剩下的数字值最小,如何选择移除哪 k 个数字呢?
搞不懂他要干个啥!!!!
6. 假设有 n 个人等待被服务,但是服务窗口只有一个,每个人需要被服务的时间长度是不同的,如何安排被服务的先后顺序,才能让这 n 个人总的等待时间最短?
一直时间最短的先服务(堆)



