数模——相关性分析

相关性分析

基本变量：

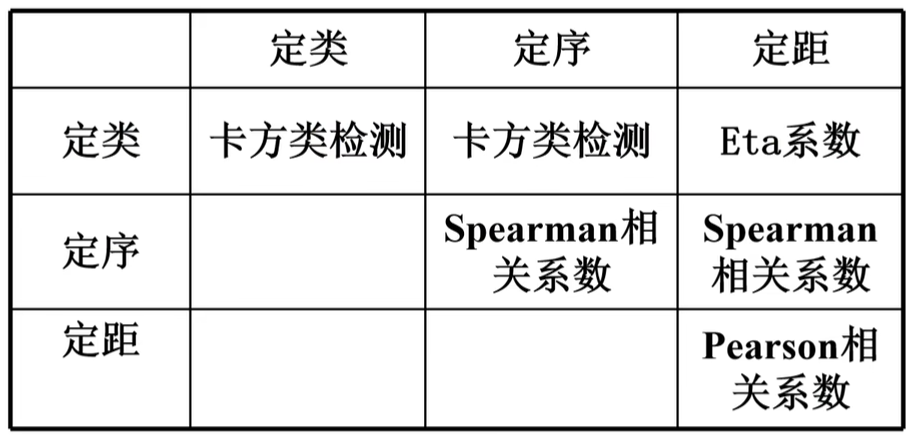
定类、定序、定距、定比是统计学中对变量的常见分类方式，它们描述了不同类型变量的特征和测量尺度，以下是它们之间的区别：

1. 定类（Nominal）变量：

定类变量是指用于标识或分类个体或事物的变量，其取值仅表示不同的类别或分类，没有顺序或大小的含义。例如，性别（男、女）、血型（A、B、AB、O）等就属于定类变量。定类变量通常用符号或名称来表示。

2. 定序（Ordinal）变量：

定序变量是指具有一定顺序但无法测量其差异大小的变量。它们表示的是相对的顺序关系，而不是具体的数值大小。例如，教育程度（小学、中学、高中、大学）可以看作是一个定序变量。虽然它们有一定的顺序，但我们无法确定每个级别之间的具体差异。

3. 定距（Interval）变量：

定距变量是指具有一定的顺序和可以测量差异大小的变量，但没有绝对的零点。定距变量表示了变量之间的固定间隔，但没有一个真正意义上的“零”。例如，温度的摄氏度就是一个定距变量，0°C并不表示完全没有温度，只能说明相对于绝对零点的温度差异。

4. 定比（Ratio）变量：

定比变量是指具有一定顺序、可以测量差异大小，并且具有绝对零点的变量。定比变量具有绝对零点的意义是零点表示完全没有该属性或现象。例如，年龄、身高、重量都是定比变量，它们具有具体的数值大小，并且可以进行比较和计算。

总之，定类、定序、定距和定比是描述不同类型变量的方式，它们在测量尺度和所表示的信息的程度上具有不同的特征。了解变量的类型有助于我们选择适当的统计分析方法。

 

分析方法：

皮尔逊系数法 (Pearson相关系数)：

• 是统计学中运用最为广泛的一种相关程度分析统计量，检验是常用 t 统计量 (其中统计量 t 应当服从t (n-2) ，n为特征总量)。
• 适用条件：
  • 两个变量均应由测量得到的连续变量
  • 两个变量应该均来自正态总体，或接近正态的单峰对称分布
  • 变量必须是成对的数据
  • 两个变量之间存在线性关系
  • 两个变量是定距、定比类型的变量
• 相关性系数 r ：
• 统计量 t ：大于上 a / 2分位点即为合理
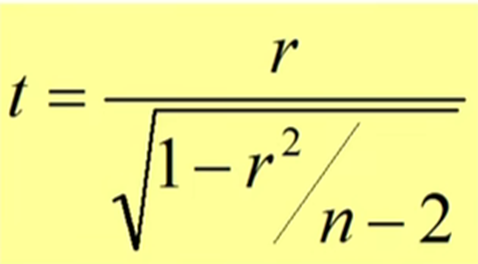
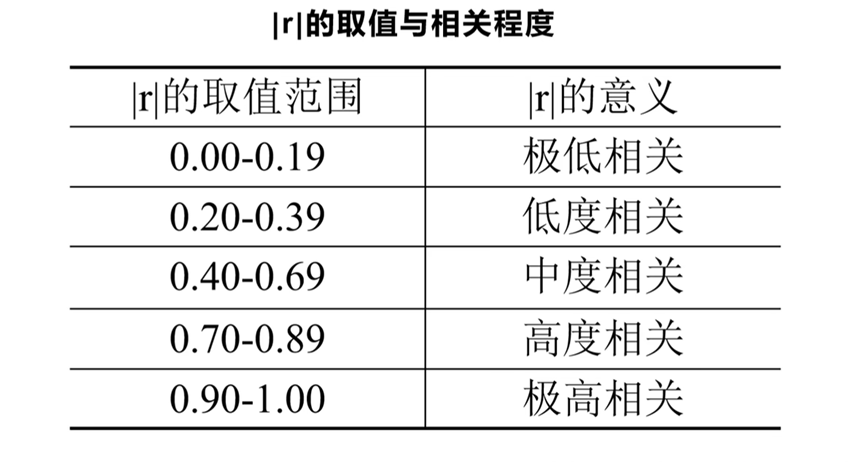
• 相关程度描述与区分：

Spearman相关性系数法：

• 适用于度量定序变量与定序变量之间的的相关性分析。
• 计算的具体步骤：

1. 将变量按大小次序排序，从大到小排序
2. 计算（赋予）等级次序，为每一个排序后的数据分配一个等级次序，最小值的等级为1，此后一次加1
3. 计算等级差 d_i 、相关系数 r_s 、检验统计量 t 
4. 分析相关性

• 相关性系数 r_s ：

   

• 其中 d_i 表示 ( x_i - y_i )²。
• 统计量 t ：大于上 a / 2分位点即为合理，使用统计量 t 进行检验建议 n > 20。
• 

其他：