数学基础——矩阵的点乘与叉乘

数学基础——矩阵的点乘与叉乘

点乘
  • 简而言之就是矩阵各对应元素相乘。
  • 需满足乘数矩阵和被乘数矩阵的行向量或列向量相等，或两者同时相等。

举个栗子：

1.

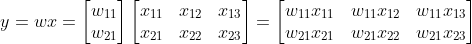
2.

代码描述：

 1 A = np.array([[1],[2]])
 2 B = np.array([[1,2,4],[1,4,5]])
 3 C = np.array([[1,2,3],[4,5,6]])
 4  
 5 X = A*B
 6 array([[ 1,  2,  4],
 7        [ 2,  8, 10]])
 8  
 9 X == np.multiply(A,B)
10 array([[ True,  True,  True],
11        [ True,  True,  True]])
12  
13 Y = B*C
14 array([[ 1,  4, 12],
15        [ 4, 20, 30]])
16 Y == np.multiply(B,C)
17 array([[ True,  True,  True],
18        [ True,  True,  True]])

 

需要点出的是：

当矩阵A和矩阵B的维度相同时，矩阵点乘即为哈达玛积（Hadamard Product/Point-wise Product/Element-wise Product/Element-wise Multiplication），如下图所示：

总结：

 numpy库中可使用运算符*或multiply函数计算。

向量点乘的几何意义是：向量x在向量y方向上的投影再与向量y的乘积，能够反应两个向量的相似度。向量点乘结果大，两个向量越相似。

叉乘
  • 就是我们熟知的矩阵乘法。
  • 中间相同留两边。

举个栗子：

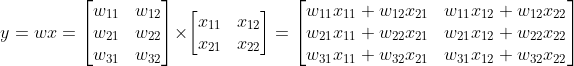
代码描述：

 1 A = np.array([[1,2],[3,4],[1,5]])
 2 B = np.array([[1,2],[2,1]])
 3  
 4 A@B
 5 array([[ 5,  4],
 6        [11, 10],
 7        [11,  7]])
 8  
 9 A@B  == np.dot(A,B)
10 array([[ True,  True],
11        [ True,  True],
12        [ True,  True]])

总结：

 numpy库中可使用运算符 @或dot函数计算。

 

posted @ 2022-08-05 11:12  Tatsukyou  阅读(11185)  评论(1)  编辑  收藏  举报