学习笔记-图灵完备、图灵机与Brainfuck
最近重新研究这个问题，发现之前的错漏太多了，故弃用这一篇，新版将在不久后投稿。
以下是原文
前言
本文是近日对图灵完备的学习所做的笔记,如有错误还请指正.
本文包含以下内容:
1.什么是图灵机?什么是图灵完备?什么是Brianfuck?
2.对图灵机的简单模拟.
3.使用Brianfuck模拟一个简单的图灵机.
图灵机?
Alan Mathison Turing在1937年提出了一个通用计算设备的猜想.他猜想所有的计算都可能在一种特殊的机器上执行,这种机器便是图灵机.
一个图灵机,应该有以下部分.
- 一条无限长度的纸带,它分为相邻的、大小相等的格子,每个格子上能记录至多一个字符,且每个格子都要有一个字符.
- 一个读写头,它能在纸带上左右移动并读写纸带上的字符,并且有一个状态寄存器来记录机器运行的状态.
- 一个指令集,它指明读写头应该做什么.
图灵机的定义
一个图灵机\(M\)可以被定义为一个七元组
其中:
$ Q $ 是一个有限非空的状态集合.
$ \Gamma $ 是一个有限非空的纸带字母表.
$ b \in \Gamma $ 是空白字符,它不属于输入符号集合,在纸带上频繁出现.
$ \Sigma \subseteq \Gamma$ 是输入符号的集合,不包含\(b\).
$ q_0 \in Q $ 是初始状态.
$ F \in Q $ 是接受状态的集合.
\(\delta :(Q\setminus F)\times \Gamma \to Q\times \Gamma \times \{L,R,H\}\)是状态转移函数,它定义了状态转移的规则;(L指读写头左移,R指读写头右移,H指读写头停驻.)
图灵机的运行
- 图灵机从初始状态 \(q_0\) 开始,并且读写头位于纸带的起始位置.
- 根据当前状态和读写头下的符号,图灵机根据状态转移函数 \(\delta\) 执行相应的动作.
- 图灵机继续运行,直到它进入一个接受状态 \(q \in F\) 或者进入一个无法继续执行的状态转移的情况(即无法应用 \(\delta\) 的情况).
- 如果图灵机最终进入\(F\)中的一个状态,则认为输入被接受;否则,如果无法继续执行状态转移,则输入被拒绝.
简单演示
譬如,我们想象下方是一条无限延申的纸带,每一个方格就是一个被分隔出来的格子.我们记空方格□为空字符,把某一些方格涂满■作为另一个字符,读写头为▲,机器的状态为q0.
□□□■□□...
▲
q0
此时,我们只有一个字符■与一个空字符□.
为了操控这台机器,我们还需要一个用来定义\(\delta\)的表,这张表又叫指令集.
由上面的定义我们已经知道,\(\delta\)输入一个两元组,输出一个三元组,即
(□,■)为x,q0,q1,q2为y.只需要在每行中填入(a,b,c)即可完成表格.
| □ | ■ | |
|---|---|---|
| q0 | ... | ... |
| q1 | ... | ... |
| q2 | ... | ... |
由此,只要设计好这个指令集,我们便可以操控上面的机器完成运算.
可计算性
丘奇-图灵论题
若一类问题满足以下条件,则其可被某个图灵机解决,称为图灵可计算的问题.
- 包含有限条清晰的指令.
- 其中的某一个问题可以在有限步内被正确计算.
如果不满足,则该问题是一个图灵不可计算的问题,或者说是目前找不到一个传统的计算模型来解决它.
3 + 4 = ?
接下来,我们来设计一台简单的图灵机,并用它解决一个加法问题3+4.
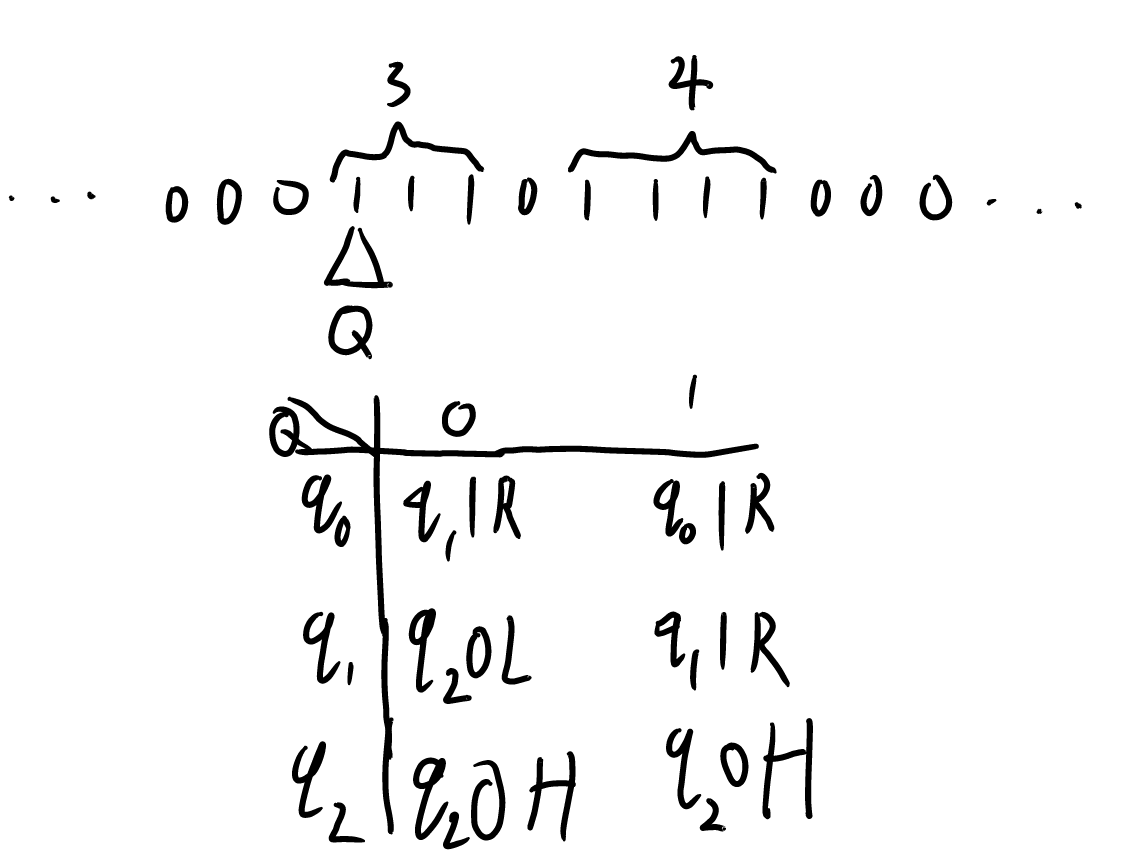
如图所示,
我们记 $0 = b ; 1 \in \Sigma ; q_0,q_1,q_2 \in Q ; $
并用每个字符1的序列的长度来表示数字,如数字3是由三个1组成的序列表示的.
程序开始运行,指针指向第一个1处,状态为\(q_0\),读取数为1.
由表可知此时\(\delta = q_01R\),即读写头右移一位,此时读写头将不断右移直到读取的字符为0.
当读取到0时,\(\delta = q_11R\),即把机器状态改为\(q_1\),把当前格子的字符改为1,并且将读写头右移一位.
此时,机器状态为\(q_1\),机器继续运行.
以此类推,直到程序最后的\(q_20H\),此时读写头什么都不做,机器停机.
不难发现机器事实上是将序列3与序列4中间的0改成了1,然后将序列末尾的一个1改成了0.
于是,我们得到了一个由七个1组成的序列,它表示7,刚刚好是3+4的答案.
由此,我们使用图灵机计算了3+4=7,同时,根据丘奇-图灵论题,我们证明了图灵机有处理加法问题的能力,即加法问题是一个图灵可计算的问题.
图灵完备
现在我们了解了图灵机,图灵完备也就非常简单了.
当一系列操作数据的规则(如编程语言)可以用来模拟图灵机,那么它是图灵完备的.
BrainFuck
简介
BrainFuck是一种极小化的计算机语言，它是由Urban Müller在1993年创建的。
它只有八个有效字符,一个字符就是一条命令,但它是图灵完备的.
| 字符 | 作用 |
|---|---|
| > | 指针向右移动一格 |
| < | 指针向左移动一格 |
| + | 使指针当前格数值加一 |
| - | 使指针当前格数值减一 |
| . | 把当前格数值按 ASCII 表输出到终端 |
| , | 从终端接受一 byte 的数据，存储其 ASCII 数值到当前格 |
| [ | 当指针当前值为 0 时，程序跳转至与之对应的 ] 之后；否则程序正常执行 |
| ] | 程序跳转回与之对应的 [ 处 |
既然BrainFuck是图灵完备的,那么我们就能用它模拟图灵机.
3 + 4 = 7
将BrainFuck工作的数组想象为一条无限长的纸条,上面用空字符0占满了每一个格子.而指向起始位置的指针就是读写头.
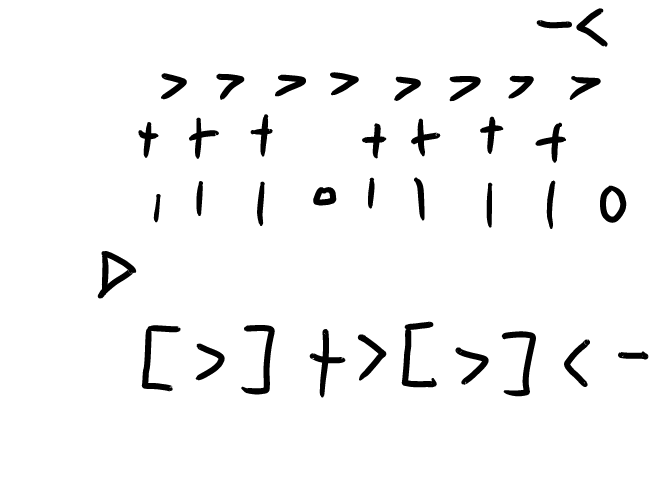
首先我们需要初始化纸带,将序列写上去.
+>+>+>>+>+>+>+<<<<<<<
然后我们按着刚刚实现的简单图灵机的运行,模仿一段代码
[>]+>[>]<-
[>]模仿了图灵机寻找两串字符序列之间的空字符的过程.这与图灵机中的 \(q_0 1 R、q_1 1 R\)作用相同.+>将空字符替换为1并向右移一位.这模拟了图灵机中\(q_1 1 R\)的作用<-回退一位并将其改写为0.这模拟了\(q_2 0 L、q_2 0 H\)的作用.
此时我们发现,只用了八个有效字符中的六个就完成了模拟,那么剩下的,.的作用是什么呢?
从它们的作用描述不难看出,,.是用来写入与读取数据的.
使用这两个符号,能使得数据的读取与写入不再是写死在程序里,而是剥离为交互式的输入输出,这使Brainfuck程序不再是一次性的,而是可以重复使用的.
不难看出,BrainFuck的八个有效字符的组合就可以模拟出图灵机的行动.
<>可以模拟读写头在纸带上的移动+-可以模拟读写头对纸带上数据的擦写.[可以模拟读写头对纸带的读取.[]加上brainfuck代码的顺序实现了对程序状态的把控.模拟了状态寄存器与指令集配合操控程序流程.- brainfuck所操作的数组起了纸带的作用.
,.模拟了对于纸带数据的读取与写入.
综上,我们顺利的使用BrainFuck模拟了图灵机.这也意味着BrainFuck确实是一门图灵完备的语言.
饼
画大饼环节()
事实上,我还是没弄懂,一个严格规范的图灵机应该是怎么样的?
文章中模拟了一个简单的图灵机,但图灵机就长这样吗?是否有其他样式的图灵机呢?如果有的话,图灵机应该是长什么样的?
这导致我心中总有一股不踏实感.但是这部分怕是只能等未来再解决了.总而言之,目前待更新解决的问题如下:
- 什么是接受状态?图灵机进入该状态时会做何行动?
- 图灵机应该是怎么工作的?
- 图灵机在什么情况下才会停机?
修完了(ゝ∀･)
