数据在计算机中的表示 | 进制转换、浮点数表示

计算机中使用的数据可分成两大类：

• 符号数据:非数字符号的表示（ASCII、汉字、图形等）
• 数值数据:数字数据的表示方式（定点、浮点）

文章目录

• 进制转换：
• 10进制整数转任意进制整数（C++代码）
• 任意进制整数转10进制整数（C++代码）
• 浮点数 IEEE 754
• 例1：已知754标准存储格式十六进制，求浮点数十进制数值
• 例2：将十进制浮点数转换为754标准的32位浮点数的二进制存储格式

数据格式：

• 二进制：用0和1两个数码来表示的数。它的基数为2，逢二进一。是计算技术中广泛采用的一种数制。
• 八进制：用3位二进制表示八进制，它的基数为8，逢8进一。
• 十六进制：用4位二进制表示十六进制，它的基数为16，逢16进一。使用 0-9 A-F 分别表示10进制的 0-9 10-15。

二进制	八进制	十六进制	十进制
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	A	10
1011	13	B	11
1100	14	C	12
1101	15	D	13
1110	16	E	14
1111	17	F	15

进制转换：

10进制和R进制之间的转换

• R进制到10进制：
  $\sum_{i=n}^{-m} k_i × r^i$

• 10进制到R进制：
  整数部分：除r取余，r为进制基数
  小数部分：乘r取整

10进制整数转任意进制整数（C++代码）

#include <iostream>
using namespace std;


// 字符串反转
void StrReverse(char* str)
{
	char tmp;
	int len = strlen(str);
	for (int i = 0, j = len - 1; i <= j; i++, j--)
	{
		tmp = str[i];
		str[i] = str[j];
		str[j] = tmp;
	}
	str[len] = '\0';
}

//十进制转任意进制(小于等于36)
void DecToArbitrary(int num, int radix, char* str)
{
	if (radix <= 0)	return;
	str[0] = '0';		// 0 ==》 0
	bool flag = false;	/* 负数 */
	if (num < 0) { num *= -1;	flag = true; }
	
	int i = 0;
	char ch[] = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";
	while (num != 0)
	{
		str[i++] = ch[(num % radix)];
		num /= radix;
	}
	
	if (flag)	str[i] = '-';
	StrReverse(str);
}

int main()
{
	char str[100] = "";

	/* 
		DecToArbitrary(num, r , str);
		将10进制装换为 r 进制
		num(10) ==> str(r)
	*/
	DecToArbitrary(32, 16, str);
	cout << "hex: " str << endl;

	return 0;
}

任意进制整数转10进制整数（C++代码）

#include <iostream>
using namespace std;

// 幂函数
int myPow(int x, int n)
{
	unsigned int z = (n >= 0 ? n : -n);

	for (int tmp = 1; ; x *= x)
	{
		if ((z & 1) != 0)
		{
			tmp *= x;
		}
		if ((z >>= 1) == 0)
		{
			return n >= 0 ? tmp : 1.0 / tmp;
		}
	}
}


//任意进制转十进制(小于等于36)
/* str(r) ==> num(10)   */
void ArbitraryToDec(char* str, int radix, int& num)
{
	num = 0;		// 0 ==》 0
	if (NULL == str || radix < 0 )	return;
	int len = strlen(str);
	int i =  len - 1;
	int sum = 0;
				/* 
					A, B, C, D ...    ascii 65-90 
					a, b, c, d ...    ascii 97-128
				*/
	char ch[] = {10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35};

	while (i >= 0 && isalnum(str[i]))
	{
		int n = 0;
		if (isalpha(str[i]))	// 字母
		{
			int t = 65;
			if (islower(str[i]))	t = 97;
			n = ch[str[i] - 0 - t];

			if (n >= radix)		// error:数位大于进制
			{
				sum = -1;
				break;
			}
		}
		else if (isdigit(str[i]))	// 数字
		{
			n = str[i] - '0';
		}

		sum += n * myPow(radix,len - i -1); 
		i--;
	}

	if (str[0] == '-') sum *= -1;
	num = sum;
}

int main()
{
	int num = 0;
	char str[128] = "";
	
	/*
		ArbitraryToDec(str, r, num);
		将r进制为10装换
		str(r) ==> num(10)
	*/
	cin >> str;
	ArbitraryToDec(str, 16, num);
	cout << "dec: " << num << endl;

	return 0;
}

浮点数 IEEE 754

IEEE754标准(规定了浮点数的表示格式,运算规则等)

• 规则规定了单精度(32)和双精度(64)的基本格式.
• 规则中,尾数用原码,指数用移码(便于对阶和比较)
  
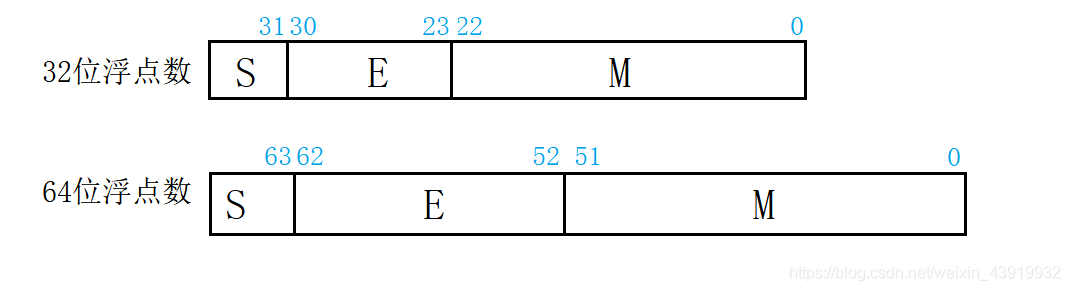
  浮点数的表示：
  
  ——图片来自MOOC

32位的浮点数：

• S数的符号位，1位，在最高位，“0”表示正数，“1”表示负数。
• M是尾数， 23位，在低位部分，采用纯小数表示
• E是阶码，8位，采用移码表示。移码比较大小方便。
• 规格化： 若不对浮点数的表示作出明确规定，同一个浮点数的表示就不是惟一的。
  尾数域最左位(最高有效位)总是1， 故这一位经常不予存储，而认为隐藏在小数点的左边。
  采用这种方式时，将浮点数的指数真值e变成阶码E时，应将指数e加上一个固定的偏移值127(01111111)，即E=e+127

64位的浮点数
符号位1位，阶码域11位，尾数域52位，指数偏移值是1023。因此规格化的64位浮点数x的真值为：
$x=(-1)^S×(1.M)×2^{E-1023}$
e=E-1023
一个规格化的32位浮点数x的真值表示为
$x=(-1)^S×(1.M)×2^{E-127}$
e=E-127

例1：已知754标准存储格式十六进制，求浮点数十进制数值

若浮点数x的754标准存储格式为(41360000)16，求其浮点数的十进制数值。
解：

• 将16进制数展开后，可得二制数格式为
  $0\ \ \ \ \ \ \ 100\ 00010\ \ \ \ \ \ \ \ \ \ 011 0110 0000 0000 0000 0000$
  $S\ \ \ \ \ \ \ 阶码(8位)\ \ \ \ \ \ \ \ \ 尾数(23位)$
• 指数e=阶码-127=10000010-01111111=00000011=(3)10
• 包括隐藏位1的尾数
  1.M=1.011 0110 0000 0000 0000 0000=1.011011
• 于是有
  $x=(-1)S×1.M×2^e=+(1.011011)×2^3=+1011.011=(11.375)_{10}$

C++代码实现

#include <iostream>
#include <bitset>
using namespace std;

void hex_to_float()
{
	// 将16进制转换为2进制
	unsigned long long num = 0x0;
	cin >> hex >> num;
	bitset<32> bit(num);

	// 将2进制准换为float类型
	float res = *(float*)&bit;

	cout << res << endl;		// 输出10进制浮点数形式
	cout << bit << endl;		// 输出IEEE 754 格式二进制
}

int main()
{

	hex_to_float();
	/*
	输入： 0x41360000 或 41360000
	输出：
	11.375
	01000001001101100000000000000000
	*/

	return 0;
}

例2：将十进制浮点数转换为754标准的32位浮点数的二进制存储格式

将数(20.59375)10转换成754标准的32位浮点数的二进制存储格式。
解:

• 首先分别将整数和分数部分转换成二进制数：
  $20.59375=10100.10011$
• 然后移动小数点，使其在第1，2位之间
  $10100.10011=1.010010011×2^4$
  e=4于是得到：S=0, E=4+127=131, M=010010011
• 最后得到32位浮点数的二进制存储格式为：
  01000001101001001100000000000000=(41A4C000)16

C++代码实现

#include <iostream>
#include <bitset>
using namespace std;

void float_to_bin()
{
		float fa;
		cin >> fa;	// 取 fa 地址，强转为 uint64_t 类型地址，解引用为 uint64_t 类型 
		unsigned long long tmp = *(unsigned long long*) & fa;
		bitset<32> bin(tmp);
		cout << bin << endl;
}

void float_to_hex()
{
	float fa;
	cin >> fa;
	unsigned long long tmp = *(unsigned long long*) & fa;
	bitset<32> bin(tmp);

	bitset<32> bit(bin);
	unsigned long a = bit.to_ullong();	// bitset 转 usigned long long
	cout << hex<< a << endl;
}

int main()
{

	float_to_bin();
	/*
	输入：20.59375
	输出：01000001101001001100000000000000
	*/
	float_to_hex();
	/*
	输入：20.59375
	输出：41a4c000
	*/
	return 0;
}

数的机器码表示
真值:一般书写的数
机器码:机器中表示的数, 要解决在计算机内部数的正、负符号和小数点运算问题。

• 原码：符号位加上真值
• 反码：除符号为，其余位皆取反
• 补码：反码+1。
• 移码：对补码符号位取反

注：正数的原码、反码、补码、移码都相同，并且在计算机中存储带有符号的数都是以补码形式存储，用补码形式进行运算的。

如：
[ 1] = [0000 0001]原 = [0000 0001]反 = [0000 0001]补 = [0000 0001]移
[-1] = [1000 0001]原 = [1111 1110]反 = [1111 1111]补 = [0111 1111]移

---

附：
bitset: C ++标准库参考/C ++标准库头文件/bitset Class