高级数据结构 | 树和二叉树

文章目录

• 树的定义：
• 二叉树的概念
• 顺序存储二叉树
• 链式存储二叉树
• 静态结构存储二叉树
• 二叉树遍历 (Binary Tree Traversal)
• 创建二叉树
• 购买结点
• 创建二叉树，输入以‘#’表示空结点
• 传入字符串，创建二叉树（二级指针）

树的定义：

树是由 n (n>= 0)个结点组成的有限集合。如果 n = 0，称为空树；如果 n > 0，则

• 有一个特定的称之为根(root)的结点，它只有直接后继，但没有直接前驱；
• 除根以外的其它结点划分为 m (m >= 0)个互不相交的有限集合 T0, T1, …, Tm-1，每个集合又是一棵树，并且称之为根的子树(subTree)。每棵子树的根结点有且仅有一个直接前驱，但可以有 0 个或多个直接后继。

相关概念：

1. 节点的度：一个节点含有的子树的个数称为该节点的度；
2. 树的度：一棵树中，最大的节点的度称为树的度；
3. 叶节点或终端节点：度为零的节点；
4. 非终端节点或分支节点：度不为零的节点；
5. 父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
6. 孩子节点或子节点：一个节点含有的，子树的根节点，称为该节点的子节点；
7. 兄弟节点：具有相同父节点的节点互称为兄弟节点；
8. 节点的层次：从根开始定义起，根为第 1 层，根的子节点为第 2 层，以此类推；
9. 深度：对于任意节点 n,n 的深度为从根到 n 的唯一路径长，根的深度为 0；
10. 高度：对于任意节点 n,n 的高度为从 n 到一片树叶的最长路径长，所有树叶的高度为 0；
11. 堂兄弟节点：父节点在同一层的节点互为堂兄弟；
12. 节点的祖先：从根到该节点所经分支上的所有节点；
13. 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
14. 森林：由 m（m>=0）棵互不相交的树的集合称为森林；
15. 树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树。反之是有序树

二叉树的概念

二叉树的定义：
一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。

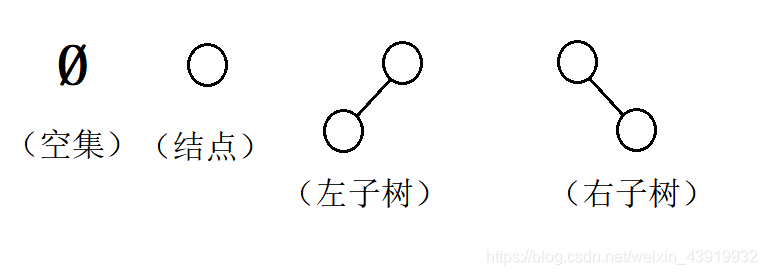
二叉树的性质

• 若二叉树的层次从 0 开始, 则在二叉树的第 i 层最多有 2ⁱ 个结点。(i>= 0) [证明用数学归纳法]
• 高度为 k 的二叉树最多有 2^k+1-1 个结点。(k >= -1) [证明用求等比级数前 k 项和的公式]
• 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为 2 的非叶结点个数为 n2, 则有 n0＝n2＋1。

定义： 满二叉树(Full Binary Tree)： 每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

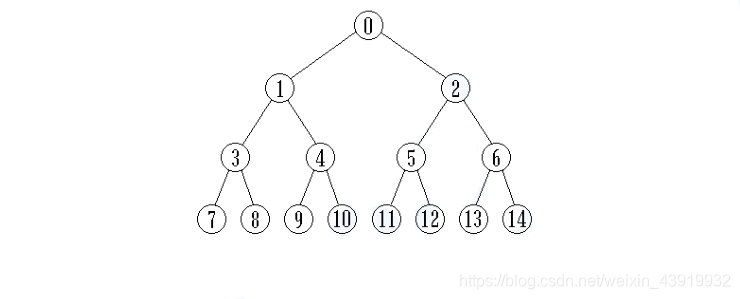
定义： 完全二叉树(Complete Binary Tree)： 若设二叉树的高度为 h，则共有 h+1 层。除第 h 层外，其它各层(0 ~ h-1)的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，这就是完全二叉树。

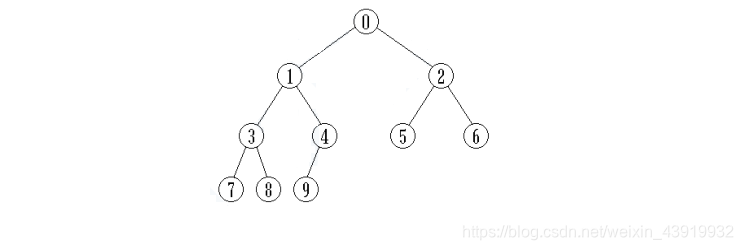
具有n 个结点的完全二叉树的高度为 log₂⁽ⁿ⁺¹⁾ -1 。
证明：
　　设二叉树高度为 h，则 2^h -1 < n ≤ 2^h+1 -1 ⇒ 2^h < n+1 ≤ 2^h+1
　　取对数： h < log₂⁽ⁿ⁺¹⁾ ≤ h+1

二叉树的存储表示；

• 什么数据结构 ： Data_Structure = (D,S)。
• 数据的逻辑结构是对数据之间关系的描述。
• 数据元素之间的关系有两种不同的表示方法：顺序映象和非顺序映象，并由此得到两种不同的存储结构：顺序存储结构和链式存储结构。数据的存储结构是指数据的逻辑结构在计算机中的表示。

顺序存储二叉树

优点：存储密度大，可以方便的表示各元素之间的关系。父节点 = (子节点-1)/2
缺点：只适用与完全二叉树的存放。存放普通二叉树时，会有空间的浪费。比如在有间隔缺省的情况下或极端点的只有左子树或只有右子树等情况，数组中会有很多空间没有被使用，会造成浪费。

链式存储二叉树

typedef char ElemType;
// 二叉链表     
typedef struct BtNode  // BinaryTreeNode   
{   
   struct BtNode *leftchild;   
   struct BtNode *rightchild;   
   ElemType data;   
}BtNode, *BinaryTree;  
//三叉链表
typedef struct BtNode  // BinaryTreeNode   
{   
    struct BtNode *leftchild;   
    struct BtNode *parent;      // 双亲指针 
    struct BtNode *rightchild;   
	ElemType data;   
}BtNode, *BinaryTree;   

其中，三叉链表主要在BST（二叉排序树）、AVL树、红黑树、B树中使用。

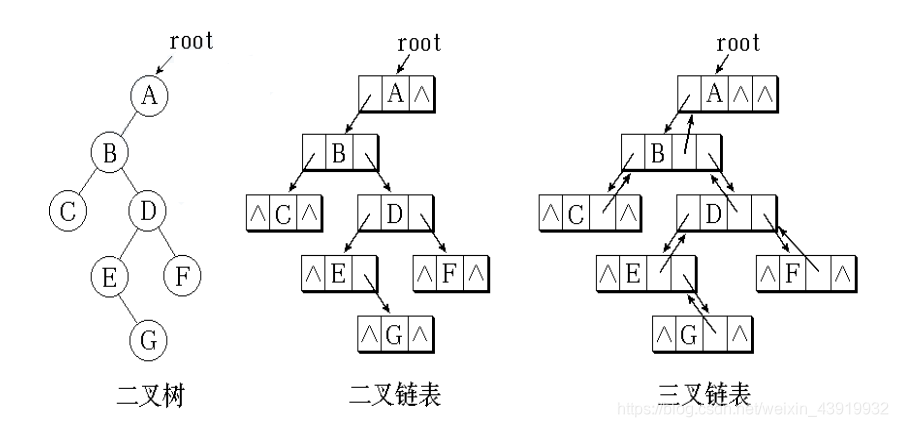
二叉链表缺点：很难通过一个结点找到它的双亲结点。
二叉链表与三叉链表存储对比：
对于一个结点来说是树的最小单元，结点存放的信息越多，编程就越简单，但存放数据的密度就会降低，数据占据结点的空间变少，辅助信息占据空间变多。因此，两者各有特点，我们只需针对不同需求选用合适的结构即可。

静态结构存储二叉树

如：
data:A ，它的双亲结点为 -1，则它是根节点，它的左孩子下标为 1，右孩子下标为 -1.
data:B ，它的双亲结点为 0下标，则A是他的双亲，它的左孩子下标为 2，有孩子下标为 3.
data:C … …
… …

二叉树遍历 (Binary Tree Traversal)

所谓树的遍历，就是按某种次序访问树中的结点，要求每个结点访问一次且仅访问一次。
设访问根结点记作 V；遍历根的左子树记作 L； 遍历根的右子树记作 R；

则可能的遍历次序有：

• 前序　　　VLR　　　镜像　　　VRL

/* 先序遍历 */
void PreOrder(struct BtNode* p)
{
	if (NULL != p)
	{
		printf("%c ", p->data);
		PreOrder(p->leftchild);
		PreOrder(p->rightchild);
	}
}

• 中序　　　LVR　　　镜像　　　RVL

/* 中序遍历 */
void InOrder(struct BtNode* p)
{
	if (NULL != NULL)
	{
		InOrder(p->leftchild);
		printf("%c ", p->data);
		InOrder(p->rightchild);
	}
}

• 后序　　　LRV　　　镜像　　　RLV

/* 后序遍历 */
void PastOrder(struct BtNode* p)
{
	if (NULL != p)
	{
		PastOrder(p->leftchild);
		PastOrder(p->rightchild);
		printf("%c ", p->data);
	}
}

以上三种遍历方式，统称为深度优先遍历。

创建二叉树

购买结点

结点的申请封装成函数，统一结点申请方式。比如对结点申请失败时的处理，或是自己有实现内存池时通过内存池的方式申请结点。增加灵活性。

typedef char ElemType;
typedef struct BtNode
{
	struct BtNode* leftchild;
	struct BtNode* rightchild;
	ElemType data;
}BtNode, * BinaryTree;

/* 购买结点,便于后期维护有关结点的申请的问题 */
struct BtNode* Buynode()
{
	struct BtNode* s = (struct BtNode*)malloc(sizeof(struct BtNode));
	if (NULL == s)	exit(1);
	memset(s, 0, sizeof(struct BtNode));
	return s;
}

void Freenode(struct BtNode *p)
{
	free(p);
}

创建二叉树，输入以‘#’表示空结点

#define	END '#'		// 输入时以‘#’结束

/* 创建二叉树 */
struct BtNode* CreateTree()
{
	struct BtNode* s = NULL;
	ElemType item;
	scanf("%c", &item);
	if (item != END)
	{
		s = Buynode();
		s->data = item;
		s->leftchild = CreateTree();
		s->rightchild = CreateTree();
	}
	return s;
}


int main()
{
	BinaryTree root = NULL;
	root = CreateTree();	// 输入 ABC##DE##F##C#H##
	PreOrder(root); printf("\n");
	InOrder(root);	printf("\n");
	PastOrder(root); printf("\n");
	return 0;
}

传入字符串，创建二叉树（二级指针）

struct BtNode* CreateTree2(const char *str)
{
　　//s->leftchild = CreateTree2(str+1);//error
　　//s->rightchild = CreateTree2(str+1);//error

  //s->leftchild = CreateTree2(++str);//error
　　//s->rightchild = CreateTree2(++str);//error
}

注意：以上两种递归方式都是错误的。要实现以传入字符串的方式创建二叉树就需要用到二级指针。

/* 创建二叉树  ---字符串
	C char**类型 二级指针
*/
struct BtNode* CreateTree1(const char** pstr)
{
	struct BtNode* s = NULL;
	if (NULL != pstr && NULL != *pstr && **pstr != END)
	{
		s = Buynode();
		s->data = **pstr;
		s->leftchild = CreateTree1(& ++ *pstr);
		s->rightchild = CreateTree1(& ++ *pstr);
	}
	return s;
}

/* 创建二叉树  ---字符串
	C++ char*类型的引用
*/
struct BtNode* CreateTree2(const char* &str)
{
	struct BtNode* s = NULL;
	if (NULL != str && *str != END)
	{
		s = Buynode();
		s->data = *str;
		s->leftchild = CreateTree2(++str);
		s->rightchild = CreateTree2(++str);
	}
	return s;
}



int main()
{
	const char* str = "ABC##DE##F##G#H##";
	BinaryTree root = NULL;
	root = CreateTree1(&str);
	//root = CreateTree1(str);
	PreOrder(root); printf("\n");
	InOrder(root);	printf("\n");
	PastOrder(root); printf("\n");
	return 0;
}

最后，如果觉得我的文章对你有帮助的话请帮忙点个赞，你的鼓励就是我学习的动力。如果文章中有错误的地方欢迎指正，有不同意见的同学也欢迎在评论区留言，互相学习。

——学习路上，你我共勉