P1990-覆盖墙壁

分情况:

\[\left\{ \begin{aligned} & 条形 \left\{ \begin{aligned} 横着\\ 竖着\\ \end{aligned}\right. \\ & L形\\ \end{aligned} \right. \]

条形

设 $ F(n)$ 长度为 \(n\) 的方法数

横着

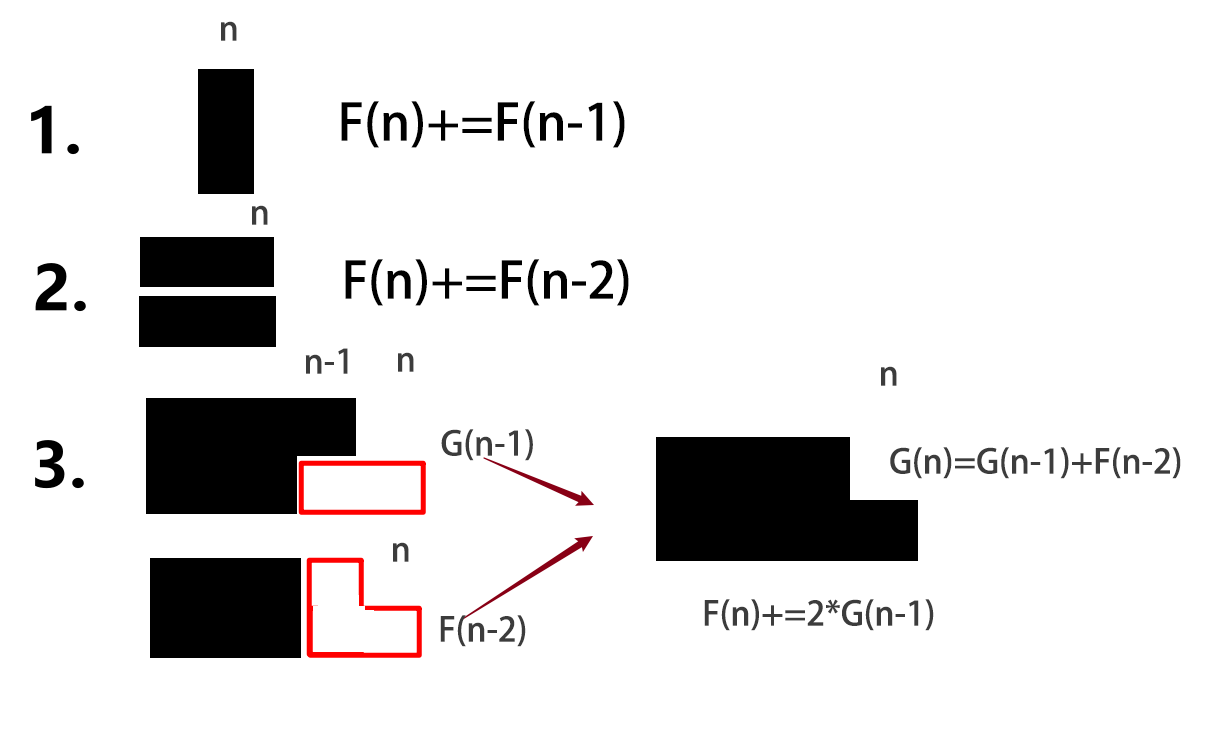
\(F(n)+=F(n-1)\)

竖着

\(F(n)+=F(n-2)\)

L形

设\(G(n)\) 为长度凸出来那一点到 \(n\) 的方法数

\(G(n)=G(n-1)+F(n-2)\)

此为\(G\) 的递推公式

答案

\(F(n)=F(n-1)+F(n-2)+2\times G(n-1)\)

此为\(F\) 的递推公式

初始条件

\[F(0)=1\\ F(1)=1\\ F(2)=2\\\ \\ G(1)=0\\ G(2)=1\\ G(3)=1\\ G(4)=3\\ \]

变式

\[\begin{aligned} &G(n)-G(n-1)=F(n-2)\\ &G(n-1)-G(n-2)=F(n-3)\\ &\cdots\\ &G(4)-G(3)=F(2)\\ &G(3)-G(2)=F(1)\\ &G(2)-G(1)=F(0)\\ &累加得\\ &G(n)=\sum_{k=0}^{n-2} F(k)+G(1)\\ &G(2)=1\\ &G(n)=\sum_{k=0}^{n-2} F(k)\\ \end{aligned} \]

所以\(F(n)\) 得

\[\begin{aligned} &F(n)=F(n-1)+F(n-2)+2\times G(n-1)\\ &带入G(n-1)\\ &得到F(n)=F(i-1)+F(i-2)+2\times\sum_{i=0}^{n-3} F(i)\\ \end{aligned} \]

#include<iostream>
using namespace std;
const int N = 1e7+9;
int F[N];
int main() {
	int n; cin >> n;
	int ch = 0;
	F[0] = 1; F[1] = 1; F[2] = 2;
	for (int i = 3; i <= n; i++) {
		ch += F[i - 3];
		ch %= 10000;
		F[i] = F[i - 1] + F[i - 2] + 2 * ch;
		F[i] %= 10000;
	}
	cout << F[n];
	return 0;
}

或者改为

#include<iostream>
using namespace std;
const int N = 1e7 + 9;
int F[N];
int main() {
	int n; cin >> n;
	int ch = 0;
	F[3] = 1;\\表示n=0的时候
	for (int i = 4; i <= n+3; i++) {
		ch += F[i - 3];
		ch %= 10000;
		F[i] = F[i - 1] + F[i - 2] + 2 * ch;
		F[i] %= 10000;
	}
	cout << F[n+3];
	return 0;
}

由于只用到了\(F(i)\) \(F(i-1)\) \(F(i-2)\) \(F(3)\)

简化为

#include<iostream>
using namespace std;
int main() {
	int n; cin >> n;
	int ch = 0;
	int a = 0, b = 0, c = 1,ans=0;
	for (int i = 1; i <= n; i++) {
		ch += a;
		ch %= 10000;
		ans = b + c + 2 * ch;
		ans %= 10000;
		a = b;
		b = c;
		c = ans;
	}
	cout << ans;
	return 0;
}

\(a\) 表示 \(F[-2]\)

\(b\) 表示 \(F[-1]\)

\(c\) 表示 \(F[0]\)

\(ans\) 表示 \(F[1]\)

分情况:

\[\left\{ \begin{aligned} & 条形 \left\{ \begin{aligned} 横着\\ 竖着\\ \end{aligned}\right. \\ & L形\\ \end{aligned} \right. \]

条形

设 $ F(n)$ 长度为 \(n\) 的方法数

横着

\(F(n)+=F(n-1)\)

竖着

\(F(n)+=F(n-2)\)

L形

设\(G(n)\) 为长度凸出来那一点到 \(n\) 的方法数

\(G(n)=G(n-1)+F(n-2)\)

此为\(G\) 的递推公式

答案

\(F(n)=F(n-1)+F(n-2)+2\times G(n-1)\)

此为\(F\) 的递推公式

初始条件

\[F(0)=1\\ F(1)=1\\ F(2)=2\\\ \\ G(1)=0\\ G(2)=1\\ G(3)=1\\ G(4)=3\\ \]

变式

\[\begin{aligned} &G(n)-G(n-1)=F(n-2)\\ &G(n-1)-G(n-2)=F(n-3)\\ &\cdots\\ &G(4)-G(3)=F(2)\\ &G(3)-G(2)=F(1)\\ &G(2)-G(1)=F(0)\\ &累加得\\ &G(n)=\sum_{k=0}^{n-2} F(k)+G(1)\\ &G(2)=1\\ &G(n)=\sum_{k=0}^{n-2} F(k)\\ \end{aligned} \]

所以\(F(n)\) 得

\[\begin{aligned} &F(n)=F(n-1)+F(n-2)+2\times G(n-1)\\ &带入G(n-1)\\ &得到F(n)=F(i-1)+F(i-2)+2\times\sum_{i=0}^{n-3} F(i)\\ \end{aligned} \]

#include<iostream>
using namespace std;
const int N = 1e7+9;
int F[N];
int main() {
	int n; cin >> n;
	int ch = 0;
	F[0] = 1; F[1] = 1; F[2] = 2;
	for (int i = 3; i <= n; i++) {
		ch += F[i - 3];
		ch %= 10000;
		F[i] = F[i - 1] + F[i - 2] + 2 * ch;
		F[i] %= 10000;
	}
	cout << F[n];
	return 0;
}

或者改为

#include<iostream>
using namespace std;
const int N = 1e7 + 9;
int F[N];
int main() {
	int n; cin >> n;
	int ch = 0;
	F[3] = 1;\\表示n=0的时候
	for (int i = 4; i <= n+3; i++) {
		ch += F[i - 3];
		ch %= 10000;
		F[i] = F[i - 1] + F[i - 2] + 2 * ch;
		F[i] %= 10000;
	}
	cout << F[n+3];
	return 0;
}

由于只用到了\(F(i)\) \(F(i-1)\) \(F(i-2)\) \(F(3)\)

简化为

#include<iostream>
using namespace std;
int main() {
	int n; cin >> n;
	int ch = 0;
	int a = 0, b = 0, c = 1,ans=0;
	for (int i = 1; i <= n; i++) {
		ch += a;
		ch %= 10000;
		ans = b + c + 2 * ch;
		ans %= 10000;
		a = b;
		b = c;
		c = ans;
	}
	cout << ans;
	return 0;
}

\(a\) 表示 \(F[-2]\)

\(b\) 表示 \(F[-1]\)

\(c\) 表示 \(F[0]\)

\(ans\) 表示 \(F[1]\)