20172319 《程序设计与数据结构》 第九周学习总结
20172319 2018.11.09-11.16
《程序设计与数据结构》第9周学习总结
目录
教材学习内容总结
第十五章 图
-
15.1 无向图：
-
图 由结点{顶点（vertice）}和结点之间的链接{边（edge）}构成。
-
无向图（undirected graph） ： 一种边为无序结点对的图。
-
邻接（adjacent） ： 图中的两个顶点之间有一条联通边，则称这两个顶点为邻接的 （邻居（neighbor））。
-
自循环（self-loop）|| 环（sling） ： 联通一个顶点及其自身的边。
-
路径（path） ： 图中的一系列有向边，每条边连通两个顶点。
-
连通的 （connected） ： 有向图中的任意两个顶点之间都存在一条路径。
-
15.2 有向图：
-
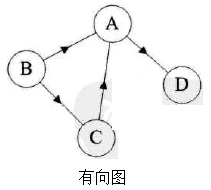
有向图（directed graph）|| 双向图（digraph） ： 一种边为有序结点对的图。
-
邻接（adjacent） ： 图中的两个顶点之间有一条联通边，则称这两个顶点为邻接的 （邻居（neighbor））。
-
自循环（self-loop）|| 环（sling） ： 联通一个顶点及其自身的边。
-
路径（path） ： 图中的一系列边，每条边连通两个顶点。
-
连通的 （connected） ： 无向图中的任意两个顶点之间都存在一条路径。
-
环路（cycle） ： 一种首顶点和末顶点相同且无重边的路径，没有环路的图称为无环的（acyclic） 。
-
无向树（undirected tree） ： 一种连通的无环无向图，其中一个元素被指定为树根。
-
15.3 网络：
-
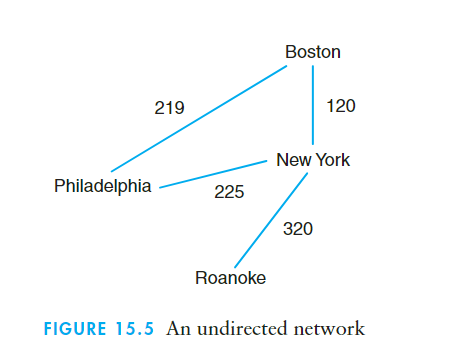
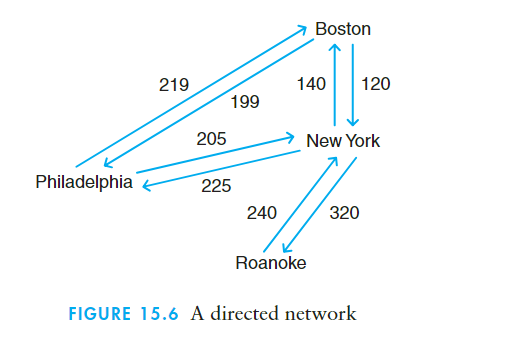
网络（network）|| 加权图（weighted graph） ： 边带有权重的图。
-
15.4 常用的图算法：
-
15.4.1 遍历：
-
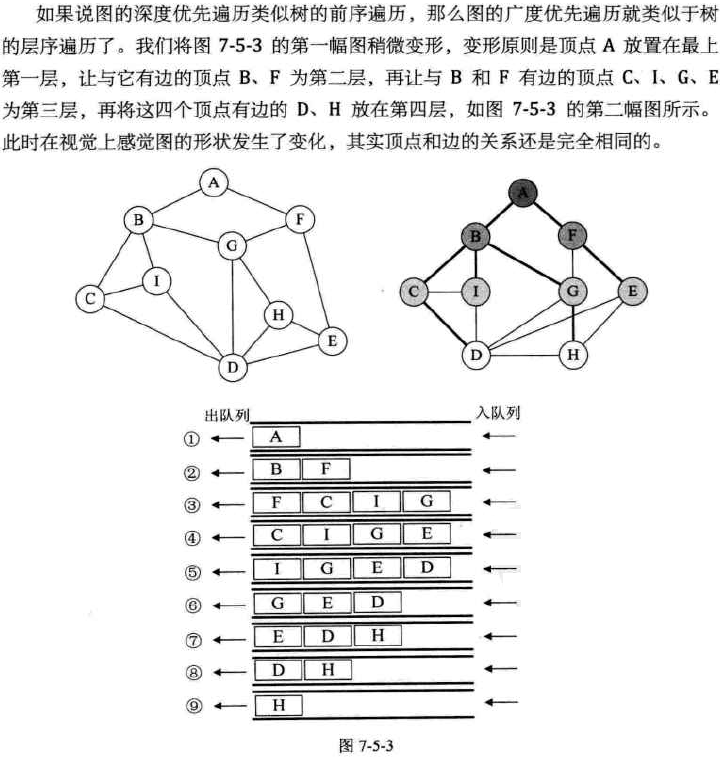
广度优先遍历（breadth-first traversal） : 类似于树的层次遍历。
-
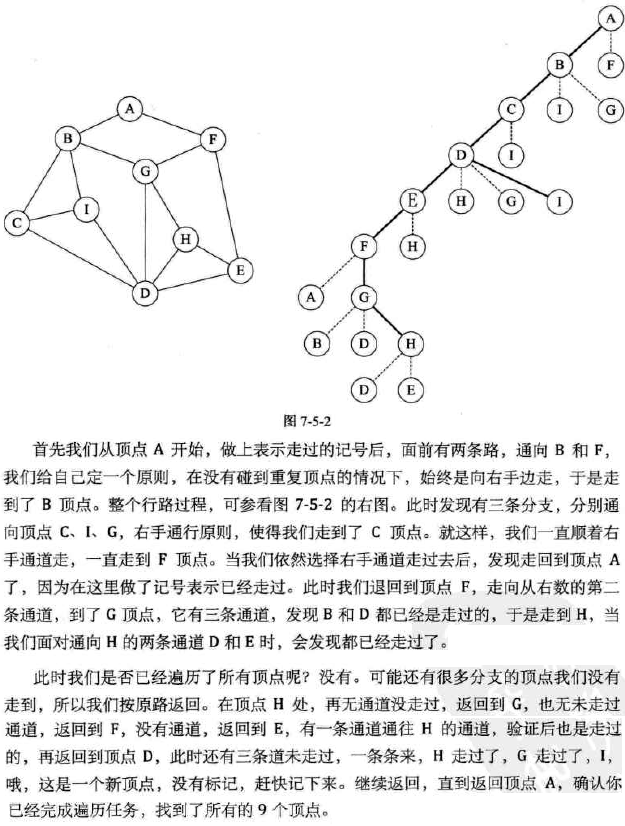
深度优先遍历（depth-first traversal） ： 类似于树的前序遍历。
-
15.4.2 测试连通性：
-
选择任意顶点为起始点，当且仅当广度优先遍历中的顶点数目等于图中的顶点个数时，该图连通。
-
15.4.3 最小生成树：
-
生成树（spanning tree） ： 一棵含有图中所有顶点和部分边的树。
-
最小生成树（minimun spanning tree，MST） ： 其边的权重总和小于或等于同一个图中其他任何一棵生成树的权重总和。
-
性质：
-
最小生成树不能有回路。
-
最小生成树可能是一个，也可能是多个。
-
最小生成树边的个数等于顶点的个数减一。
-
15.4.4 判定最短路径：
-
1.寻找两个顶点之间的最小边数。
-
2.寻找加权图的最便宜路径。
-
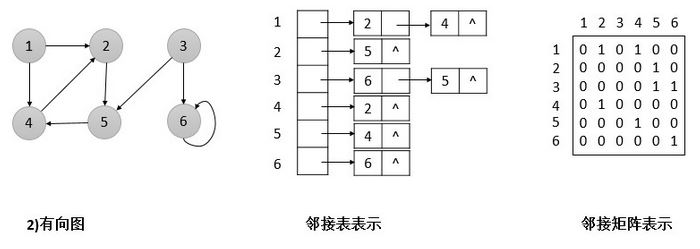
15.5 图的实现策略：
通常采用邻接表表示法，因为以此来表示稀疏图（图中边数远小于点个数） 比较紧凑。但当遇到稠密图通常采用邻接矩阵表示法，例如求最短路径算法中，就采用邻接矩阵表示。
教材学习中的问题和解决过程
- 问题1：
- 解决：
代码调试中的问题和解决过程
-
问题1：
-
解决：
代码托管
上周考试错题总结
- 错题1：上周无测试。
- 解决：
- 错题2：
- 解决：
- 错题3：
- 解决：
结对及互评
点评过的同学博客和代码
- 本周结对学习情况：
- 20172316赵乾宸
- 博客中值得学习的或存在问题：
- 20172329王文彬
- **博客中值得学习的或存在问题： **
- 博客内容充实、排版整齐、对教材内容有经过一番认真思考、继续保持。
- 代码截图做标注时应尽量避免遮挡代码。
- Markdown的部分缩进有误。
- 教材问题2提出得很好，可以看出近断时间来反复使用链表、数组去实现同一类型的数据结构起得了一定的成效。
学习进度条
| 代码行数（新增/累积） | 博客量（新增/累积） | 学习时间（新增/累积） | |
|---|---|---|---|
| 目标 | 3000行 | 15篇 | 300小时 |
| 第一周 | 0/0 | 1/1 | 12/12 |
| 第二周 | 935/935 | 1/2 | 24/36 |
| 第三周 | 849/1784 | 1/3 | 34/70 |
| 第四周 | 3600/5384 | 1/5 | 50/120 |
| 第五周 | 2254/7638 | 1/7 | 50/170 |
| 第六周 | 2809/10447 | 1/9 | 45/215 |
| 第七周 | 3700/14147 | 1/10 | 40/255 |
| 第八周 | 3422/17569 | 1/11 | 36/291 |
| 第九周 | 3862/21431 | 1/12 | 40/331 |
