20172319 实验二《树》实验报告
20172319 2018.11.04-11.12
实验二《树》 实验报告
课程名称:《程序设计与数据结构》
学生班级:1723班
学生姓名:唐才铭
学生学号:20172319
实验教师:王志强老师
课程助教:张师瑜学姐、张之睿学长
实验时间:2018年11月04日——2018年11月12日
必修/选修:必修
目录
实验内容
- 实验二-1-实现二叉树: 完成链树LinkedBinaryTree的实现。
- 实验二 树-2-中序先序序列构造二叉树: 基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能
- 实验二 树-3-决策树: 自己设计并实现一颗决策树
- 实验二 树-4-表达式树: 输入中缀表达式,使用树将中缀表达式转换为后缀表达式,并输出后缀表达式和计算结果
- 实验二 树-5-二叉查找树: 完成PP11.3
- 实验二 树-6-红黑树分析: 参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树(TreeMap,HashMap)进行源码分析,并在实验报告中体现分析结果
实验要求
- 完成蓝墨云上与实验二《树》相关的活动,及时提交代码运行截图和码云Git链接,截图要有学号水印,否则会扣分。
- 完成实验、撰写实验报告,实验报告以博客方式发表在博客园,注意实验报告重点是运行结果,遇到的问题(工具查找,安装,使用,程序的编辑,调试,运行等)、解决办法(空洞的方法如“查网络”、“问同学”、“看书”等一律得0分)以及分析(从中可以得到什么启示,有什么收获,教训等)。报告可以参考范飞龙老师的指导。
- 严禁抄袭,有该行为者实验成绩归零,并附加其他惩罚措施。
实验步骤
- 实验二-1-实现二叉树:
参考教材p212,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台 - 实验二 树-2-中序先序序列构造二叉树:
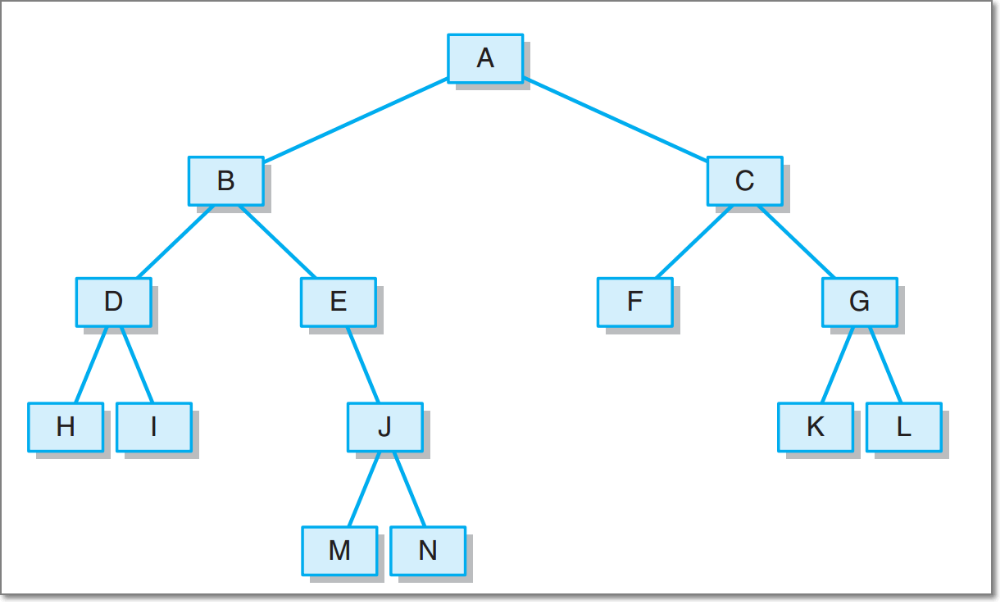
基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
![]()
- 实验二 树-3-决策树:
自己设计并实现一颗决策树
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台 - 实验二 树-4-表达式树:
输入中缀表达式,使用树将中缀表达式转换为后缀表达式,并输出后缀表达式和计算结果(如果没有用树,则为0分)
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台 - 实验二 树-5-二叉查找树:
完成PP11.3
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台 - 实验二 树-5-二叉查找树:
参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树(TreeMap,HashMap)进行源码分析,并在实验报告中体现分析结果。
(C:\Program Files\Java\jdk-11.0.1\lib\src\java.base\java\util)
前期准备:
- 预先下载安装好IDEA 。
需求分析:
- 需要掌握二叉查找树的相关知识;
- 需要掌握当任意给出两个序能构建出唯一一棵二叉树;
- 需要理解表达式树的实现;
- 需要理解决策树的实现。
代码实现及解释
本次实验一共分为六个提交点:
- 实验二-1-实现二叉树:
- 要实现的方法有:
getRight;contains;toString;preorder;postorder; getRight是获取右子树,但这里并没有准确说明针对哪种结点的操作,为了程序的完整性,便实现了可调用如何结点的右子树。getRight具体代码如下:
// 获取某一结点的右子树
public String getNodeRightTree(T Elemnet){
String result;
BinaryTreeNode node = new BinaryTreeNode(Elemnet);
LinkedBinaryTree linkedBinaryTree = new LinkedBinaryTree();
linkedBinaryTree.root = root;
if (root==null){
return "";
}
else {
if (root != null && root.left == null && root.right == null) {
linkedBinaryTree.root = root;
result = linkedBinaryTree.printTree();
return result;
}
node = findNode(Elemnet,root);
if (node.right!=null){
linkedBinaryTree.root = node.right;
result = linkedBinaryTree.printTree();
}
else {
result = "该结点无右子树";
}
return result;
}
}
-
实现结果截图:
![]()
-
contains判断树中是否包含某一元素,这里使用了原有的find方法,使得实现更加便捷。 -
contains具体代码如下:
@Override
public boolean contains(T targetElement)
{
// To be completed as a Programming seatwork
T temp;
boolean found = false;
try {
temp = find(targetElement);
found = true;
}
catch (Exception ElementNotFoundExecption){
found = false;
}
return found;
}
find的具体代码如下:
@Override
public T find(T targetElement) throws ElementNotFoundException
{
BinaryTreeNode<T> current = findNode(targetElement, root);
if (current == null) {
throw new ElementNotFoundException("LinkedBinaryTree");
}
return (current.getElement());
}
-
实现结果截图:
![]()
-
toString是输出树中元素,原本是直接通过一个遍历算法来输出,但为了实验的直观和便于操作,借用了表达式中的printTree -
toString具体代码:此处用了前序遍历来输出
@Override
public String toString()
{
// To be completed as a Programming seatwork
ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
preOrder(root,tempList);
return tempList.toString();
}
printTree具体代码:
public String printTree()
{
UnorderedListADT<BinaryTreeNode<T>> nodes =
new ArrayUnorderedList<BinaryTreeNode<T>>();
UnorderedListADT<Integer> levelList =
new ArrayUnorderedList<Integer>();
BinaryTreeNode<T> current;
String result = "";
int printDepth = this.getHeight();
int possibleNodes = (int)Math.pow(2, printDepth + 1);
int countNodes = 0;
nodes.addToRear(root);
Integer currentLevel = 0;
Integer previousLevel = -1;
levelList.addToRear(currentLevel);
while (countNodes < possibleNodes)
{
countNodes = countNodes + 1;
current = nodes.removeFirst();
currentLevel = levelList.removeFirst();
if (currentLevel > previousLevel)
{
result = result + "\n\n";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++) {
result = result + " ";
}
}
else
{
for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)
{
result = result + " ";
}
}
if (current != null)
{
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
}
else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
return result;
}
-
实现结果截图:
![]()
-
preorder,postorder,书上只给了inorder的实现,只需更改遍历结点的顺序即可实现: -
preorder与postorder具体代码如下:
private void preOrder(BinaryTreeNode<T> node,
ArrayUnorderedList<T> tempList)
{
// To be completed as a Programming seatwork
if (node!=null){
tempList.addToRear(node.element);
preOrder(node.left,tempList);
preOrder(node.right,tempList);
}
}
private void postOrder(BinaryTreeNode<T> node,
ArrayUnorderedList<T> tempList)
{
// To be completed as a Programming seatwork
if (node != null)
{
postOrder(node.getLeft(), tempList);
postOrder(node.getRight(), tempList);
tempList.addToRear(node.getElement());
}
}
-
实现结果截图:
![]()
-
实验二 树-2-中序先序序列构造二叉树:
-
先整明白如何通过给定的两个不同遍历来构建一棵唯一的二叉树,在一轮递归中用两个指针分别指向前序和中序中的元素,遍历前序和中序,当两个指针指向的元素一样时,结束该轮次,记录下一次遍历前序的起始位置,开始下轮遍历。
-
具体代码如下:
// 前序中序构建二叉树
public BinaryTreeNode BuildTree(char[] preorder, char[] inorder) {
return BuildLinkedBinaryTree(preorder, inorder, 0, inorder.length - 1, inorder.length);
}
/**
* @param preorder 前序
* @param inorder 中序
* @param Start 起始位置
* @param End 终止位置
* @param length 结点个数
*/
public BinaryTreeNode BuildLinkedBinaryTree(char[] preorder,char[] inorder,int Start, int End,int length) {
if (preorder==null||preorder.length == 0 || inorder == null
|| inorder.length == 0 || length <= 0){
return null;
}
BinaryTreeNode binaryTreeNode;
binaryTreeNode = new BinaryTreeNode(preorder[Start]);
if (length==1){
return binaryTreeNode;
}
int flag=0;
while (flag < length){
if (preorder[Start] == inorder[End - flag]){
break;
}
flag++;
}
binaryTreeNode.left = BuildLinkedBinaryTree(preorder, inorder,Start + 1, End - flag - 1, length - 1 - flag);
binaryTreeNode.right = BuildLinkedBinaryTree(preorder, inorder,Start + length - flag, End, flag );
return binaryTreeNode;
}
-
实现结果截图:
![]()
-
实验二 树-3-决策树:
-
自己想好所决策需要的问题,修改先前文件的内容即可:
-
实现结果截图:
![]()
-
实验二 树-4-表达式树
-
实现思想:
-
数字是叶子节点,操作符为根节点。
-
先用中缀表达式构建成树,之后后序遍历可得其后缀表达式;
-
构树过程:
-
从表达式的最后一位元素往前扫描,当遇到最后计算的运算符(+或-)时,作为当前根节点,运算符左侧表达式作为左节点,右侧表达式作为右节点,然后递归处理。
-
具体代码如下:
private boolean priority(String[] operator,int size){
// 先对有+ - 的式子进行拆分
boolean found1 = true,found2=true ,found = true;
for (int i = 0 ; i< size;i++) {
if (operator[i].equals("+")) {
found1 = false;
}
}
for (int i = 0 ; i< size;i++) {
if (operator[i].equals("-")) {
found2 = false;
}
}
if (found1 == false||found2==false){
found = false;
}
return found;
}
public BinaryTreeNode Build_Expression_Tree(String[] expression, int size){
// 带括号的式子暂未实现(递归出现的问题太多了(╬ ̄皿 ̄))
BinaryTreeNode binaryTreeNode = new BinaryTreeNode(null);
int length = size; // 元素个数
String[] expression_Left_Tree = null; // 左子树
String[] expression_Right_Tree = null; // 右子树
for (int i = length - 1; i > 0; i--){ // 遍历数组元素
String temp = expression[i];
if (temp.equals("+") || temp.equals("-")) { // 若遇到+ - ,则对数组进行此元素左右分割
binaryTreeNode = new BinaryTreeNode(temp);
expression_Left_Tree = new String[i];
expression_Right_Tree = new String[length - i - 1];
for (int j = 0; j < expression_Left_Tree.length; j++) { // 拆分结点左边数组(左子树)
expression_Left_Tree[j] = expression[j];
}
for (int k = 0; k < expression_Right_Tree.length; k++) {// 拆分结点右边数组(右子树)
expression_Right_Tree[k] = expression[i + k + 1];
}
if (expression_Left_Tree.length == 1) { // 若结点左子树数组长度为1
binaryTreeNode.setLeft(new BinaryTreeNode(expression_Left_Tree[0]));// 输出数组元素并建立左孩子
if (expression_Right_Tree.length!=1){ // 对该结点右端进行建树,后面情况大致一样不做多余复述
binaryTreeNode.setRight(Build_Expression_Tree(expression_Right_Tree,expression_Right_Tree.length));
}
if (expression_Right_Tree.length==1){
binaryTreeNode.setRight(new BinaryTreeNode(expression_Right_Tree[0]));
}
return binaryTreeNode;
}
if (expression_Right_Tree.length == 1) {
binaryTreeNode.setRight(new BinaryTreeNode(expression_Right_Tree[0]));
if (expression_Left_Tree.length!=1){
binaryTreeNode.setLeft(Build_Expression_Tree(expression_Left_Tree,expression_Left_Tree.length));
}
if (expression_Left_Tree.length==1){
binaryTreeNode.setLeft(new BinaryTreeNode(expression_Left_Tree[0]));
}
return binaryTreeNode;
}
break;
}
else if (priority(expression,expression.length)!=false){ // 优先级判断,此刻数组里已无加减号
if (temp.equals("*") || temp.equals("/")) { // 若遇到+ - ,则对数组进行此元素左右分割
binaryTreeNode = new BinaryTreeNode(temp);
expression_Left_Tree = new String[i];
expression_Right_Tree = new String[length - i - 1];
for (int j = 0; j < expression_Left_Tree.length; j++) {
expression_Left_Tree[j] = expression[j];
}
for (int k = 0; k < expression_Right_Tree.length; k++) {
expression_Right_Tree[k] = expression[i + k + 1];
}
if (expression_Left_Tree.length == 1) {
binaryTreeNode.setLeft(new BinaryTreeNode(expression_Left_Tree[0]));
if (expression_Right_Tree.length!=1){
binaryTreeNode.setRight(Build_Expression_Tree(expression_Right_Tree,expression_Right_Tree.length));
}
if (expression_Right_Tree.length==1){
binaryTreeNode.setRight(new BinaryTreeNode(expression_Right_Tree[0]));
}
return binaryTreeNode;
}
if (expression_Right_Tree.length == 1) {
binaryTreeNode.setRight(new BinaryTreeNode(expression_Right_Tree[0]));
if (expression_Left_Tree.length!=1){
binaryTreeNode.setLeft(Build_Expression_Tree(expression_Left_Tree,expression_Left_Tree.length));
}
if (expression_Left_Tree.length==1){
binaryTreeNode.setLeft(new BinaryTreeNode(expression_Left_Tree[0]));
}
return binaryTreeNode;
}
break;
}
}
}
binaryTreeNode.setLeft(Build_Expression_Tree(expression_Left_Tree,expression_Left_Tree.length));
binaryTreeNode.setRight(Build_Expression_Tree(expression_Right_Tree,expression_Right_Tree.length));
return binaryTreeNode;
}
- 运行结果截图:

- 实验二 树-5-二叉查找树
- 完成PP11.3:实现
removeMin;findMin;findMax操作: - 具体代码如下:
@Override
public T removeMin() throws EmptyCollectionException
{
T result = null;
if (isEmpty()) {
throw new EmptyCollectionException("LinkedBinarySearchTree");
} else
{
if (root.left == null)
{
result = root.element;
root = root.right;
}
else
{
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.left;
while (current.left != null)
{
parent = current;
current = current.left;
}
result = current.element;
parent.left = current.right;
}
modCount--;
}
return result;
}
@Override
public T findMin() throws EmptyCollectionException
{
// To be completed as a Programming Project
T result = null;
if (isEmpty()) {
throw new EmptyCollectionException("LinkedBinarySearchTree");
} else
{
if (root.left == null)
{
result = root.element;
root = root.right;
}
else
{
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.left;
while (current.left != null)
{
parent = current;
current = current.left;
}
result = current.element;
parent.left = current;
}
}
return result;
}
@Override
public T findMax() throws EmptyCollectionException
{
// To be completed as a Programming Project
T result = null;
if (isEmpty()) {
throw new EmptyCollectionException("LinkedBinarySearchTree");
} else
{
if (root.right== null)
{
result = root.element;
root = root.left;
}
else
{
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.right;
while (current.right != null)
{
parent = current;
current = current.right;
}
result = current.element;
parent.right = current;
}
}
return result;
}
-
实现结果截图:
![]()
-
实验二 树-6-红黑树分析
-
TreeMap: -
TreeMap 是一个有序的key-value集合,它是通过红黑树实现的。
TreeMap 继承于AbstractMap,所以它是一个Map,即一个key-value集合。
TreeMap 实现了NavigableMap接口,意味着它支持一系列的导航方法。比如返回有序的key集合。
TreeMap 实现了Cloneable接口,意味着它能被克隆。
TreeMap 实现了java.io.Serializable接口,意味着它支持序列化。
TreeMap基于红黑树(Red-Black tree)实现。该映射根据其键的自然顺序进行排序,或者根据创建映射时提供的 Comparator 进行排序,具体取决于使用的构造方法。
TreeMap的基本操作 containsKey、get、put 和 remove 的时间复杂度是 log(n) 。
另外,TreeMap是非同步的。 它的iterator 方法返回的迭代器是fail-fastl的。 -
1.类名及成员:
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable
{
// 比较器对象
private final Comparator<? super K> comparator;
// 根节点
private transient Entry<K,V> root;
// 集合大小
private transient int size = 0;
// 树结构被修改的次数
private transient int modCount = 0;
// 静态内部类用来表示节点类型
static final class Entry<K,V> implements Map.Entry<K,V> {
K key; // 键
V value; // 值
Entry<K,V> left; // 指向左子树的引用(指针)
Entry<K,V> right; // 指向右子树的引用(指针)
Entry<K,V> parent; // 指向父节点的引用(指针)
boolean color = BLACK; //
}
}
- 2.类构造方法:
public TreeMap() { // 1,无参构造方法
comparator = null; // 默认比较机制
}
public TreeMap(Comparator<? super K> comparator) { // 2,自定义比较器的构造方法
this.comparator = comparator;
}
public TreeMap(Map<? extends K, ? extends V> m) { // 3,构造已知Map对象为TreeMap
comparator = null; // 默认比较机制
putAll(m);
}
public TreeMap(SortedMap<K, ? extends V> m) { // 4,构造已知的SortedMap对象为TreeMap
comparator = m.comparator(); // 使用已知对象的构造器
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
- 3.红黑树:
- (1) 结点颜色及其对应类:
// 红黑树的节点颜色--红色
private static final boolean RED = false;
// 红黑树的节点颜色--黑色
private static final boolean BLACK = true;
// “红黑树的节点”对应的类。
// 包含了 key(键)、value(值)、left(左孩子)、right(右孩子)、parent(父节点)、color(颜色)
static final class Entry<K,V> implements Map.Entry<K,V> {
// 键
K key;
// 值
V value;
// 左孩子
Entry<K,V> left = null;
// 右孩子
Entry<K,V> right = null;
// 父节点
Entry<K,V> parent;
// 当前节点颜色
boolean color = BLACK;
// 构造函数
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
// 返回“键”
public K getKey() {
return key;
}
// 返回“值”
public V getValue() {
return value;
}
// 更新“值”,返回旧的值
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
// 判断两个节点是否相等的函数,覆盖equals()函数。
// 若两个节点的“key相等”并且“value相等”,则两个节点相等
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
// 覆盖hashCode函数。
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
// 覆盖toString()函数。
public String toString() {
return key + "=" + value;
}
}
- (2) 在树中结点的共同操作:
// 返回“红黑树的第一个节点”
final Entry<K,V> getFirstEntry() {
Entry<K,V> p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}
// 返回“红黑树的最后一个节点”
final Entry<K,V> getLastEntry() {
Entry<K,V> p = root;
if (p != null)
while (p.right != null)
p = p.right;
return p;
}
// 返回“节点t的后继节点”
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
// 返回“节点t的前继节点”
static <K,V> Entry<K,V> predecessor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.left != null) {
Entry<K,V> p = t.left;
while (p.right != null)
p = p.right;
return p;
} else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.left) {
ch = p;
p = p.parent;
}
return p;
}
}
// 返回“节点p的颜色”
// 根据“红黑树的特性”可知:空节点颜色是黑色。
private static <K,V> boolean colorOf(Entry<K,V> p) {
return (p == null ? BLACK : p.color);
}
// 返回“节点p的父节点”
private static <K,V> Entry<K,V> parentOf(Entry<K,V> p) {
return (p == null ? null: p.parent);
}
// 设置“节点p的颜色为c”
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}
// 设置“节点p的左孩子”
private static <K,V> Entry<K,V> leftOf(Entry<K,V> p) {
return (p == null) ? null: p.left;
}
// 设置“节点p的右孩子”
private static <K,V> Entry<K,V> rightOf(Entry<K,V> p) {
return (p == null) ? null: p.right;
}
- (3)结点的旋转:
// 对节点p执行“左旋”操作
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
// 对节点p执行“右旋”操作
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
- (4)结点的插入和删除
// 插入之后的修正操作。
// 目的是保证:红黑树插入节点之后,仍然是一颗红黑树
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
// 删除“红黑树的节点p”
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry<K,V> s = successor (p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
// 删除之后的修正操作。
// 目的是保证:红黑树删除节点之后,仍然是一颗红黑树
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}

-
红黑树的性质:
-
1、节点是红色或黑色
2、根节点是黑色
3、所有的叶子(NIL空节点)是黑色的
4、每个红色节点的两个儿子均为黑色,即不可能有连续的两个红色节点
5、从任一节点到其叶子(NIL空节点)的路径都包含相同数目的黑节点 -
put方法
// 将“key, value”添加到TreeMap中
// 理解TreeMap的前提是掌握“红黑树”。
// 若理解“红黑树中添加节点”的算法,则很容易理解put。
public V put(K key, V value) {
Entry<K,V> t = root;
// 若红黑树为空,则插入根节点
if (t == null) {
// TBD:
// 5045147: (coll) Adding null to an empty TreeSet should
// throw NullPointerException
//
// compare(key, key); // type check
root = new Entry<K,V>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
// 在二叉树(红黑树是特殊的二叉树)中,找到(key, value)的插入位置。
// 红黑树是以key来进行排序的,所以这里以key来进行查找。
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 新建红黑树的节点(e)
Entry<K,V> e = new Entry<K,V>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 红黑树插入节点后,不再是一颗红黑树;
// 这里通过fixAfterInsertion的处理,来恢复红黑树的特性。
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
-
代码分析
-
1.校验根节点:校验根节点是否为空,若为空则根据传入的key-value的值创建一个新的节点,若根节点不为空则继续第二步
2.寻找插入位置:由于TreeMap内部是红黑树实现的,在插入元素时,遍历左子树,或者右子树
3.新建并恢复:在第二步中实际上是需要确定当前插入节点的位置,而这一步是实际的插入操作,而插入之后为啥还需要调用fixAfterInsertion方法,红黑树插入一个节点后可能会破坏红黑树的性质,因此需要使红黑树从新达到平衡, -
HashMap: -
TreeNode: HashMap的静态内部类,继承与LinkedHashMap.Entry<K,V>类,真正维护红黑树结构的方法都在其内部。
static final class TreeNode<K, V> extends LinkedHashMap.Entry<K, V>
{
TreeNode<K, V> parent; // red-black tree links
TreeNode<K, V> left;
TreeNode<K, V> right;
TreeNode<K, V> prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node<K, V> next)
{
super(hash, key, val, next);
}
final void treeify(Node<K,V>[] tab)
{
// ......
}
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x)
{
// ......
}
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root, TreeNode<K,V> p)
{
// ......
}
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root, TreeNode<K,V> p)
{
// ......
}
// ......其余方法省略
}
treeifyBin:在HashMap中put方法时候,但数组中某个位置的链表长度大于某一值时,会调用treeifyBin方法将链表转化为红黑树。
final void treeifyBin(Node<K, V>[] tab, int hash)
{
int n, index;
Node<K, V> e;
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
// resize()方法这里不过多介绍,感兴趣的可以去看上面的链接。
resize();
// 通过hash求出bucket的位置。
else if ((e = tab[index = (n - 1) & hash]) != null)
{
TreeNode<K, V> hd = null, tl = null;
do
{
// 将每个节点包装成TreeNode。
TreeNode<K, V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else
{
// 将所有TreeNode连接在一起此时只是链表结构。
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
// 对TreeNode链表进行树化。
hd.treeify(tab);
}
}
treeify:将Treenode链转化成红黑树,第一次循环会将链表中的首节点作为红黑树的根,而后的循环会将链表中的的项通过比较hash值然后连接到相应树节点的左边或者右边,插入可能会破坏树的结构。
final void treeify(Node<K, V>[] tab)
{
TreeNode<K, V> root = null;
// 以for循环的方式遍历刚才我们创建的链表。
for (TreeNode<K, V> x = this, next; x != null; x = next)
{
// next向前推进。
next = (TreeNode<K, V>) x.next;
x.left = x.right = null;
// 为树根节点赋值。
if (root == null)
{
x.parent = null;
x.red = false;
root = x;
} else
{
// x即为当前访问链表中的项。
K k = x.key;
int h = x.hash;
Class<?> kc = null;
// 此时红黑树已经有了根节点,上面获取了当前加入红黑树的项的key和hash值进入核心循环。
// 这里从root开始,是以一个自顶向下的方式遍历添加。
// for循环没有控制条件,由代码内break跳出循环。
for (TreeNode<K, V> p = root;;)
{
// dir:directory,比较添加项与当前树中访问节点的hash值判断加入项的路径,-1为左子树,+1为右子树。
// ph:parent hash。
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null && (kc = comparableClassFor(k)) == null)
|| (dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
// xp:x parent。
TreeNode<K, V> xp = p;
// 找到符合x添加条件的节点。
if ((p = (dir <= 0) ? p.left : p.right) == null)
{
x.parent = xp;
// 如果xp的hash值大于x的hash值,将x添加在xp的左边。
if (dir <= 0)
xp.left = x;
// 反之添加在xp的右边。
else
xp.right = x;
// 维护添加后红黑树的红黑结构。
root = balanceInsertion(root, x);
// 跳出循环当前链表中的项成功的添加到了红黑树中。
break;
}
}
}
}
// Ensures that the given root is the first node of its bin,自己翻译一下。
moveRootToFront(tab, root);
}
balanceInsertion: 重新平衡二叉树
static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x)
{
// 正如开头所说,新加入树节点默认都是红色的,不会破坏树的结构。
x.red = true;
// 这些变量名不是作者随便定义的都是有意义的。
// xp:x parent,代表x的父节点。
// xpp:x parent parent,代表x的祖父节点
// xppl:x parent parent left,代表x的祖父的左节点。
// xppr:x parent parent right,代表x的祖父的右节点。
for (TreeNode<K, V> xp, xpp, xppl, xppr;;)
{
// 如果x的父节点为null说明只有一个节点,该节点为根节点,根节点为黑色,red = false。
if ((xp = x.parent) == null)
{
x.red = false;
return x;
}
// 进入else说明不是根节点。
// 如果父节点是黑色,那么大吉大利(今晚吃鸡),红色的x节点可以直接添加到黑色节点后面,返回根就行了不需要任何多余的操作。
// 如果父节点是红色的,但祖父节点为空的话也可以直接返回根此时父节点就是根节点,因为根必须是黑色的,添加在后面没有任何问题。
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 一旦我们进入到这里就说明了两件是情
// 1.x的父节点xp是红色的,这样就遇到两个红色节点相连的问题,所以必须经过旋转变换。
// 2.x的祖父节点xpp不为空。
// 判断如果父节点是否是祖父节点的左节点
if (xp == (xppl = xpp.left))
{
// 父节点xp是祖父的左节点xppr
// 判断祖父节点的右节点不为空并且是否是红色的
// 此时xpp的左右节点都是红的,所以直接进行上面所说的第三种变换,将两个子节点变成黑色,将xpp变成红色,然后将红色节点x顺利的添加到了xp的后面。
// 这里大家有疑问为什么将x = xpp?
// 这是由于将xpp变成红色以后可能与xpp的父节点发生两个相连红色节点的冲突,这就又构成了第二种旋转变换,所以必须从底向上的进行变换,直到根。
// 所以令x = xpp,然后进行下下一层循环,接着往上走。
if ((xppr = xpp.right) != null && xppr.red)
{
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 进入到这个else里面说明。
// 父节点xp是祖父的左节点xppr。
// 祖父节点xpp的右节点xppr是黑色节点或者为空,默认规定空节点也是黑色的。
// 下面要判断x是xp的左节点还是右节点。
else
{
// x是xp的右节点,此时的结构是:xpp左->xp右->x。这明显是第二中变换需要进行两次旋转,这里先进行一次旋转。
// 下面是第一次旋转。
if (x == xp.right)
{
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 针对本身就是xpp左->xp左->x的结构或者由于上面的旋转造成的这种结构进行一次旋转。
if (xp != null)
{
xp.red = false;
if (xpp != null)
{
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
// 这里的分析方式和前面的相对称只不过全部在右测不再重复分析。
else
{
if (xppl != null && xppl.red)
{
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
} else
{
if (x == xp.left)
{
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null)
{
xp.red = false;
if (xpp != null)
{
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
测试过程及遇到的问题
- 问题1: 无任何记录。
- 解决:
分析总结
代码托管











 浙公网安备 33010602011771号
浙公网安备 33010602011771号