20172319 《程序设计与数据结构》 第一周学习总结
20172319 2018.09.03-09.09
《程序设计与数据结构》第1周学习总结
目录
教材学习内容总结
第一章 概述：
-
1.1 软件质量： 软件符合明确叙述的功能和性能需求、文档中明确描述的开发标准、以及所有专业开发的软件都应具有的和隐含特征相一致的程度。
软件质量的特征： 1.正确性：软件在多大程度上满足其特定需求；
2.可靠性：软件故障发生的频率及危险程度；
3.健壮性：出错情况下可以得到处理的程度；
4.可用性：用户学习和执行任务的难易程度；
5.可维护性：对软件进行修改的难易程度;
6.可重用性：软件组件可重用于其他软件系统开发的难易程度；
7.可移植性：软件组件可以在多个计算机环境下使用的难易程度；
8.运行效率：在不浪费资源的情况下软件完成其目标的程度。 -
1.2 数据结构： 计算机存储数据的方式。
第二章 算法分析：
-
2.1 算法效率分析： 算法分析（analysis of algorithms）是计算机科学的一个基础，涉及多种技术和概念。
决定一个程序运行速度的主要因素是为完成某一特定任务所使用的算法的效率。 -
2.2 增长函数与大O记法：
增长函数（growth function）表示问题（n）大小与我们希望最优化的值之间的关系。该函数表示了该算法的时间复杂度（time complexity）
与空间复杂度（space complexity）。
渐近复杂度（asymptotic complexity），也称为算法的阶次(order)，是我们主要关注点。
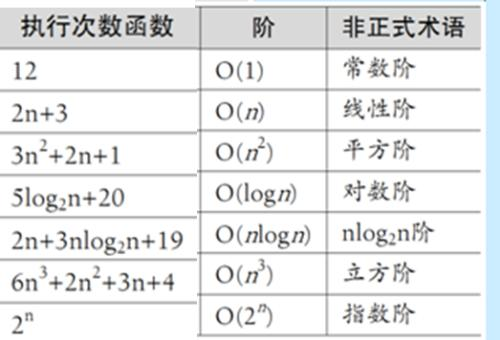
大O记法：用O（阶次）来表示某一算法具有某一阶次的时间复杂度的方法。
-
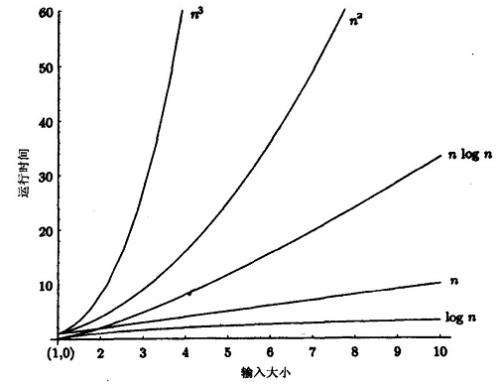
2.3 增长函数的比较：
-
2.4 时间复杂度分析：
1.循环运行的时间复杂度分析：循环体的复杂度乘以该循环的运行次数。
时间复杂度：O（n）
for (int count = 0; count < n; count++)
{
// 复杂度为O(1)的步骤系列
}
时间复杂度：O（logn）
count = 1;
while(count < n)
{
count *=2;
//复杂度为O(1)的步骤系列
}
2.嵌套循环的时间复杂度分析：内外层循环均需考虑。
内层循环的复杂度O（n），外层循环运行次数：n，总复杂度O(n^2)
for(int count = 0;count < n;count++)
{
for(int count2 = 0;count2<n;count2++)
{
//复杂度为O(1)的步骤系列
}
}
3.方法调用的复杂度分析：具体问题具体分析。
时间复杂度：O（n^2）
for(int count = 0;count<n;count++)
{
printsum(count);
}
public void printsum(int count)
{
int sum = 0;
for(int I = 1;I<count;I++)
sum += I;
System.out.println(sum);
}
教材学习中的问题和解决过程
-
问题EX2.1: 下列增长函数的阶次是多少？
a.10n^2 + 100n +1000
b.10n^3 -7
c.2n+100n3
d.n^2logn -
解决：由大O记法以及渐近复杂度的定义可知：阶次与主项有关；所以应取n变化时，变换最快的一项作为主项。
a.n^2
b.n^3
c.2^n
d.n^2logn -
问题EX2.4：确定下面代码段的增长函数和阶次：
for (int count = 0; count < n; count++)
for(int count2 = 0 ; count2 < n; count2 = count2 + 2 )
{
System.out.println(count,count2)
}
-
解决：内层循环为n/2,外层循环次数n，增长函数为n2/2;时间复杂度为：O（n2）,阶次为n^2.
-
问题EX2.5：确定下面代码段的增长函数和阶次：
for (int count = 0; count < n; count++)
for(int count2 = 1 ; count2 < n; count2 = count2 * 2 )
{
System.out.println(count,count2)
}
- 解决：内层循环为（log2n ）- 1，外层循环为n，增长函数为 ： （nlog2n ）- 1时间复杂度O（nlog2n），阶次：nlog2n。
代码调试中的问题和解决过程
- 问题1：
- 解决：
代码托管
上周考试错题总结
- 错题1：
结对及互评
点评过的同学博客和代码
- 本周结对学习情况：
- 20172316赵乾宸
- 博客中值得学习的或存在问题：
- **博客中值得学习的或存在问题： **
其他（感悟、思考等，可选)
学习进度条
| 代码行数（新增/累积） | 博客量（新增/累积） | 学习时间（新增/累积） | 重要成长 | |
|---|---|---|---|---|
| 目标 | 3000行 | 15篇 | 300小时 | |
| 第一周 | 0/0 | 1/1 | 12/12 | 百废待兴 |
