计算几何——快速排斥实验和跨立实验
两条线段有且仅有一个公共点,且这个点不是任何一条线段的端点时,称这两条线段是严格相交的。
也就是说线段不严格相交时可以将端点作为交点,但本文不讨论不严格相交,只讨论严格相交的情况(即使它们在算法实现上差别不大)。
在判断两条线段是否相交时,我们常用快速排斥实验跟跨立实验这两种方法,快速排斥实验能很快的排除掉线段不相交的情况,但并没法成为线段相交的充要条件,在快速排斥实验之后接上跨立实验就能完全的判断两线段是否相交,但其实只用跨立实验这一种办法也能作为判断线段相交的充要条件。
1.快速排斥实验:
假设以线段P1,P2为对角线作一矩形R,再以Q1,Q2为对角线作矩形T,当两个矩形不相交的时候两条线段肯定不相交,即线段相交的必要条件时矩形相交。

P1坐标为(p1x,p1y),P2坐标为(p2x,p2y),Q1的坐标为(q1x,q1y),Q2的坐标为(q2x,q2y)。
那矩形相交的条件就是:
min(p1x,p2x) <= max(q1x,q2x) &&
min(q1x,q2x) <= max(p1x,p2x) &&
min(p1y,p2y) <= max(q1y,q2y) &&
min(q1y,q2y) <= max(p1y,p2y);
编程里只要写出min(int a,int b)跟max(int a,int b)这两个函数,再将上面的条件放进if() 语句就能初步确定线段有没有相交的可能性。
2.跨立实验:
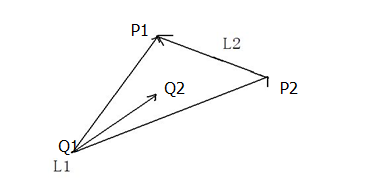
如果一条线段P1P2跨过了线段Q1Q2,那么P1,P2就分布在线段Q1Q2的两边,那么((P1-Q1)×(Q2-Q1))*((Q2-Q1)×(P2-Q1))>0 【此为条件1】。注意“×”是叉乘的意思,而“*”才是点乘。
(P1-Q1)×(Q2-Q1)能得出线段Q1P1跟线段Q1Q2叉乘结果的向量的方向,(Q2-Q1)×(P2-Q1)同样也会得出线段Q1Q2和线段Q1P2叉乘结果的向量的方向,只有这两个结果向量的点乘结果大于0,即这两个结果向量的方向一致时,P1,P2才会分布在线段Q1Q2的两边。
同理Q1Q2分布在P1P2两边的条件为((Q1-P1)×(P2-P1))*((P2-P1)×(Q2-P1))>0【此为条件2】。
同时满足以上两个条件时,线段Q1Q2跟线段P1P2才会相交。(其实只要满足这一个实验,两线段相交情况就能确定了,不需要前面的快速排斥实验)
编程里将以上公式转化为坐标运算就可以了,这里附上叉积公式:a × b = (l,m,n) × (o,p,q) = (mq-np,no-lq,lp-mo)
因此条件1等价于:[(P1x-Q1x)*(Q2y-Q1y)-(P1y-Q1y)*( Q2x-Q1x)] * [(Q2x-Q1x)*(P2y-Q1y)-(Q2y-Q1y)*(P2x-Q1x)] > 0
条件2等价于:[(Q1x-P1x)*(P1y-P2y)-(Q1y-P1y)*( P2x-P1x)] * [(P2x-P1x)*(Q2y-P1y)-(P2y-P1y)*(Q2x-P1x)] > 0
将以上两个表达式写入if()语句即可判断线段相交与否。
注:上面两张图都不是自己画的,直接百度来的,算是盗图吧。


