归并排序

 

主要参考：归并排序的C++实现

 

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

以上内容来自百度百科。

 

归并排序主要分为两部分：

1、划分子区间

2、合并子区间

 

现在以 9,6,7,22,20,33,16,20 为例讲解上面两个过程：

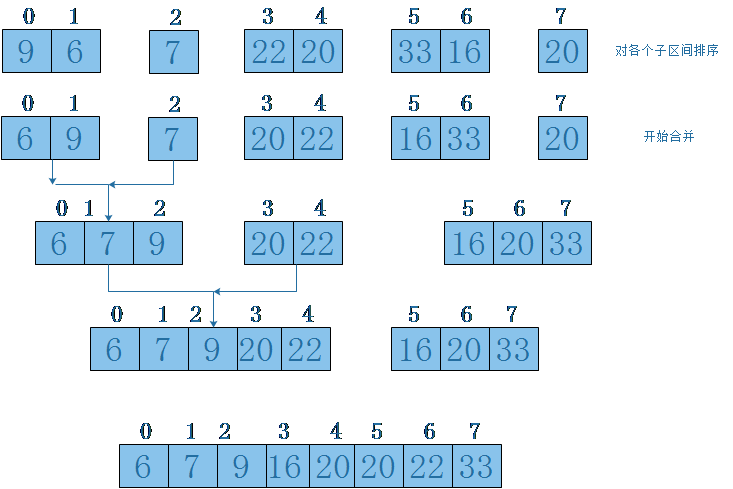
第一步，划分子区间：每次递归都从中间把数据划分为左区间和右区间。

原始区间为[start,end],start=0,end=[length-1]，减一是因为数组的下标从0开始，本例中length=8,end=7。现在从中间元素划分，划分之后的左右区间分别为 [start,(end-start+1)/2+start]，右区间为[(end-start+1)/2+start+1,end]，本例中把start和end带入可以得到[0,7]，划分后的左右子区间为[0,4],[5,7]，然后分别对[start,end]=[0,4]和[start,end]=[5,7]重复上一步过程，直到每个子区间只有一个或者两个元素。

整个分解过程为:

 

子区间划分好以后，分别对左右子区间进行排序，排好序之后，在递归的把左右子区间进行合并，整个过程如下图所示：

 

 

 

代码：

void mergeSubArry(vector<int> &a, int st, int ed, vector<int> &r)
{
    int st1=st;
    int ed1=(st+ed)/2;
    int st2=ed1+1;
    int ed2=ed;
    int rInd=st;
    //r[st]~r[ed]为合并后的序列;
    while(st1<=ed1 && st2<=ed2)
    {
        if (a[st1]<a[st2])
        {
            r[rInd++]=a[st1++];
        }
        else
        {
            r[rInd++]=a[st2++];
        }
    }
    while (st1<=ed1)
    {
        r[rInd++]=a[st1++];
    }
    while(st2<=ed2)
    {
        r[rInd++]=a[st2++];
    }

    //注意，不要忘记把合并后的序列复制到原数组中，因为每次二路合并操作的都是之前合并好的子序列;
    for (int i=st;i<=ed;i++)
    {
        a[i]=r[i];
    }
}

void corefun(vector<int> &a,int st,int ed, vector<int> &r)
{
    //划分子数组;
    if (ed-st<1)//若划分子序列至一个元素，结束当前划分;
    {
        return ;
    }
    if (ed-st==1)//若划分子序列至两个元素，排序后结束后当前划分;
    {
        if (a[ed]<a[st])
        {
            swap(a[st],a[ed]);
        }
        return ;
    }
    int mid=(st+ed)/2;
    corefun(a,st,mid,r);
    corefun(a,mid+1,ed,r);

    //合并子数组;
    mergeSubArry(a,st,ed,r);

    //把合并后的序列复制到原数组中也可以在此处操作;
    /*for (int i=st;i<=ed;i++)
    {
        a[i]=r[i];
    }*/

}


void mergeSort(vector<int> &a)
{
    int size=a.size();
    vector<int> r=a;
    corefun(a,0,size-1,r);
}

 

下面进行测试，测试代码如下，输入【1,4,3,2,5,8,7,6】：

 

void main()
{
    vector<int> test1;
    test1.push_back(1);
    test1.push_back(4);
    test1.push_back(3);
    test1.push_back(2);
    test1.push_back(5);
    test1.push_back(8);
    test1.push_back(7);
    test1.push_back(6);

    mergeSort(test1);

    cout<<"排序后的数组："<<endl;
    for (int i=0;i<test1.size();i++)
    {
        cout<<test1[i]<<" ";
    }
    cout<<endl;
}

 

 输出：

 

PS：最开始实现时没有在merge函数中将合并好的子序列拷贝赋值到原数组中，而是直接在最后的sort函数中将r中元素拷贝给a数组，导致结果错误。原因是，每次merge中合并的序列都应该是之前合并好的序列，而不是未经改变的原始数组。

 

 

 其他参考：常见排序算法C++总结

 

代码优化：划分子序列时，可以直接划分到一个元素。另外，还可以少定义一个函数，直接将合并序列部分与划分序列部分放到一个函数里（参数都相同）。

代码：

void sortfun(vector<int> &a,int st,int ed, vector<int> &r)
{
    //划分子序列，若划至只有一个元素，结束划分;
    if (ed-st<1)
    {
        return ;
    }

    int mid=(st+ed)/2;
    int st1=st;
    int ed1=mid;
    int st2=mid+1;
    int ed2=ed;
    
    sortfun(a,st1,ed1,r);
    sortfun(a,st2,ed2,r);

    //合并子数组,r[st]~r[ed]为合并后的序列;
    int rInd=st;
    while(st1<=ed1 && st2<=ed2)
    {
        if (a[st1]<a[st2])
        {
            r[rInd++]=a[st1++];
        }
        else
        {
            r[rInd++]=a[st2++];
        }
    }
    while (st1<=ed1)
    {
        r[rInd++]=a[st1++];
    }
    while(st2<=ed2)
    {
        r[rInd++]=a[st2++];
    }

    //注意，不要忘记把合并后的序列复制到原数组中，因为每次二路合并操作的都是之前合并好的子序列;
    for (int i=st;i<=ed;i++)
    {
        a[i]=r[i];
    }
}


void mergeSort(vector<int> &a)
{
    int size=a.size();
    vector<int> r=a;
    sortfun(a,0,size-1,r);
}