算法专题——整除同余(数论汇总)

整除同余

基本把数论过了一遍，来写几篇博客再梳理一遍。

第一部分 围绕四个中心

一、素数

素数，指的是在大于1的自然数中，除 1 和它本身之外没有其他约数的数。1不是素数。

素数是数论中很重要很特殊的一类数。

1. 从素数的定义上来看，素数与其他整数在”可否整除“上做出了区分，”可否整除“对应数论中的”整除同余“，而”整除同余“在数论中具有非常重要的地位。所以素数在数论中是非常重要的一类数。
2. 从最大公约数（下面会介绍）的角度上看，素数与比自己小的数字总是互质(GCD == 1)，满足一些定理的成立条件，写题时可以无脑使用相对应的定理。但还是需要多加注意一些定理中一些容易忽视的坑，譬如素数与自己大的数不总是互质的。
3. 从质因数分解上看，素数只能分解为自己本身，在几何表达时只占众多格子中的一个(具体解释在下面)。
4. 从分布上看，n以内的素数大概有$n/ln\ n$个。

二、模运算，整除符号与同余方程

1. 模运算

是许多编程语言中都有定义的运算，在数论中，模运算个人理解主要是用于大数的小数化，将其限定在一定的数字范围内，方便处理。

2. 整除与同余

1. 整除：$a\mid b$​​​​​，a divide b，a(整)除b，是整除常见的三种表达方法（还有一些被动形式的表达，divided by，除以），其表达的含义用数学语言表达为：$b=k*a,其中k是整数,a数学上不能为0$。至于整除所涉及的一些特性，这里不过多赘述。
2. 同余：$a\equiv b(mod p)$​​，a和b对模p同余，英语的表达方式不记得了。同余与整除联系十分密切，其表达的含义用整除的方法表达为：$p\mid (a-b)$​，延续整除的概念，同余中$p$​一般也不为0。一些简单的性质这里不多赘述，只提一个我记得不太熟的结论：$若a \equiv x(mod\ p),a \equiv x(mod\ q),p与q互质,则a \equiv x(mod\ p∗q)$​​。
3. 符号问题：一般而言，整除中的除数（左边那个）的符号一般并不重要，取模运算的模数的符号一般也不重要，都不会影响结果的正确性；但当其出现在被除数以及被模数时要注意其符号的正确性。
4. 处理上：同余方程的求解以及后续处理中，一般习惯于将恒等号变为等号，结合数字的整除理论的特性进行后续处理。

3. 快速幂

一般快速幂

ll bin(ll x, ll n, ll mod) {
    ll ret = mod != 1;
    for (x %= mod; n; n >>= 1, x = x * x % mod)
        if (n & 1) ret = ret * x % mod;
    return ret;
}

大数快速幂（用于指数大于long long的数据），将其一位一位的快速幂然后相乘。

ll bin(ll x, ll n, ll mod) {
    ll ret = mod != 1;
    for (x %= mod; n; n >>= 1, x = x * x % mod)
        if (n & 1) ret = ret * x % mod;
    return ret;
}
ll bin(ll a,char *b,int len) {
    ll ans=1;
    while(len>0){
        if(b[len-1]!='0'){
            int s=b[len-1]-'0';
            ans=ans*bin(a,s,mod)%mod;
        }
        a=bin(a,10,mod);
        len--;
    }
    return ans;
}

int main(){
    char s[100050];
    int a;
    while(~scanf("%d",&a)) {
        scanf("%s",s);
        int len=strlen(s);
        printf("%I64d\n",bin(a,s,len));
    }
    return 0;
}

三、最大公约数

最大公约数(gcd)是描述两个数字之间的特性的一类数，最为特殊的最大公约数——1，表明了两个数字是互质的。$gcd(a,b)$​含义为绝对值最大的可以同时整除$a$和$b$​​的数。

1. 从定义上看，它给出了互质的数学表达，$gcd(a, b) = 1$​，这是很多定理成立的基础。在使用前应该注意是否成立。
2. 从质因数分解（下面会涉及）上看，它形如$GCD(a, b)=P1^{min(α1, β1)}*P2^{min(α2, β2)}*…P3^{min(α3, β3)}$​，而两个数的最小值这一表现形式在一些涉及gcd的性质上给出了更好的解释与说明，例如$gcd(a,b)*lcm(a,b)=a*b$，$gcd(a,b)=d\rightarrow gcd(a/d,b/d)=1$​。​​
3. 从数学表达上看：$gcd(a,b)=d$​​​​可以转化为3个整除式子，$d\mid a,d\mid b以及d\mid a-b$​​​​，​​对应地可以得到3个同余方程，这里不多赘述。这种数学表达在后续很多定理的证明中包括做题时都用得到。
4. 从定义域值域上看：a和b不能同时为0；当有一个为0时，其值为另一个数；当有一个为负时，其值符号不定；当两个同号时，其值也对应的是什么符号。

1. 最大公约数的求法

1.1辗转相除法

也叫欧几里得算法。

原理：$gcd(a, b)=gcd(a,b-a)$​，或者说更常见的表达式是$gcd(a,b)=gcd(b, a\%b)$​​​​​​​​。证明方法正是用到了上面提及的第三点，这里不多赘述。时间复杂度为：$O(log\ min(a,b))$，一般情况下比这个更小。​

代码实现如下：

inline ll gcd(ll a, ll b) {return !b ? a : gcd(b, a % b);}

1.2基于二进制优化的求法

原理不过多赘述，看代码吧

inline ll gcd(ll x, ll y) {
    int i, j;
    if (x < y) swap(x, y);
    if (y == 0) return x;
    for (i = 0; (x & 1) == 0; i++) x >>= 1;  // 去掉所有的 2
    for (j = 0; (y & 1) == 0; j++) y >>= 1;  // 去掉所有的 2
    while (1) {
        if (x < y) swap(x, y);				// 保证 x 大于等于 y
        if ((x -= y) == 0) return y << min(i, j);// 等于 0 表示另一部分因子为 y
        while ((x & 1) == 0) x >>= 1;         // 去掉所有的 2
    }
}

1.3基于值域预处理

原理还没细看，直接当模板用应该没啥问题，可以$O(1)$得到值

const M = 1e6, N = 1e3;
int prime[M+5], tot = 0;
int fac[M+5][3];
int gcd[N+5][N+5];
bool check[M+5];
// 线性筛分解 x 为 (a, b, c) 
void Sieve() {
    fac[1][0] = fac[1][1] = fac[1][2] = 1;
    for (int i = 2; i <= M; i ++) {
        if (! check[i]) {
            prime[++ tot] = i;
            fac[i][0] = fac[i][1] = 1, fac[i][2] = i;
        }
        for (int j = 1; j <= tot && i*prime[j] <= M; j ++) {
            int k = i*prime[j];
            check[k] = true;
            fac[k][0] = fac[i][0] * prime[j];
            fac[k][1] = fac[i][1], fac[k][2] = fac[i][2];
            if (fac[k][0] > fac[k][1]) swap(fac[k][0], fac[k][1]);
            if (fac[k][1] > fac[k][2]) swap(fac[k][1], fac[k][2]);
            if (i % prime[j] == 0) break;
        }
    }
}
// 预处理 N = sqrt(M) 内的 GCD
void init_gcd() {
    for (int i = 1; i <= N; i ++) {
        gcd[i][0] = gcd[0][i] = i;
        for (int j = 1; j <= i; j ++)
            gcd[i][j] = gcd[j][i] = gcd[j][i%j];
    }
}
// 接着求 GCD 就变成了这样 O(1)
int GCD(int a, int b) {
    int res = 1;
    for (int i = 0, r; i < 3; i ++) {
        if (fac[a][i] > N) {
            if (b % fac[a][i]) r = 1;
            else r = fac[a][i];
        }else r = gcd[fac[a][i]][b%fac[a][i]];
        b /= r;
     	res = res * r;
    }
    return res;
}

2. 最小公倍数

重要性不及最大公约数，所以将其放在了最大公约数的下面。

1. 与gcd具有性质：$gcd(a,b)*lcm(a,b)=a*b$​，其证明在质因数分解上很容易看出来。
2. 转化为gcd（以第一条为基础）：$lcm(a,b)=d\rightarrow gcd(a,b)=a*b/lcm(a,b)=a*b/d$

四、逆元

如果有$ax\equiv 1(mod\ n)$​​，则称$x$是模$n$意义下$a$的乘法逆元。记$x=inv(a)$或$x=a^{−1}$。

逆元的出现主要是为了完善同余方程下四则运算的完整性，我们知道同余方程下，等式两边同时做加减乘是比较容易的，但是除却是不被允许的，这主要是因为除法运算会产生小数，而小数是不被同余方程所允许的。

但除法很常见也很重要，于是想到了一种方法，如果一个小数在给定模数下有且仅有一个整数与之对应，我们便允许其存在，其等价的含义就是$a^{-1}$在模$p$下唯一对应一个整数。

当然这种对应不是乱对应的，其需要满足某些条件，我们要求对应的整数满足$a*a^{-1}\equiv 1(mod\ n)$（这样定义逆元可以使我们更加方便地完成相关计算），这时我们便称$a^{-1}$是模$p$下的$a$​的逆元。

至于逆元的求法，主要有三种，一种是费马小定理，一种是拓展欧几里得，一种是线性求。这里只介绍第三种，至于第一第二种下面会介绍。

线性求

要求p是素数，且所求的数不超过该素数。

原理：

其中$(p\%i)^{-1}$​​​是已知的​，于是就可以线性求出来了。​

//预处理
inv[1] = 1;
for (int i = 2; i < P; i ++)
	inv[i] = (P - P/i) * inv[P%i] % P;

第二部分 重要定理

从处理的对象的个数上，可以将其分为两个部分，一个是针对一个数字的，另一个是针对两个及多个数字的。

针对一个数字的，有数字的质因数分解，整除操作。

针对两个及多个数字的，主要是同余方程，以及相关的变形应用。

一、 整数的唯一分解定理

任意的正整数都有且只有一种方式写出其素因子的乘积表达式。$A = p_1^{k_1}p_2^{k_2}p_3^{k_3}…p_n^{k_n}$​ ，其中 $p_i$均为素数。

证明上可以假设其有两个分解，然后通过质数的性质推导出其矛盾。

1. 质因数分解，为一个整数的约数提供了几何化的表达，为整数的约数问题提供了排列组合的模型，提供了一种新的思路与视角，许多定理的证明与性质的证明在质因数分解的角度上看都会显得不言自明，简单明了。他将一个数字拆分成了一组质数的乘积，而这一组的质数的不同组合的乘积可以得到这个数字的一个约数，一组数的不同组合这一点正是体现了组合数学的特点。

下面的几个点均体现了上面所提到的特点。

1. 约数个数

对于整数 $A = p_1^{k_1}p_2^{k_2}p_3^{k_3}…p_n^{k_n}$​，其因子个数为：$T=(1+k_1)*(1+k_2)*…*(1+k_n)$​。

对于每一个质因数，均有取0个到取k个的k+1种选择，根据乘法原理，总的个数便是上式所表达的个数。

2. 约数和

对于整数$A = p_1^{k_1}p_2^{k_2}p_3^{k_3}…p_n^{k_n}$，其所有因子之和为：$S=(1+p_1+p_1^2+…+p_1^{k_1})*(1+p_2+p_2^2+…+p_2^{k_2})*…*(1+p_n+p_n^2+…+p_n^{k_n})$。

类比卷积，可以发现每一个因子都会被表达出来（结合质因数分解以及排列组合显然可以得到）。

至$(1+p_1+p_1^2+…+p_1^{k_1})$​的求法，可以用递归二分的方法求，这里只给出模板，公式就不多赘述了。

ll bin(ll x, ll n, ll mod) {
    ll ret = mod != 1;
    for (x %= mod; n; n >>= 1, x = x * x % mod)
        if (n & 1) ret = ret * x % mod;
   	return ret;
}
ll sum(ll p, ll n) {  // 求 1 + p + p^2 + …… + p^n
    if (n == 0) return 1;
    if (n & 1) return sum(p, n/2) * (1 + bin(p, n/2+1, MAXLL));
    return sum(p, n/2 - 1) * (1 + bin(p, n/2 + 1, MAXLL)) + bin(p, n/2, MAXLL);
}

3. 莫比乌斯反演

莫比乌斯反演是基于约数关系的定理，关于其正确性的证明就是用到了容斥原理，所以在一些需要用到莫比乌斯反演的题目中，考虑普通的容斥原理实际上也可以解出思路得到答案，当然复杂度可能不如莫比乌斯反演这么优。

二、整除操作\整除分块

1. 整除操作

在这里提到整除分块可能觉得有些突兀，其实这里想强调的是$n/i$​​，以及所有带有整除运算的计算结果所代表的含义。

1. 一个除的，$n/i$​​，如果将$i$​​​视为一个块的大小，其可以表示为能将$n$​分为完整的几块；如果将$i$视为一个约数，则其可以表示为$1\sim n$中，有多少个数包含$i$​​这个因子。
2. 一个除的，对于不是求$1\sim n$范围，而是$a\sim b$范围的，可以使用前缀和的思想，但是这时候需要需要考虑$a\%i$的大小来决定是使用$a/i+1$还是$a/i$，当$a\%i=0$时，为$b/i - a/i + 1$个；反之为$b/i-a/i$​。
3. 两个除的，$n/(n/i)$​​​​，整除分块的理论，其值为取到与$i$​​​位置的值相同的最大位置，具体见下。

2. 整除分块

整除分块用于求所有形如$\sum_{i = 1}^n\lfloor n/i \rfloor$​​的式子的$O(\sqrt n)$​​计算的。

$\lfloor n/i \rfloor$的值$val$，可以形象的理解为在$i$这个位置可以放的最大值$val$，使得$val*x \leq n$成立。可以发现许多情况下，连续的一片位置所能放置的最大值都是相同的，所以如果我们能找到一片区域的值全是相同的，我们就可以不用一个个计算其值再将其加起来，即找到一片区域$[l,r]$的值都为$val$，对与整个式子的贡献就可以很快的算出为$(r-l+1)*val$。

延续上面除法运算带来的最大的特点，自然的$n/(n/i)$​​​就表示，可以放置值为$n/i$​​的最大位置为多少。

所以就可以得到$[l,\ n/(n/l)]$​区间中的值都是相等的。

继而通过可以将$n$​​分为不同的$\sqrt n$​​​块（证明略），具体实现如下：

for(int l=1,r;l<=n;l=r+1) {
	r=n/(n/l);
	ans+=(r-l+1)*(n/l);
}

三、素数筛法

1. 埃氏筛

合数总是可以分解为质数的积，只要将要求的范围内已经求出的所有质数的倍数都去掉，剩下的就是质数。

const int N = 1e6 + 5;
int p[N], cnt;
bool isp[N];
void make_prime(int n = N - 5) {
    memset(isp, true, sizeof(isp));
    isp[0] = isp[1] = false;
    for (int i = 2; i <= n; i ++) {
        if (! isp[i]) continue;
        p[++ cnt] = i;
        for (int k = i*i; k <= n; k += i) 
            isp[k] = true;
    }
}

2. 欧拉筛

基于整数唯一分解定理而来，将一个合数数字的质因数分解的结果拆分为两组（合数的拆分结果的质数个数一定大于两个），一组只包含一个最小质因数，另一组则包含剩下的质因数，这样合数可以通过$prime*i$来唯一的表达任意一个合数，我们便通过这样的方式将所有的合数全部筛掉，剩下的没有被筛掉的即为不能表达为$prime*i$​的形式的数字，即为质数。

ll pr[MAXN], p_sz;
bool vis[MAXN];
void getPri(int n) {
	for (int i = 2, d; i <= n; i++) {
		if (!vis[i]) pr[++p_sz] = i;
		for (int j = 1; j <= p_sz && (d = i * pr[j] < MAXN); j++) {
			vis[d] = true;
			if (i % pr[i] == 0) break;
		}
	}
}

上面给出的代码的第八行便是起到了使得每一个形如$prime*i$的合数都只被筛选一次的关键，第二层循环是枚举比$i$小的所有质数，所以当遇到$i\ \%\ pr[i] == 0$​​还继续枚举的话，$prime*i$中$prime$​是最小的质因数的前提就不成立了，就会造成重复筛数。

3. 区间筛

用于筛出给定的区间有哪些是素数的筛法，当数据范围为这样的时候：$[L,\ R]$​，区间长度为$R-L+1 \le 10^6,\ L,\ R\le 10^{12}$，就需要用到区间筛法。

原理也非常简单，一个大数，如果是合数，比如$n$​，则一定包含一个小于$\sqrt n$的因子，所以可以枚举所有小于$\sqrt n$​的素数，来筛掉区间内的合数，区间中剩下的未被筛掉的便是质数。​​​

if (L == 1) L = 2; // 特判，1 不是质数也不是合数
memset(isp, false, sizeof(isp));
for (int i = 1; i <= cnt; i ++) {
    ll P = p[i], s = (L + P - 1) / P * P; // s 为起点
    if (s < 2 * P) s = 2 * P;
    for (ll j = s; j <= R; j += P) 
        isp[j-L+1] = true; // 减去L-1相当于做了个简单哈希
}

四、Miller-Rabin素数探测

五、拓展欧几里得算法

扩展欧几里得算法是用来在已知(a, b)$时，求解一组(x, y)，使得ax+by=GCD(a,b)。

拓展欧几里得算法既证明了上式是一定有解的，也给出了解的求解过程。

1. 内容

拓展欧几里得算法内容如下：

$ax+by=GCD(a,\ b)=GCD(a,\ a\ mod\ b)=ax'+(a\ mod\ b)y'$

然后我们证明如果左边两个式子存在解时，右边的两个式子也存在解。

$ax+by=bx'+(a−a/b*b)y'=bx'+ay'−(b*a/b)y'=ay'+b(x'−a/b*y')$​

由待定系数法，得到$\begin{cases}x=y′\\y=x′−a/b*y′ \end{cases}$

即当右边两式成立时，左边两式也成立，且其中一组值的对应关系如上。

所以我们可以模拟辗转相除法的过程，递归的将$ab$不断变小。递归基为$b=0$，此时得到一组解为$\begin{cases}x=1\\y=0 \end{cases}$

而后在回溯过程中将$xy$​​不断的往回代即可得到一组合法的解，代码实现如下。

inline ll ex_gcd(ll a, ll b, ll &x, ll &y) {
    if(b == 0) { x = 1, y = 0; return a;}
    ll r = ex_gcd(b, a % b, y ,x);
    y -= a / b * x;
    return r;
}

2. 性质

1. 若通过扩展欧几里得求出一组特解$(x_0,y_0)$​​，即$ax_0+by_0=gcd$​​。

   则方程的通解为：$\begin{cases} x=x_0+k*(b/gcd) \\ y=y_0-k*(a/gcd) \end{cases}$

2. 已知ax+by=d的解，对于ax+by=c的解，c为任意正整数，只有当d|c时才有解。

   其通解为： $\begin{cases} x=(c/gcd)x_0+k*(b/gcd) \\ y=(c/gcd)y_0-k*(a/gcd) \end{cases}$​​

3. 常见应用

1. 求形如ax+by=c的通解，或从中选取某些特解
2. 求乘法逆元
3. 求解线性同余方程（本质上和第一点没有区别）

六、中国剩余定理

1. 内容

$$S: \begin{cases} x\equiv r_1\ (mod\ m_1) \\ x\equiv r_2\ (mod\ m_2) \\ ...\\ ...\\ x\equiv r_n\ (mod\ m_n) \\ \end{cases}$$

假设整数 $m_1,\ m_2,\ …,\ m_n$两两互质，则对任意的整数：$a_1,\ a_2,\ …,\ a_n$​​，方程组 S 有解，并且解以以下形式给出：

$x=(\displaystyle\sum_{i=1}^n a_i t_i M_i)\ mod\ M$​，其中$M=\prod_{i=1}^{n}m_i$​，$M_i=M/m_i$​，$t_i=M_i^{-1}\ (mod\ m_i)$​​​。

证明$x$是其中一个解，可以直接将$x$往回代即可。而要证明$x$是所有的解的通解，则可以结合整除运算和素数的特点进行证明，这里不多赘述。

实现代码如下：

ll CRT(ll *a, ll *m, ll n) {
    ll M = 1, ans = 0;
    for (int i = 1; i <= n; i ++) 
        M *= m[i];
    for (int i = 1; i <= n; i ++) {
        ll Mi = M / m[i], t, y;
        exgcd(Mi, m[i], t, y); 			// Mi * t = 1 (mod m[i])
        t = (t % m[i] + m[i]) % m[i];
        // ans += a[i] * t * Mi
        ans = (ans + fmul(fmul(a[i], t, M), Mi, M)) % M;
    }
    return ans;
}

2. 拓展中国剩余定理

$$S: \begin{cases} x\equiv a_1\ (mod\ m_1) \\ x\equiv a_2\ (mod\ m_2) \\ ...\\ ...\\ x\equiv a_n\ (mod\ m_n) \\ \end{cases} \rightarrow \begin{cases} x\equiv ans\ &(mod\ lcm(m_1, m_2)) \\ x\equiv a_3\ &(mod\ m_3) \\ ...\\ x\equiv a_n\ &(mod\ m_3) \\ \end{cases} \rightarrow x\equiv ans\ (mod\ lcm(m_1,\ ...,\ m_n)) \\ $$

求解的过程是迭代的过程，可以分为以下几步：

1. 考虑中间的迭代过程 $x \equiv ans (mod\ lcm)$，只考虑前面已经迭代的$i-1$个方程的话，$x$的答案显然就是$ans + k*lcm$。
2. 现在考虑合并下一个方程$x \equiv ai(mod\ mi)$。思路很直接，让前$i - 1$个方程同样兼容第$i$个方程即可。一种朴素的思路，将$ans + k*lcm$代入到第二个式子中，得到合法的$k’$（这里只要求出来一个即可），则其中一个解即为$ans+k'*lcm$，通解为$ans+k'*lcm+t*lcm'$（这里的lcm’是新的模数）
3. 所以接下来要得到一个合法的$k'$​​，可以使用拓展欧几里得定理求解，得到方程$x*lcm + y*mi=ai-ans$​​（这里用$x$​​来代替$k'$​​，表示解出的$x$​​即为我们要求的$k$​​）；通过拓展欧几里得定理可以知道，假设解出来的其中一个特殊解为$x0$​​，则通解的形式为$x0+k''(pi/gcd)$​（这里的$k''$等同于$k$，仅是为避免混淆修改了一下）；将通解带回第一个原表达式，即$ans+k'*lcm$中的$k'$，可以得到其解即为$x=ans+k'*lcm+t*lcm'$​(即上面提到的模式，在这里我们通过拓欧求出来这个表达式)，这里的$k'$即为$x0$是定值，t是整数变量等同于k，这里的$lcm'$就是$lcm(lcm, pi)$。可以发现这个解是既满足第一个表达式也满足第二个表达式的，成立。
4. 以上就是求解的过程，再梳理一遍：已经有前$i-1$个方程的通解，找到符合第$i$个方程的通解需要找到一个特殊的$k$​，将其求出来之后就可以得到满足前$i$​个方程的通解了。
5. 有几个点需要注意，求解同余方程的过程中是针对于pi同余的，所以A和C需要对B，即mi取模（ABC的含义：$Ax+By\equiv C$）。求解得到的$x$的通解是在$B/gcd(A, B)$的基础上得到，求x的最小正整数解的时候要注意。$ans$的通解是在$lcm(A, B)$​的基础上得到的，这里要注意分辨。​
6. 更加一般的思想，将两个同余方程合并在一起，就是求解有哪些答案，即满足第一个同余式，又满足第二个同余式的过程，几乎都逃脱不出拓展欧几里得求答案的过程。

实现代码如下：

pair<bool, ll> exCRT(ll* r, ll* m, ll n) {
    ll x, y, ans = r[0], M = m[0];
    for (int i = 1; i < n; i ++) {
        ll a = M, b = m[i], c = (r[i] - ans%b + b) % b;
        ll d = exgcd(a, b, x, y), q = b/d;
        if (d == 0 || c % d) return make_pair(0, 0);
        x = fmul(x, c/d, q);
        ans += x * M, M *= q;
        ans = (ans%M + M) % M;
    }
    return make_pair(1, (ans%M + M) % M);
}

七、欧拉定理

1. 欧拉函数

$φ(n)$​​，小于等于n的所有数中与n互质数的个数

欧拉函数的一般求法：$\frac{φ(n)}{n}=\prod_{p\mid n}(1-\frac{1}{p})$​；

1.1 证明过程：

证明可以大致分为三个步骤，首先证明$φ(p)=p-1$，然后证明$φ(p^k)=p^k-p^{k-1}$，最后证明$φ(p_1^{k_1}p_2^{k_2})=φ(p_1^{k_1})φ(p_2^{k_2})$，可以发现还是通过质因数分解结合容斥原理得到这个结论的。三个步骤的具体阐述这里就不给出了。

1.2 欧拉函数具有的一些性质

1. 如果正整数$n>2$，那么$φ(n)$​​ 是偶数。
2. 如果$n\ |\ N$​，那么$φ(n)\ \mid\ φ(N)$​ 。
3. 对于正整数$m$, $n$有$φ(mn)=φ(m)φ(n)\frac{GCD(m, n)}{φ(GCD(m, n))}$​。
4. 特别的，如果$m$, $n$互质，那么$φ(mn)=φ(m)φ(n)$ 。
5. 对于正整数$n$有 $\displaystyle\sum_{d\ |\ n}\varphi(d) = n$。
6. 对于正整数$n$有$\displaystyle\sum_{1\le k\le n, \ GCD(k,\ n) = 1} \frac{k}{n} = \frac{\varphi(n)}{2}$​​。

1.3 待补充

欧拉函数给出了$n$以内满足$gcd(a,\ b)=1$的$a$的个数这在许多，求gcd的和的题中作用比较大，至于更多的其他方面的应用，由于做题数量还不是特别多，所以并不是特别清楚，之后题目做多一点后来补充。

2. 欧拉定理

欧拉定理，如果$gcd(a, n)=1$​​，则有$a^{φ(n)}\equiv 1\ (mod\ n)$​

2.1 证明​

证明的过程涉及到了剩余系的概念，不过其实从质因数分解提供的几何化表达上也可以很自然的去理解。

考虑模n的最小正缩系 $φ_n= \{c_1,\ c_2,\ …,\ c_{ϕ(n)}\}$，已知 $GCD(a,\ n) = 1$ ，我们在 $ϕ_n$的每一个元素面前都乘以一个 a，得到$aϕ_n= \{ac_1,\ ac_2,\ …,\ ac_{ϕ(n)}\}$。利用反证法或者从质因数分解提供的几何化表达上可以得到$aϕ_n$也是一个模$n$的缩系。

则可以得到：

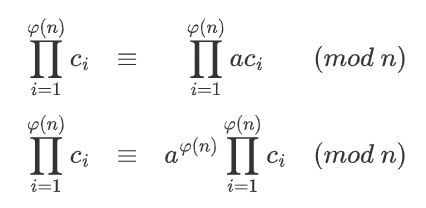
得到$GCD(n, \prod_{i=1}^{φ(n)}c_i)=1$，所以可以两边消去之后，可以得到$a^{φ(n)}\equiv 1\ (mod\ n)$​​ 。得证。

2.2 拓展欧拉定理

对于$a$与$n$不互质的情况也做出了描述，给出了完整的公式。注意第二个式子的$x$不能为负数。

$$a^x\equiv \begin{cases} a^{x\ mod\ φ(m)} & GCD(a,\ m) = 1 \\ a^{x\ mod\ φ(m) + φ(m)} & GCD(a,\ m) ≠1, x \ge φ(m) \end{cases} \ (mod\ m)$$

可以简单的理解为欧拉定理总是可以将指数缩小到两倍$φ(m)$内，当$m$与$a$互质时，可以将这一差距缩小到一倍$φ(x)$​以内。

欧拉定理表明了如果$a$与$m$互质，在模$m$的情况下，$a^{φ(m)}$的值与1是相同的，所以可以知道在高次计算中，$φ(m)$一定是指数的一个循环节，当然并不一定是最小的循环节，但最小的循环节一定是$φ(m)$的一个因子，证明方法可以参考字符串那里。

2.3费马小定理

欧拉定理的一个特例，即当模数$p$是质数，且a，p互质时，有$a^{p-1}\equiv1\ (mod\ p)$。用来求逆元很方便。​

八、BSGS算法

求满足$a^x\equiv y\ (mod\ p)$​的最小自然数x或报告无解，其中$a$​与$p$​互质。

1. 内容

基于欧拉定理提出的一个算法，用于求解高次同余方程的一个解。从欧拉定理可以，模$p$​​意义下指数$x$​​满足一个循环节，如果可以将循环节内可能的值全部枚举一遍，找到一个符合的$x$​​，就求出了我们想要的原式的解。所以相比其他算法与定理而言，BSGS显得就有些粗暴不够优美，但是其枚举的方法上却可以给我们带来很大的启发意义，其枚举的特点便是大步小步，时间复杂度可以得到$O(\sqrt p\ log\ p)$​​或$O(\sqrt p)$​​级别。

BSGS的思路很简单，就是如何尽快的在$φ(p)$​范围内枚举到一个$x$​，使得$a^x\equiv y\ (mod\ p)$​。

首先考虑朴素的枚举方法，如果从$1\sim φ(P)$一个个枚举，那么如果$p$是质数时，时间复杂度回达到$O(p)$的级别。

考虑我们在哈希表中学到的知识（用哈希的方法求解方程的解是很经典的一类问题）。将$x$​​分成两块两个变量，放在等式两边，枚举其中一边的变量，将得到的值存储在哈希表中，而后再枚举另一边的值，如果能与哈希表中的值匹配的上，那么就表示有正确答案，反之则表示没有。这样两遍枚举之后就可以将所有可能的$x$​都枚举完了，而一次枚举的时间复杂度就是$O(\sqrt p)$，下面说明如何拆分可以使枚举时间复杂度开根。

另$x=km-r$，其中$k$和$r$就是拆分出的两个变量，$k$的定义域为$1,\ 2,\ ...,\ \lceil \frac{p}{m} \rceil$，$r$的定义域为$1,\ 2,\ ...,\ m-1$，$m$是认为设置的常量，得到$a^{km}\equiv y*a^r\ (mod\ p)$，左边枚举完之后，枚举右边，时间复杂度就是$O(\lceil \frac{p}{m} \rceil+m-1)$，容易得到$m=\sqrt p$时，时间复杂度最低，为$O(\sqrt p)$。以上便是如何将枚举的时间复杂度开跟的过程。

所谓的大步就是指左边$k$的枚举，$k$​每一次自增，对于$a^{km}$而言，都是增加$a^m$；而小步就是指右边$r$的枚举，$r$的每一次自增，对于$ya^r$而言，都是增加$a$​；枚举的步长一个大些，一个小些，但其枚举次数的规模是相同的，这就是大步小步的名字由来。

代码如下：

ll BSGS(ll A, ll B, ll C) {
    A %= C, B %= C;
    mp.clear();
    int m = ceil(sqrt(C*1.0));
    for (int i = 1; i <= m; i ++) {
        B = B * A % C;
        mp[B] = i;
    }
    ll tmp = fpow(A, m, C);
    B = 1;
    for (int i = 1; i <= m; i ++) {
        B = B * tmp % C;
        if (mp.count(B)) 
            return ((ll)i*m - mp[B] + C) % C;
    }
    return -1;
}

2. 拓展BSGS算法

求满足$a^x\equiv y\ (mod\ m)$​的最小自然数x或报告无解，其中$a$​与$m$​不要求互质。
拓展BSGS算法相比于其他拓展算法也显得有些直接，如果$a$与$m$​不互质，那就将其变得互质，而后再使用BSGS算法计算即可。

如何使其变得互质呢，同很多证明方法的第一步一样，先将同余方程变为一半方程，得到

设$d=gcd(a, m)$​​，等式两边同时除$d$​​​，得到

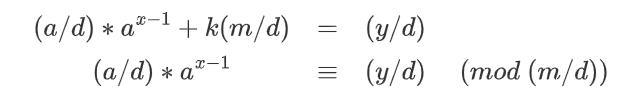
注意如果$y\ \%\ d≠0$，有裴蜀定理得，该式无解。​

以此类推，如果原式$a$与$m/d$​还是不互质，就继续如此操作，直到互质为止，最终就可以得到以下的式子的形式。

$$A*a^{x-k}=C\ (mod\ P)$$

至于左边$A$的处理，可以在枚举左边的时候将其设置为初值进行匹配即可，并不是什么难点，可以结合代码理解。

int exBSGS(int a, int b, int p) {
    a %= p; b %= p;
    if (a == 0) return b > 1 ? -1 : b == 0 && p != 1;
    int c = 0, q = 1;
    while (1) {
        int g = __gcd(a, p);
        if (g == 1) break;
        if (b == q) return c;
        if (b % g) return -1;
        ++c; b /= g; p /= g; q = (ll)a / g * q % p;
    }
    static map<int, int> mp; mp.clear();
    int m = sqrt(p) + 1.5, v = 1;
    for (int i = 1; i <= m; i++) {
        v = (ll)v * a % p;
        mp[(int)((ll)v * b % p)] = i;
    }
    for (int i = 1; i <= m; i++) {
        q = (ll)q * v % p;
        auto it = mp.find(q);
        if (it != mp.end()) return i * m - it->second + c;
    }
    return -1;
}

九、小结

裴蜀定理：有解的条件。

裴蜀定理的有解条件（转化为同余方程的形式之后），实际上是很多定理成立的条件。

乘法逆元：要求互质。但实际上很少有求模数非质数的逆元，即通常会提供更加容易有逆元的条件，当时还是要注意$a$时模数$p$的倍数的情况。

欧拉函数，要求互质。

费马小定理：为质数且互质

BSGS算法：互质

另有借鉴

数论学习笔记1_m0_53373033的博客-CSDN博客

数论学习笔记2_m0_53373033的博客-CSDN博客

数论学习笔记3_m0_53373033的博客-CSDN博客